12.3 角的平分线的性质 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 12.3 角的平分线的性质 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:51:03 | ||
图片预览



文档简介
12.3 角的平分线的性质
任务一 角的平分线的性质
母题1 如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB,求证:AD=CD+AB.
变式练1:如图,∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,求证:PC=PD.
任务二 角的平分线的判定
母题2 如图,在△ABC中,∠ABC的平分线与△ABC的外角∠ACE的平分线交于点P,PD⊥AC于点D,PH⊥BA,交BA的延长线于点H.
(1)若点P到直线BA的距离为5,求点P到直线BC的距离.
(2)求证:点P在∠HAC的平分线上.
变式练2:如图,点A,B在射线OM上,点C,D在射线ON上,已知AB=CD,S△ABP=S△CDP,求证:点P在∠MON的平分线上.
任务三 角平分线的性质与探究性问题
母题3 如图1,在四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
(1)求证:BC=CD.
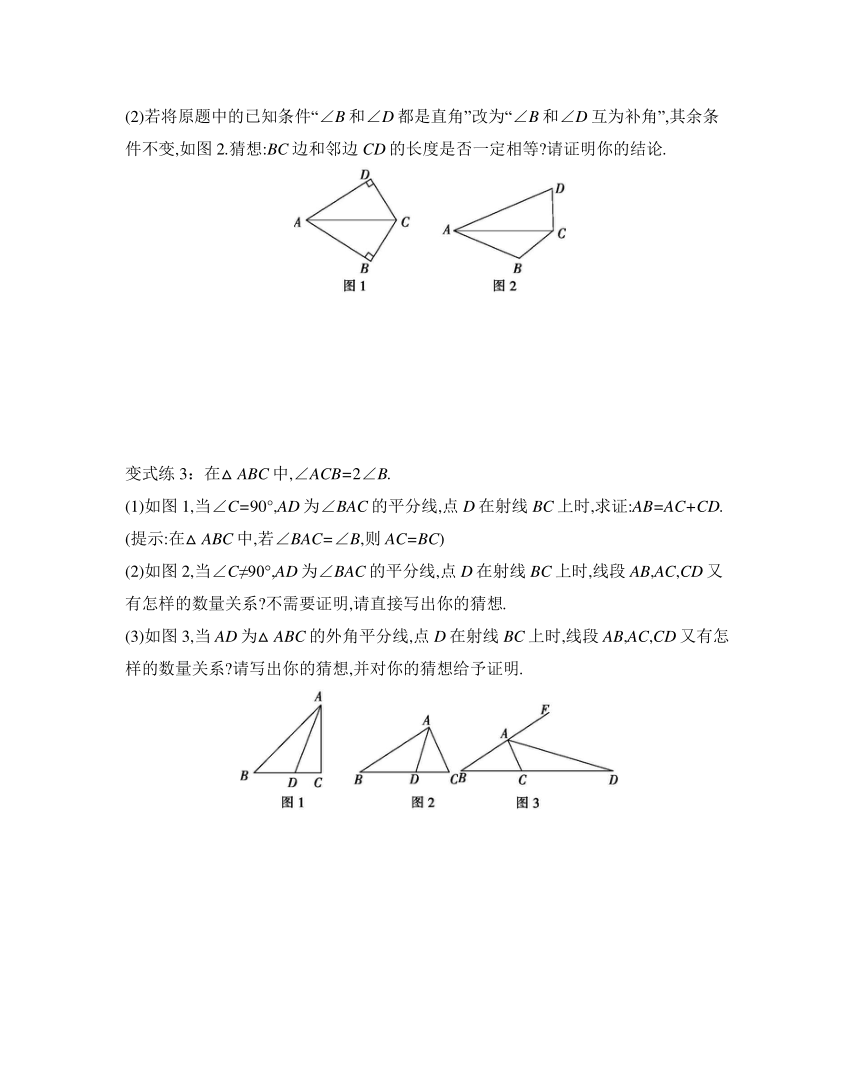
(2)若将原题中的已知条件“∠B和∠D都是直角”改为“∠B和∠D互为补角”,其余条件不变,如图2.猜想:BC边和邻边CD的长度是否一定相等 请证明你的结论.
变式练3:在△ABC中,∠ACB=2∠B.
(1)如图1,当∠C=90°,AD为∠BAC的平分线,点D在射线BC上时,求证:AB=AC+CD.
(提示:在△ABC中,若∠BAC=∠B,则AC=BC)
(2)如图2,当∠C≠90°,AD为∠BAC的平分线,点D在射线BC上时,线段AB,AC,CD又有怎样的数量关系 不需要证明,请直接写出你的猜想.
(3)如图3,当AD为△ABC的外角平分线,点D在射线BC上时,线段AB,AC,CD又有怎样的数量关系 请写出你的猜想,并对你的猜想给予证明.
参考答案
母题1 证明:如图,过点M作ME⊥AD于点E.
∵∠B=∠C=90°,DM平分∠ADC,AM平分∠DAB,
∴∠C=∠DEM=90°,∠B=∠AEM=90°,∠CDM=∠EDM,∠EAM=∠BAM.
在△MCD和△MED中,
∴△MCD≌△MED(AAS),∴CD=DE.
同理,AE=AB,∴AD=DE+AE=CD+AB,
即AD=CD+AB.
变式练1 证明:如图,过点P点作PE⊥OA于点E,PF⊥OB于点F,
∴∠PEC=∠PFD=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°,
而∠PDO+∠PDF=180°,
∴∠PCE=∠PDF.
在△PCE和△PDF中,
∴△PCE≌△PDF(AAS),
∴PC=PD.
母题2 解:(1)如图,过点P作PF⊥BE于点F.
∵点P在∠ABC的平分线上,PH⊥BA,PF⊥BE,
∴PF=PH=5,即点P到直线BC的距离为5.
(2)证明:∵点P在∠ACE的平分线上,PD⊥AC,PF⊥BE,
∴PF=PD.
∵PF=PH,∴PD=PH.
∵PD⊥AC,PH⊥BA,
∴点P在∠HAC的平分线上.
变式练2 证明:如图,过点P作PE⊥OM于点E,PF⊥ON于点F.
∵S△ABP=S△CDP,
∴AB·PE=CD·PF.
∵AB=CD,∴PE=PF,而PE⊥OM,PF⊥ON,
∴点P在∠MON的平分线上.
母题3 解:(1)证明:∵∠D=∠B=90°,
∴CD⊥AD,CB⊥AB.
∵AC平分∠BAD,∴BC=CD.
(2)一定相等.
证明:如图,过点C作CE⊥AD于点E,作CF⊥AB于点F,
∴∠CBF与∠ABC互补.
∵∠ABC和∠D互为补角,
∴∠D=∠CBF.
又∵AC是∠BAD的平分线,∴CE=CF.
在△DCE与△BCF中,
∴△DCE≌△BCF(AAS),
∴BC=CD.
变式练3 解:(1)证明:如图1,过点D作DE⊥AB,交AB于点E.
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED.
∵∠ACB=2∠B,∴∠AED=2∠B.
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,∴BE=DE=DC,
∴AB=BE+AE=CD+AC,即AB=CD+AC.
(2)AB=CD+AC.
提示:如图2,在AB上截取一点G,连接DG,使得AG=AC.
∵AD为∠BAC的平分线,∴∠GAD=∠CAD .
在△ADG和△ADC中,
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB.
∵∠ACB=2∠B,∴∠AGD=2∠B.
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,∴BG=DG=DC,
则AB=BG+AG=CD+AC,
即AB=CD+AC.
(3)AB=CD-AC.
证明:如图3,在AF上截取一点G,使得AG=AC,连接GD.
∵AD为∠FAC的平分线,∴∠GAD=∠CAD.
在△ADG和△ADC中,
∴△ADG≌△ADC(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD.
∵∠ACB=2∠B,∴∠FGD=2∠B.
又∵∠FGD=∠B+∠GDB,∴∠B=∠GDB,
∴BG=DG=DC,
∴AB=BG-AG=CD-AC,即AB=CD-AC.
任务一 角的平分线的性质
母题1 如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB,求证:AD=CD+AB.
变式练1:如图,∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,求证:PC=PD.
任务二 角的平分线的判定
母题2 如图,在△ABC中,∠ABC的平分线与△ABC的外角∠ACE的平分线交于点P,PD⊥AC于点D,PH⊥BA,交BA的延长线于点H.
(1)若点P到直线BA的距离为5,求点P到直线BC的距离.
(2)求证:点P在∠HAC的平分线上.
变式练2:如图,点A,B在射线OM上,点C,D在射线ON上,已知AB=CD,S△ABP=S△CDP,求证:点P在∠MON的平分线上.
任务三 角平分线的性质与探究性问题
母题3 如图1,在四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
(1)求证:BC=CD.
(2)若将原题中的已知条件“∠B和∠D都是直角”改为“∠B和∠D互为补角”,其余条件不变,如图2.猜想:BC边和邻边CD的长度是否一定相等 请证明你的结论.
变式练3:在△ABC中,∠ACB=2∠B.
(1)如图1,当∠C=90°,AD为∠BAC的平分线,点D在射线BC上时,求证:AB=AC+CD.
(提示:在△ABC中,若∠BAC=∠B,则AC=BC)
(2)如图2,当∠C≠90°,AD为∠BAC的平分线,点D在射线BC上时,线段AB,AC,CD又有怎样的数量关系 不需要证明,请直接写出你的猜想.
(3)如图3,当AD为△ABC的外角平分线,点D在射线BC上时,线段AB,AC,CD又有怎样的数量关系 请写出你的猜想,并对你的猜想给予证明.
参考答案
母题1 证明:如图,过点M作ME⊥AD于点E.
∵∠B=∠C=90°,DM平分∠ADC,AM平分∠DAB,
∴∠C=∠DEM=90°,∠B=∠AEM=90°,∠CDM=∠EDM,∠EAM=∠BAM.
在△MCD和△MED中,
∴△MCD≌△MED(AAS),∴CD=DE.
同理,AE=AB,∴AD=DE+AE=CD+AB,
即AD=CD+AB.
变式练1 证明:如图,过点P点作PE⊥OA于点E,PF⊥OB于点F,
∴∠PEC=∠PFD=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°,
而∠PDO+∠PDF=180°,
∴∠PCE=∠PDF.
在△PCE和△PDF中,
∴△PCE≌△PDF(AAS),
∴PC=PD.
母题2 解:(1)如图,过点P作PF⊥BE于点F.
∵点P在∠ABC的平分线上,PH⊥BA,PF⊥BE,
∴PF=PH=5,即点P到直线BC的距离为5.
(2)证明:∵点P在∠ACE的平分线上,PD⊥AC,PF⊥BE,
∴PF=PD.
∵PF=PH,∴PD=PH.
∵PD⊥AC,PH⊥BA,
∴点P在∠HAC的平分线上.
变式练2 证明:如图,过点P作PE⊥OM于点E,PF⊥ON于点F.
∵S△ABP=S△CDP,
∴AB·PE=CD·PF.
∵AB=CD,∴PE=PF,而PE⊥OM,PF⊥ON,
∴点P在∠MON的平分线上.
母题3 解:(1)证明:∵∠D=∠B=90°,
∴CD⊥AD,CB⊥AB.
∵AC平分∠BAD,∴BC=CD.
(2)一定相等.
证明:如图,过点C作CE⊥AD于点E,作CF⊥AB于点F,
∴∠CBF与∠ABC互补.
∵∠ABC和∠D互为补角,
∴∠D=∠CBF.
又∵AC是∠BAD的平分线,∴CE=CF.
在△DCE与△BCF中,
∴△DCE≌△BCF(AAS),
∴BC=CD.
变式练3 解:(1)证明:如图1,过点D作DE⊥AB,交AB于点E.
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED.
∵∠ACB=2∠B,∴∠AED=2∠B.
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,∴BE=DE=DC,
∴AB=BE+AE=CD+AC,即AB=CD+AC.
(2)AB=CD+AC.
提示:如图2,在AB上截取一点G,连接DG,使得AG=AC.
∵AD为∠BAC的平分线,∴∠GAD=∠CAD .
在△ADG和△ADC中,
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB.
∵∠ACB=2∠B,∴∠AGD=2∠B.
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,∴BG=DG=DC,
则AB=BG+AG=CD+AC,
即AB=CD+AC.
(3)AB=CD-AC.
证明:如图3,在AF上截取一点G,使得AG=AC,连接GD.
∵AD为∠FAC的平分线,∴∠GAD=∠CAD.
在△ADG和△ADC中,
∴△ADG≌△ADC(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD.
∵∠ACB=2∠B,∴∠FGD=2∠B.
又∵∠FGD=∠B+∠GDB,∴∠B=∠GDB,
∴BG=DG=DC,
∴AB=BG-AG=CD-AC,即AB=CD-AC.
