13.1 轴对称 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 13.1 轴对称 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 199.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:51:30 | ||
图片预览




文档简介
13.1 轴对称
任务一 轴对称图形性质的应用
子任务1 求面积或周长
母题1 如图,直线AD是△ABC的对称轴,E,F是AD上的任意两点.若△ABC的面积为18 cm2,求图中阴影部分的面积.
变式练1:如图,等边△ABC的边长为10 cm,D、E分别是AB、AC边上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC的外部,则阴影部分图形的周长为 cm.
子任务2 求线段的长
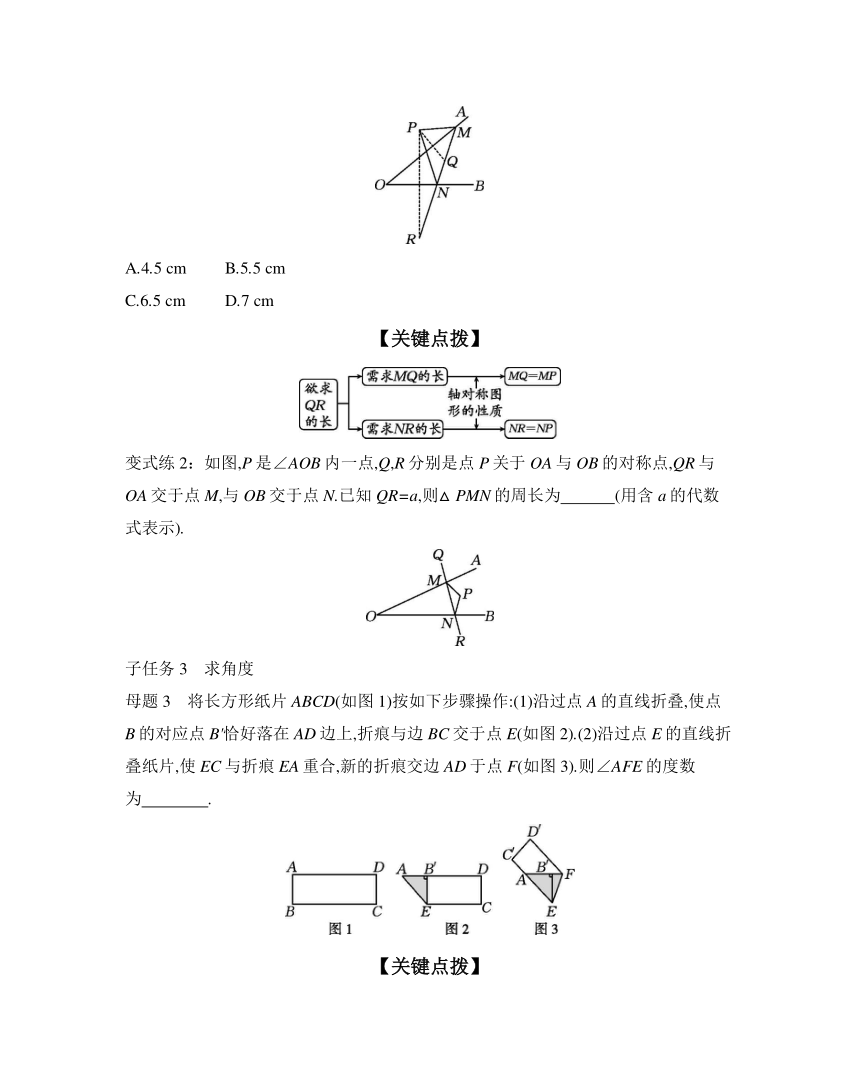
母题2 如图,P是∠AOB外的一点,M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上.点P关于OB的对称点R落在MN的延长线上.若PM=2 cm,PN=3 cm,MN=3.5 cm,则线段QR的长为 ( )
A.4.5 cm B.5.5 cm
C.6.5 cm D.7 cm
【关键点拨】
变式练2:如图,P是∠AOB内一点,Q,R分别是点P关于OA与OB的对称点,QR与OA交于点M,与OB交于点N.已知QR=a,则△PMN的周长为 (用含a的代数式表示).
子任务3 求角度
母题3 将长方形纸片ABCD(如图1)按如下步骤操作:(1)沿过点A的直线折叠,使点B的对应点B'恰好落在AD边上,折痕与边BC交于点E(如图2).(2)沿过点E的直线折叠纸片,使EC与折痕EA重合,新的折痕交边AD于点F(如图3).则∠AFE的度数为 .
【关键点拨】
变式练3:如图1,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在点H、G的位置,再沿BC折叠成图2.
①如图1,若∠DEF=72°,则∠AEG= .
②如图2,若∠DEF=α,则∠GMN= (用α的代数式表示).
任务二 线段垂直平分线的性质的应用
子任务1 求线段的长
母题4 如图,在△ABC中,DE是AC的垂直平分线,AE=3.
(1)若AC=BC,求BC的长.
(2)若△ABD的周长为13,求△ABC的周长.
变式练4:如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12 cm.
(1)求BC的长.
(2)分别连接OA,OB,OC,若△OBC的周长为26 cm,求OA的长.
子任务2 证明线段相等
母题5 如图,在△ABC中,∠ACB的平分线与AB的垂直平分线交于点D,DE⊥AC于点E,DF⊥BC交CB的延长线于点F.
(1)求证:AE=BF.
(2)若AC=24,BC=10,求AE的长.
变式练5:如图,在△ABC中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于点E,并且AB>AC.求证:BE-AC=AE.
参考答案
母题1 解:∵直线AD是△ABC的对称轴,
∴AD⊥BC,BD=CD,
∴AB=AC,
∴阴影部分的面积等于△ABC面积的一半.
∵△ABC的面积为18 cm2,
∴阴影部分的面积=9 cm2.
变式练1 30 提示:将△ADE沿直线DE折叠,点A落在点A'处,
所以AD=A'D,AE=A'E,
则阴影部分图形的周长等于BC+BD+CE+A'D+A'E
=BC+BD+CE+AD+AE
=BC+AB+AC
=30 cm.
母题2 A 提示:∵点P关于OA的对称点Q恰好落在线段MN上.点P关于OB的对称点R落在MN的延长线上,
∴PM=QM,PN=RN.
∵PM=2 cm,PN=3 cm,
∴QM=2(cm),RN=3(cm).
∵MN=3.5 cm,
∴QN=MN-QM=3.5-2=1.5(cm),
∴QR=QN+RN=1.5+3=4.5(cm).故选A.
变式练2 a 提示:
如图,连接PQ,PR.∵Q,R分别是点P关于OA与OB的对称点,
∴OA垂直平分PQ,OB垂直平分PR,
∴PM=QM,PN=RN,
∴△PMN的周长=MN+PM+PN=MN+QM+RN=QR=a.
母题3 67.5° 提示:∵四边形ABCD为矩形,
∴∠BAD=∠ABC=90°,
由折叠的性质得第一次折叠后,题图2中的∠EAB'=∠BAD=45°,∠AB'E=∠ABC=90°,
∴∠AEB'=45°,∠AEC=∠135°.
第二次折叠后,题图3中的∠AEF=∠AEC=67.5°,
∴∠AFE=180°-∠EAB'-∠AEF=180°-45°-67.5°=67.5°.
变式练3 解:①36° 提示:由折叠的性质得∠DEF=∠GEF=72°,
∴∠AEG=180°-72°-72°=36°.
②360°-4x 提示:由折叠的性质得∠GEF=∠DEF=α,∠EFC=∠EFH,∠NMF=∠FMH,∠H=∠N=∠D.
∵四边形ABCD是长方形,
∴AD∥BC,∠D=90°,
∴∠EFM=∠DEF=α.
∵EG∥FH,
∴∠EFH+∠GEF=180°,
∴∠EFH=180°-α,
∴∠MFH=∠EFH-∠EFM=180°-2α.
∵∠H=∠N=∠D=90°,
∴∠FMH=90°-∠MFH=2α-90°,
∴∠NMF=2α-90°,
∴∠GMN=180°-∠FMH-∠NMF=180°-2(2α-90°)=360°-4α.
母题4 解:(1)∵DE是AC的垂直平分线,AE=3,
∴AC=2AE=6,
∴BC=AC=6.
(2)∵DE是AC的垂直平分线,AE=3,
∴AD=DC,AC=2AE=6.
∵△ABD的周长为13,
∴AB+AD+BD=13,
∴AB+CD+BD=13,
即AB+BC=13,
∴△ABC的周长是AB+BC+AC=13+6=19.
变式练4 解:(1)∵l1垂直平分AB,
∴DB=DA.
同理EA=EC,
∴BC=BD+DE+EC=DA+DE+EA=12 cm.
(2)∵l1垂直平分AB,
∴OB=OA.
同理OA=OC,
∴OA=OB=OC.
又∵△OBC的周长为26 cm,BC=12 cm,
∴OB+OC=26-12=14 cm,
∴OB=OC=7 cm,
∴OA=7 cm.
母题5 解:(1)证明:连接AD.如图所示.
∵DM垂直平分线段AB,
∴DA=DB.
∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠DEA=∠DFC=90°.
在Rt△DEA和Rt△DFB中,
∴Rt△DEA≌Rt△DFB(HL),
∴AE=BF.
(2)在Rt△CDE与Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF,
∴AC-AE=BC+BF,
∴24-AE=10+AE,
解得AE=7.
变式练5 证明:
如图,过点D作DG⊥CA交CA的延长线于点G,连接DC,DB.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG,∠GAD=∠EAD,∠AGD=∠AED=90°.
∵DF垂直平分BC,
∴DC=DB.
在Rt△CDG与Rt△BDE中
∴Rt△CDG≌Rt△BDE(HL),
∴CG=BE.
∵在△ADG与△ADE中
∴△ADG≌△ADE(AAS),
∴AG=AE,
∴CG=AG+AC=AE+AC,
∴BE=AE+AC,
∴BE-AC=AE.
任务一 轴对称图形性质的应用
子任务1 求面积或周长
母题1 如图,直线AD是△ABC的对称轴,E,F是AD上的任意两点.若△ABC的面积为18 cm2,求图中阴影部分的面积.
变式练1:如图,等边△ABC的边长为10 cm,D、E分别是AB、AC边上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC的外部,则阴影部分图形的周长为 cm.
子任务2 求线段的长
母题2 如图,P是∠AOB外的一点,M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上.点P关于OB的对称点R落在MN的延长线上.若PM=2 cm,PN=3 cm,MN=3.5 cm,则线段QR的长为 ( )
A.4.5 cm B.5.5 cm
C.6.5 cm D.7 cm
【关键点拨】
变式练2:如图,P是∠AOB内一点,Q,R分别是点P关于OA与OB的对称点,QR与OA交于点M,与OB交于点N.已知QR=a,则△PMN的周长为 (用含a的代数式表示).
子任务3 求角度
母题3 将长方形纸片ABCD(如图1)按如下步骤操作:(1)沿过点A的直线折叠,使点B的对应点B'恰好落在AD边上,折痕与边BC交于点E(如图2).(2)沿过点E的直线折叠纸片,使EC与折痕EA重合,新的折痕交边AD于点F(如图3).则∠AFE的度数为 .
【关键点拨】
变式练3:如图1,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在点H、G的位置,再沿BC折叠成图2.
①如图1,若∠DEF=72°,则∠AEG= .
②如图2,若∠DEF=α,则∠GMN= (用α的代数式表示).
任务二 线段垂直平分线的性质的应用
子任务1 求线段的长
母题4 如图,在△ABC中,DE是AC的垂直平分线,AE=3.
(1)若AC=BC,求BC的长.
(2)若△ABD的周长为13,求△ABC的周长.
变式练4:如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12 cm.
(1)求BC的长.
(2)分别连接OA,OB,OC,若△OBC的周长为26 cm,求OA的长.
子任务2 证明线段相等
母题5 如图,在△ABC中,∠ACB的平分线与AB的垂直平分线交于点D,DE⊥AC于点E,DF⊥BC交CB的延长线于点F.
(1)求证:AE=BF.
(2)若AC=24,BC=10,求AE的长.
变式练5:如图,在△ABC中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于点E,并且AB>AC.求证:BE-AC=AE.
参考答案
母题1 解:∵直线AD是△ABC的对称轴,
∴AD⊥BC,BD=CD,
∴AB=AC,
∴阴影部分的面积等于△ABC面积的一半.
∵△ABC的面积为18 cm2,
∴阴影部分的面积=9 cm2.
变式练1 30 提示:将△ADE沿直线DE折叠,点A落在点A'处,
所以AD=A'D,AE=A'E,
则阴影部分图形的周长等于BC+BD+CE+A'D+A'E
=BC+BD+CE+AD+AE
=BC+AB+AC
=30 cm.
母题2 A 提示:∵点P关于OA的对称点Q恰好落在线段MN上.点P关于OB的对称点R落在MN的延长线上,
∴PM=QM,PN=RN.
∵PM=2 cm,PN=3 cm,
∴QM=2(cm),RN=3(cm).
∵MN=3.5 cm,
∴QN=MN-QM=3.5-2=1.5(cm),
∴QR=QN+RN=1.5+3=4.5(cm).故选A.
变式练2 a 提示:
如图,连接PQ,PR.∵Q,R分别是点P关于OA与OB的对称点,
∴OA垂直平分PQ,OB垂直平分PR,
∴PM=QM,PN=RN,
∴△PMN的周长=MN+PM+PN=MN+QM+RN=QR=a.
母题3 67.5° 提示:∵四边形ABCD为矩形,
∴∠BAD=∠ABC=90°,
由折叠的性质得第一次折叠后,题图2中的∠EAB'=∠BAD=45°,∠AB'E=∠ABC=90°,
∴∠AEB'=45°,∠AEC=∠135°.
第二次折叠后,题图3中的∠AEF=∠AEC=67.5°,
∴∠AFE=180°-∠EAB'-∠AEF=180°-45°-67.5°=67.5°.
变式练3 解:①36° 提示:由折叠的性质得∠DEF=∠GEF=72°,
∴∠AEG=180°-72°-72°=36°.
②360°-4x 提示:由折叠的性质得∠GEF=∠DEF=α,∠EFC=∠EFH,∠NMF=∠FMH,∠H=∠N=∠D.
∵四边形ABCD是长方形,
∴AD∥BC,∠D=90°,
∴∠EFM=∠DEF=α.
∵EG∥FH,
∴∠EFH+∠GEF=180°,
∴∠EFH=180°-α,
∴∠MFH=∠EFH-∠EFM=180°-2α.
∵∠H=∠N=∠D=90°,
∴∠FMH=90°-∠MFH=2α-90°,
∴∠NMF=2α-90°,
∴∠GMN=180°-∠FMH-∠NMF=180°-2(2α-90°)=360°-4α.
母题4 解:(1)∵DE是AC的垂直平分线,AE=3,
∴AC=2AE=6,
∴BC=AC=6.
(2)∵DE是AC的垂直平分线,AE=3,
∴AD=DC,AC=2AE=6.
∵△ABD的周长为13,
∴AB+AD+BD=13,
∴AB+CD+BD=13,
即AB+BC=13,
∴△ABC的周长是AB+BC+AC=13+6=19.
变式练4 解:(1)∵l1垂直平分AB,
∴DB=DA.
同理EA=EC,
∴BC=BD+DE+EC=DA+DE+EA=12 cm.
(2)∵l1垂直平分AB,
∴OB=OA.
同理OA=OC,
∴OA=OB=OC.
又∵△OBC的周长为26 cm,BC=12 cm,
∴OB+OC=26-12=14 cm,
∴OB=OC=7 cm,
∴OA=7 cm.
母题5 解:(1)证明:连接AD.如图所示.
∵DM垂直平分线段AB,
∴DA=DB.
∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠DEA=∠DFC=90°.
在Rt△DEA和Rt△DFB中,
∴Rt△DEA≌Rt△DFB(HL),
∴AE=BF.
(2)在Rt△CDE与Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF,
∴AC-AE=BC+BF,
∴24-AE=10+AE,
解得AE=7.
变式练5 证明:
如图,过点D作DG⊥CA交CA的延长线于点G,连接DC,DB.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG,∠GAD=∠EAD,∠AGD=∠AED=90°.
∵DF垂直平分BC,
∴DC=DB.
在Rt△CDG与Rt△BDE中
∴Rt△CDG≌Rt△BDE(HL),
∴CG=BE.
∵在△ADG与△ADE中
∴△ADG≌△ADE(AAS),
∴AG=AE,
∴CG=AG+AC=AE+AC,
∴BE=AE+AC,
∴BE-AC=AE.
