13.3 等腰三角形 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 13.3 等腰三角形 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 171.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:53:02 | ||
图片预览




文档简介
13.3 等腰三角形
任务一 等腰三角形中的分类讨论问题
子任务1 角的度数的分类讨论问题
母题1 若一个等腰三角形一腰上的高与另一腰的夹角为50°,则顶角的度数为 .
变式练1:在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为60°,则底角的大小为 度.
子任务2 确定等腰三角形的分类讨论问题
母题2 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .
变式练2:在等腰三角形ABC中,∠A为顶角,过点B的一条直线将该等腰三角形分成的两个小三角形均为等腰三角形,则∠A的度数为 .
任务二 利用等边三角形的性质计算
子任务1 求线段的长
母题3 如图,等边三角形ABC的边长为4,D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
变式练3:如图,在边长为1的等边三角形ABC中,D为射线AB上一点,AD=2.点E在射线CB上,且DE=DC,则CE的长为 .
子任务2 计算角度
母题4 如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于 ( )
A.15° B.30°
C.45° D.60°
变式练4:如图,在等边三角形ABC中,AD⊥BC,AD=AC,连接CD并延长,交AB的延长线于点E,求∠E的度数.
任务三 含30 °角的直角三角形的性质的应用
子任务1 求线段长
母题5 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F,BC=6.求CF的长.
变式练4:如图,∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM的长为 ( )
A.3 B.4 C.5 D.6
子任务2 证明线段的倍分关系
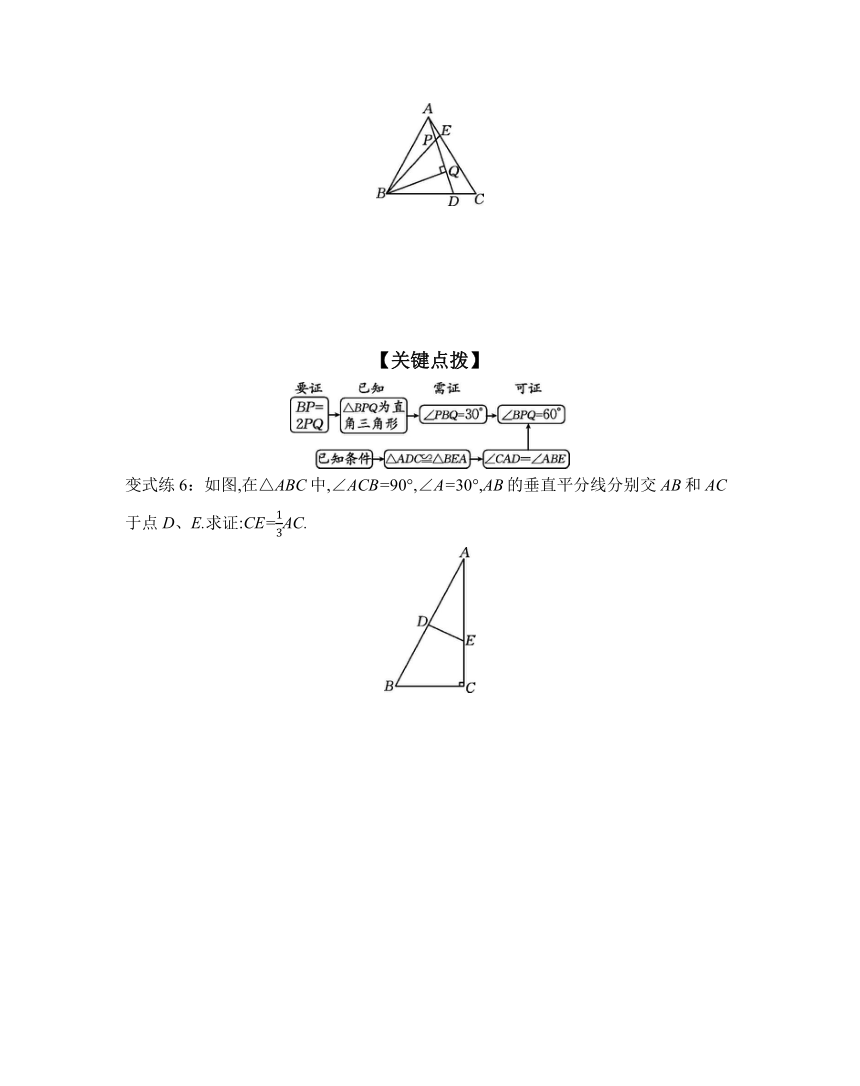
母题6 如图,△ABC是等边三角形,D、E分别为BC、AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q.
(1)求证:△ABE≌△CAD.
(2)求证:BP=2PQ.
【关键点拨】
变式练6:如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D、E.求证:CE=AC.
参考答案
母题1 40°或140° 提示:
①当等腰三角形为锐角三角形时,如图1.
∵∠ABD=50°,BD⊥AC,
∴∠A=90°-50°=40°.
∴三角形的顶角为40°.
②当等腰三角形为钝角三角形时,如图2.
∵∠ABD=50°,BD⊥AC,
∴∠BAD=90°-50°=40°.
∵∠BAD+∠BAC=180°,
∴∠BAC=140°,
∴三角形的顶角为140°.
变式练1 75或15
提示:①当AB的垂直平分线与AC的交点E在线段AC上时,如图1,则∠AED=60°.
图1
∵DE⊥AB,
∴∠A=90°-60°=30°.
∵AB=AC,
∴∠B=∠C==75°.
②当AB的垂直平分线与AC的交点在线段CA的延长线上时,如图2,则∠DEA=60°,
图2
∴∠BAE=90°-60°=30°.
∵AB=AC,
∴∠B=∠C.
∵∠BAE=∠B+∠C,
∴∠B=∠C=15°,
故底角的大小为75°或15°.
母题2 36°或45° 提示:①如图1.
∵AB=AC,BD=AD,AC=CD,
∴∠ABC=∠C=∠BAD,∠CDA=∠CAD.
∵∠CDA=∠ABC+∠BAD=2∠ABC,
∴∠CAB=3∠ABC.
∵∠BAC+∠B+∠C=180°,
∴5∠ABC=180°,
∴∠ABC=36°.
②如图2.
∵AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠ABC.
∵∠BAC+∠B+∠C=180°,
∴4∠ABC=180°,
∴∠ABC=45°.
变式练2 36°或°.
母题3 解:∵△ABC是等边三角形,D是AC的中点,
∴BD平分∠ABC,∠ACB=∠ABC=60°,AC=4,CD=2
∴∠DBE=30°.
∵DE=DB,
∴∠DEB=∠DBE,
∴∠DEB=30°.
∵∠ACB=60°,
∴∠CDE=30°.
∴CE=CD=2.
变式练3 3 提示:
∵△ABC为等边三角形,且边长为1,
∴AB=BC=AC=1,∠ABC=60°,
∴∠EBD=∠ABC=60°.
∵AD=2,
∴BD=AD-AB=2-1=1,
∴BD=BC=1,
∴∠BDC=∠BCD.
∵∠BDC+∠BCD=∠ABC=60°,
∴∠BDC=∠BCD=30°.
∵DE=DC,
∴∠DEB=∠BCD=30°,
∴∠EDB=180°-(∠DEB+∠EBD)=180°-(30°+60°)=90°,
∴BE=2BD=2,
∴CE=BC+BE=1+2=3.
母题4 A 提示:∵在等边三角形ABC中,AD⊥BC,
∴BD=CD,即AD是BC的垂直平分线.
∵点E在AD上,
∴BE=CE,
∴∠EBC=∠ECB.
∵∠EBC=45°,
∴∠ECB=45°.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACE=∠ACB-∠ECB=15°.
故选A.
变式练4 解:∵在等边三角形ABC中,
AB=AC,AD⊥BC,
∴∠CAD=∠BAC.
∵∠BAC=60°,
∴∠CAD=30°.
∵AD=AC,
∴∠ACD=∠ADC.
∵在△ACD中,∠ACD+∠ADC+∠CAD=180°,
∴∠ACD=75°.
∵在△ACE中,∠EAC+∠ACE+∠E=180°,
∴∠E=45°.
母题5 解:连接AF,如图所示.
∵AB=AC,∠BAC=120°,
∴∠B=∠C==30°.
∵AC的垂直平分线EF交AC于点E,交BC于点F,
∴CF=AF,
∴∠FAC=∠C=30°,
∴∠BAF=∠BAC-∠FAC=120°-30°=90°.
在Rt△ABF中,∠B=30°,
∴BF=2AF=2CF,
∴CF=BC=×6=2.
变式练5 C 提示:过点P作PC⊥ON于点C,如图所示.
∵∠AOB=60°,PC⊥ON,
∴∠OPC=90°-60°=30°.
∵OP=12,
∴OC=OP=6.
∵PC⊥ON,PM=PN,MN=2,
∴MC=MN=1,
∴OM=OC-MC=6-1=5.
故选C.
母题6 证明:(1)∵△ABC是等边三角形,
∴AC=AB,∠ACB=∠BAC=60°.
又∵EA=DC,
∴△ABE≌△CAD(SAS).
(2)∵△ABE≌△CAD,
∴∠EBA=∠DAC.
∵∠BAD+∠CAD=∠BAC=60°,
∴∠DAB+∠EBA=60°.
∵∠QPB=∠DAB+∠EBA,
∴∠QPB=60°.
∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=90°-∠BPQ=90°-60°=30°,
∴BP=2PQ.
变式练6 证明:连接BE,如图所示.
∵DE为AB边的垂直平分线,
∴BE=AE.
∵∠A=30°,∠ACB=90°,
∴∠ABC=60°,
∴∠EBA=∠A=30°.
在Rt△BCE中,∠EBC=∠ABC-∠EBA=30°,
∴EC=BE=AE,
∴CE=AC.
任务一 等腰三角形中的分类讨论问题
子任务1 角的度数的分类讨论问题
母题1 若一个等腰三角形一腰上的高与另一腰的夹角为50°,则顶角的度数为 .
变式练1:在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为60°,则底角的大小为 度.
子任务2 确定等腰三角形的分类讨论问题
母题2 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .
变式练2:在等腰三角形ABC中,∠A为顶角,过点B的一条直线将该等腰三角形分成的两个小三角形均为等腰三角形,则∠A的度数为 .
任务二 利用等边三角形的性质计算
子任务1 求线段的长
母题3 如图,等边三角形ABC的边长为4,D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
变式练3:如图,在边长为1的等边三角形ABC中,D为射线AB上一点,AD=2.点E在射线CB上,且DE=DC,则CE的长为 .
子任务2 计算角度
母题4 如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于 ( )
A.15° B.30°
C.45° D.60°
变式练4:如图,在等边三角形ABC中,AD⊥BC,AD=AC,连接CD并延长,交AB的延长线于点E,求∠E的度数.
任务三 含30 °角的直角三角形的性质的应用
子任务1 求线段长
母题5 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F,BC=6.求CF的长.
变式练4:如图,∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM的长为 ( )
A.3 B.4 C.5 D.6
子任务2 证明线段的倍分关系
母题6 如图,△ABC是等边三角形,D、E分别为BC、AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q.
(1)求证:△ABE≌△CAD.
(2)求证:BP=2PQ.
【关键点拨】
变式练6:如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D、E.求证:CE=AC.
参考答案
母题1 40°或140° 提示:
①当等腰三角形为锐角三角形时,如图1.
∵∠ABD=50°,BD⊥AC,
∴∠A=90°-50°=40°.
∴三角形的顶角为40°.
②当等腰三角形为钝角三角形时,如图2.
∵∠ABD=50°,BD⊥AC,
∴∠BAD=90°-50°=40°.
∵∠BAD+∠BAC=180°,
∴∠BAC=140°,
∴三角形的顶角为140°.
变式练1 75或15
提示:①当AB的垂直平分线与AC的交点E在线段AC上时,如图1,则∠AED=60°.
图1
∵DE⊥AB,
∴∠A=90°-60°=30°.
∵AB=AC,
∴∠B=∠C==75°.
②当AB的垂直平分线与AC的交点在线段CA的延长线上时,如图2,则∠DEA=60°,
图2
∴∠BAE=90°-60°=30°.
∵AB=AC,
∴∠B=∠C.
∵∠BAE=∠B+∠C,
∴∠B=∠C=15°,
故底角的大小为75°或15°.
母题2 36°或45° 提示:①如图1.
∵AB=AC,BD=AD,AC=CD,
∴∠ABC=∠C=∠BAD,∠CDA=∠CAD.
∵∠CDA=∠ABC+∠BAD=2∠ABC,
∴∠CAB=3∠ABC.
∵∠BAC+∠B+∠C=180°,
∴5∠ABC=180°,
∴∠ABC=36°.
②如图2.
∵AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠ABC.
∵∠BAC+∠B+∠C=180°,
∴4∠ABC=180°,
∴∠ABC=45°.
变式练2 36°或°.
母题3 解:∵△ABC是等边三角形,D是AC的中点,
∴BD平分∠ABC,∠ACB=∠ABC=60°,AC=4,CD=2
∴∠DBE=30°.
∵DE=DB,
∴∠DEB=∠DBE,
∴∠DEB=30°.
∵∠ACB=60°,
∴∠CDE=30°.
∴CE=CD=2.
变式练3 3 提示:
∵△ABC为等边三角形,且边长为1,
∴AB=BC=AC=1,∠ABC=60°,
∴∠EBD=∠ABC=60°.
∵AD=2,
∴BD=AD-AB=2-1=1,
∴BD=BC=1,
∴∠BDC=∠BCD.
∵∠BDC+∠BCD=∠ABC=60°,
∴∠BDC=∠BCD=30°.
∵DE=DC,
∴∠DEB=∠BCD=30°,
∴∠EDB=180°-(∠DEB+∠EBD)=180°-(30°+60°)=90°,
∴BE=2BD=2,
∴CE=BC+BE=1+2=3.
母题4 A 提示:∵在等边三角形ABC中,AD⊥BC,
∴BD=CD,即AD是BC的垂直平分线.
∵点E在AD上,
∴BE=CE,
∴∠EBC=∠ECB.
∵∠EBC=45°,
∴∠ECB=45°.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACE=∠ACB-∠ECB=15°.
故选A.
变式练4 解:∵在等边三角形ABC中,
AB=AC,AD⊥BC,
∴∠CAD=∠BAC.
∵∠BAC=60°,
∴∠CAD=30°.
∵AD=AC,
∴∠ACD=∠ADC.
∵在△ACD中,∠ACD+∠ADC+∠CAD=180°,
∴∠ACD=75°.
∵在△ACE中,∠EAC+∠ACE+∠E=180°,
∴∠E=45°.
母题5 解:连接AF,如图所示.
∵AB=AC,∠BAC=120°,
∴∠B=∠C==30°.
∵AC的垂直平分线EF交AC于点E,交BC于点F,
∴CF=AF,
∴∠FAC=∠C=30°,
∴∠BAF=∠BAC-∠FAC=120°-30°=90°.
在Rt△ABF中,∠B=30°,
∴BF=2AF=2CF,
∴CF=BC=×6=2.
变式练5 C 提示:过点P作PC⊥ON于点C,如图所示.
∵∠AOB=60°,PC⊥ON,
∴∠OPC=90°-60°=30°.
∵OP=12,
∴OC=OP=6.
∵PC⊥ON,PM=PN,MN=2,
∴MC=MN=1,
∴OM=OC-MC=6-1=5.
故选C.
母题6 证明:(1)∵△ABC是等边三角形,
∴AC=AB,∠ACB=∠BAC=60°.
又∵EA=DC,
∴△ABE≌△CAD(SAS).
(2)∵△ABE≌△CAD,
∴∠EBA=∠DAC.
∵∠BAD+∠CAD=∠BAC=60°,
∴∠DAB+∠EBA=60°.
∵∠QPB=∠DAB+∠EBA,
∴∠QPB=60°.
∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=90°-∠BPQ=90°-60°=30°,
∴BP=2PQ.
变式练6 证明:连接BE,如图所示.
∵DE为AB边的垂直平分线,
∴BE=AE.
∵∠A=30°,∠ACB=90°,
∴∠ABC=60°,
∴∠EBA=∠A=30°.
在Rt△BCE中,∠EBC=∠ABC-∠EBA=30°,
∴EC=BE=AE,
∴CE=AC.
