13.4 课题学习 最短路径问题 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 13.4 课题学习 最短路径问题 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 | 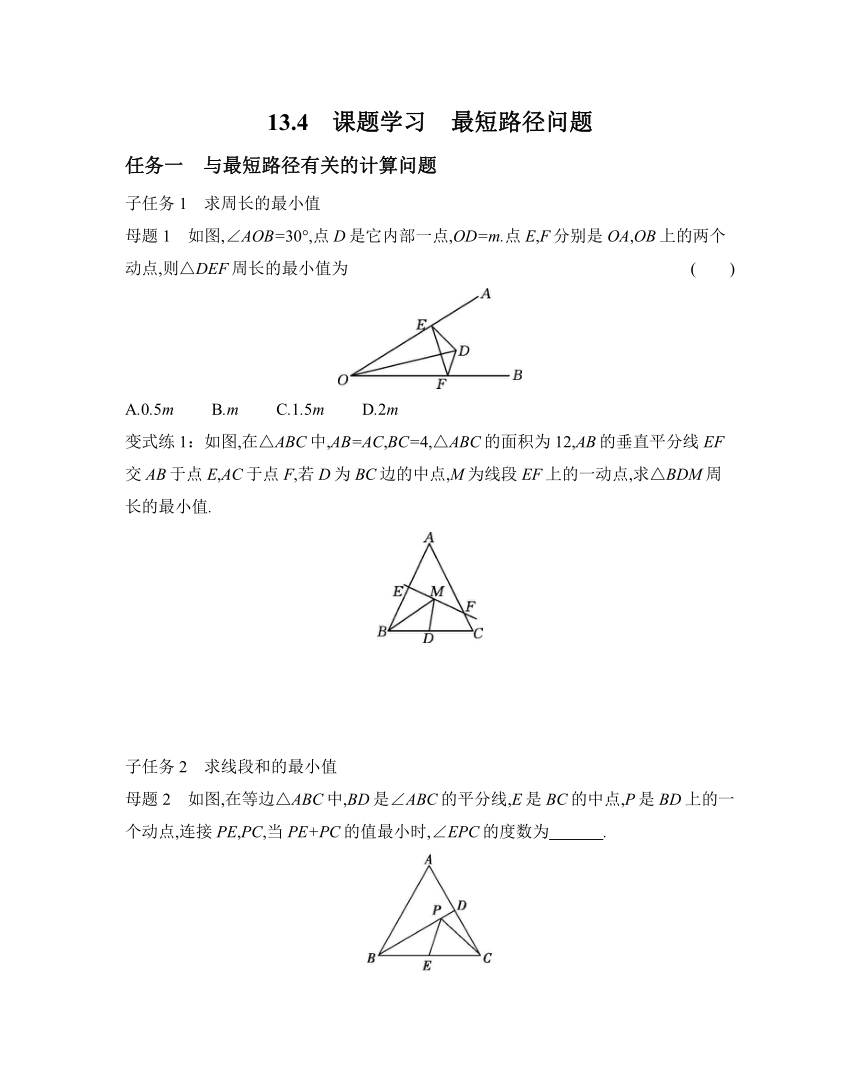 | |
| 格式 | docx | ||
| 文件大小 | 113.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:53:15 | ||
图片预览

文档简介
13.4 课题学习 最短路径问题
任务一 与最短路径有关的计算问题
子任务1 求周长的最小值
母题1 如图,∠AOB=30°,点D是它内部一点,OD=m.点E,F分别是OA,OB上的两个动点,则△DEF周长的最小值为 ( )
A.0.5m B.m C.1.5m D.2m
变式练1:如图,在△ABC中,AB=AC,BC=4,△ABC的面积为12,AB的垂直平分线EF交AB于点E,AC于点F,若D为BC边的中点,M为线段EF上的一动点,求△BDM周长的最小值.
子任务2 求线段和的最小值
母题2 如图,在等边△ABC中,BD是∠ABC的平分线,E是BC的中点,P是BD上的一个动点,连接PE,PC,当PE+PC的值最小时,∠EPC的度数为 .
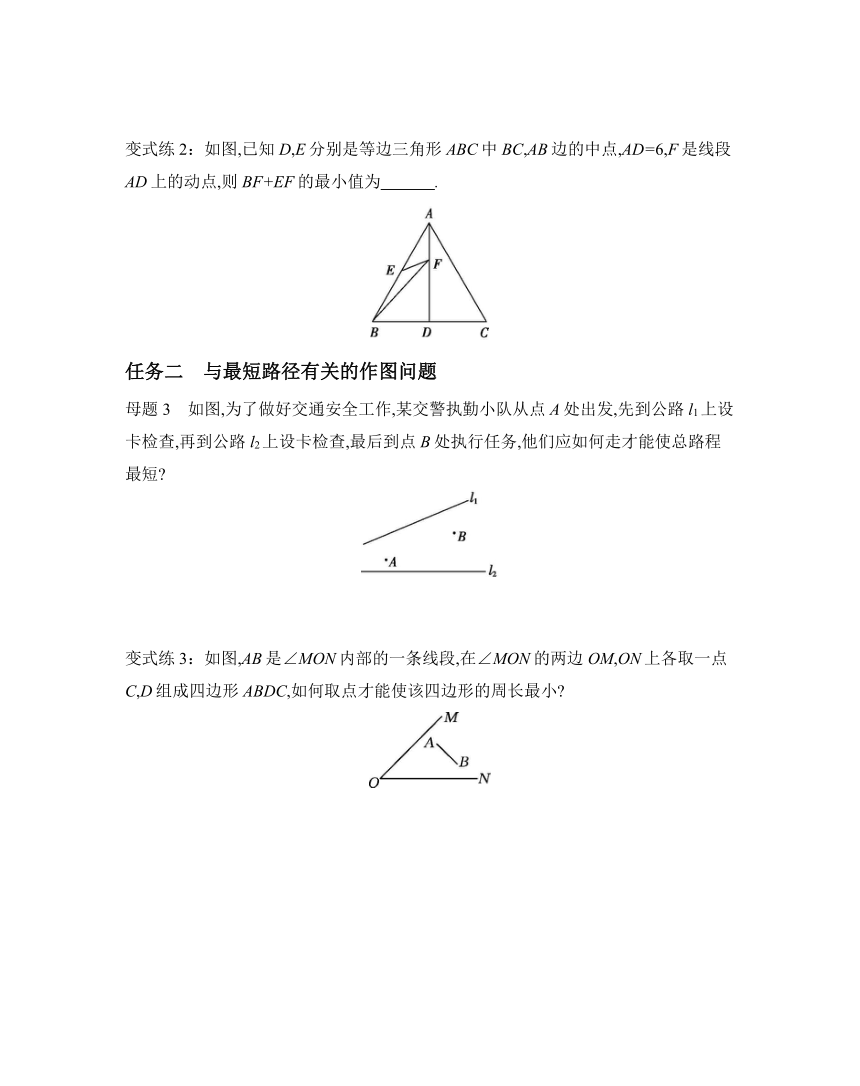
变式练2:如图,已知D,E分别是等边三角形ABC中BC,AB边的中点,AD=6,F是线段AD上的动点,则BF+EF的最小值为 .
任务二 与最短路径有关的作图问题
母题3 如图,为了做好交通安全工作,某交警执勤小队从点A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后到点B处执行任务,他们应如何走才能使总路程最短
变式练3:如图,AB是∠MON内部的一条线段,在∠MON的两边OM,ON上各取一点C,D组成四边形ABDC,如何取点才能使该四边形的周长最小
参考答案
母题1 B 提示:如图,作D点关于AO的对称点G,作D点关于OB的对称点H,连接GH交AO于点E,交OB于点F,连接GO,OH,
由对称性可知,GE=ED,DF=FH,OG=OD=OH,
∴ED+DF+EF=GE+EF+FH=GH,
此时△DEF的周长最小,最小值为GH.
∵∠GOA=∠AOD,∠DOB=∠BOH,
∴∠GOH=2∠AOB.
∵∠AOB=30°,
∴∠GOH=60°,
∴△GOH是等边三角形,
∴GH=OH=OD.
∵DO=m,
∴△DEF周长的最小值为m.
故选B.
变式练1 解:如图,连接AD、AM.
∵△ABC是等腰三角形,点D是底边BC边的中点,
∴AD⊥BC,BD=CD=2,
∴S△ABC=BC·AD=×4×AD=12,
解得AD=6.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,AM=BM,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最小值=(BM+MD)+BD=AD+BC=6+×4=6+2=8.
母题2 60°
变式练2 6
母题3 解:(1)如图,作点A关于直线l1的对称点A'.
(2)作点B关于直线l2的对称点B'.
(3)连接A'B',分别交直线l1,l2于点C,D,连接AC,BD.
所以先到点C处设卡检查,再到点D处设卡检查,最后到点B处执行任务,按照这样的路线所走的路程最短.
变式练3 解:
如图,作点A关于OM的对称点E,再作点B关于ON的对称点F,连接EF交OM于点C,交ON于点D,连接AC,CD,BD,
则四边形ABDC即所求.
任务一 与最短路径有关的计算问题
子任务1 求周长的最小值
母题1 如图,∠AOB=30°,点D是它内部一点,OD=m.点E,F分别是OA,OB上的两个动点,则△DEF周长的最小值为 ( )
A.0.5m B.m C.1.5m D.2m
变式练1:如图,在△ABC中,AB=AC,BC=4,△ABC的面积为12,AB的垂直平分线EF交AB于点E,AC于点F,若D为BC边的中点,M为线段EF上的一动点,求△BDM周长的最小值.
子任务2 求线段和的最小值
母题2 如图,在等边△ABC中,BD是∠ABC的平分线,E是BC的中点,P是BD上的一个动点,连接PE,PC,当PE+PC的值最小时,∠EPC的度数为 .
变式练2:如图,已知D,E分别是等边三角形ABC中BC,AB边的中点,AD=6,F是线段AD上的动点,则BF+EF的最小值为 .
任务二 与最短路径有关的作图问题
母题3 如图,为了做好交通安全工作,某交警执勤小队从点A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后到点B处执行任务,他们应如何走才能使总路程最短
变式练3:如图,AB是∠MON内部的一条线段,在∠MON的两边OM,ON上各取一点C,D组成四边形ABDC,如何取点才能使该四边形的周长最小
参考答案
母题1 B 提示:如图,作D点关于AO的对称点G,作D点关于OB的对称点H,连接GH交AO于点E,交OB于点F,连接GO,OH,
由对称性可知,GE=ED,DF=FH,OG=OD=OH,
∴ED+DF+EF=GE+EF+FH=GH,
此时△DEF的周长最小,最小值为GH.
∵∠GOA=∠AOD,∠DOB=∠BOH,
∴∠GOH=2∠AOB.
∵∠AOB=30°,
∴∠GOH=60°,
∴△GOH是等边三角形,
∴GH=OH=OD.
∵DO=m,
∴△DEF周长的最小值为m.
故选B.
变式练1 解:如图,连接AD、AM.
∵△ABC是等腰三角形,点D是底边BC边的中点,
∴AD⊥BC,BD=CD=2,
∴S△ABC=BC·AD=×4×AD=12,
解得AD=6.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,AM=BM,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最小值=(BM+MD)+BD=AD+BC=6+×4=6+2=8.
母题2 60°
变式练2 6
母题3 解:(1)如图,作点A关于直线l1的对称点A'.
(2)作点B关于直线l2的对称点B'.
(3)连接A'B',分别交直线l1,l2于点C,D,连接AC,BD.
所以先到点C处设卡检查,再到点D处设卡检查,最后到点B处执行任务,按照这样的路线所走的路程最短.
变式练3 解:
如图,作点A关于OM的对称点E,再作点B关于ON的对称点F,连接EF交OM于点C,交ON于点D,连接AC,CD,BD,
则四边形ABDC即所求.
