14.2 乘法公式 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 14.2 乘法公式 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 30.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:54:22 | ||
图片预览


文档简介
14.2 乘法公式
任务一 平方差公式的运用
母题1 计算:(2a+3b)(3b-2a).
变式练1:计算:(2x-y)(y+2x)-(2y+x)(2y-x).
任务二 完全平方公式的运用
母题2 计算:(2x-3)2.
变式练2:计算(3x+y)2+(x+3y)2的值.
任务三 乘法公式整体的运用
母题3 计算:(a-b+c)2.
变式练3:计算:(2x-y+3)2.
任务四 巧用平方差公式计算
母题4 计算(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1).老师讲解的方法如下:
解:原式=(22-1)(22+1)(24+1)(28+1)(216+1)(232+1)
=(24-1)(24+1)(28+1)(216+1)(232+1)
=(28-1)(28+1)(216+1)(232+1)
=264-1.
方法应用
按照上述方法计算(3-1)(3+1)(32+1)·(34+1)(38+1)(316+1)(332+1)(364+1).
变式练4:计算:2(3+1)(32+1)(34+1)(38+1)+1.
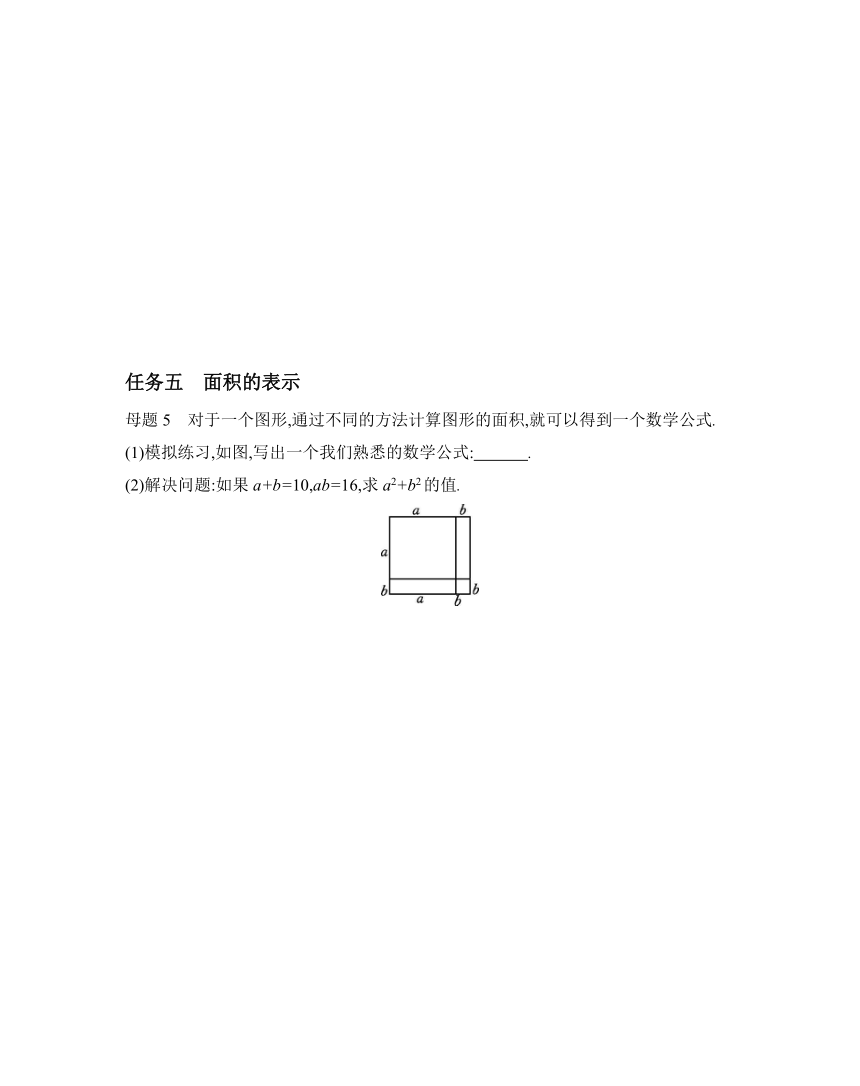
任务五 面积的表示
母题5 对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学公式.
(1)模拟练习,如图,写出一个我们熟悉的数学公式: .
(2)解决问题:如果a+b=10,ab=16,求a2+b2的值.
变式练5:如图,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.
(1)通过计算两个图形的面积(阴影部分的面积),可以验证的等式是 .
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
D.a2-b2=(a-b)2
(2)应用你从(1)中选出的等式,完成下题:
已知a+b=7,a2-b2=28,求a-b的值.
参考答案
母题1 解:原式=(3b+2a)(3b-2a)
=(3b)2-(2a)2
=9b2-4a2.
变式练1 解:原式=4x2-y2-(4y2-x2)=4x2-y2-4y2+x2=5x2-5y2.
母题2 解:原式=(2x)2-2·(2x)·3+32
=4x2-12x+9.
变式练2 解:原式=9x2+6xy+y2+x2+6xy+9y2
=10x2+12xy+10y2.
母题3 解:原式=[a+(c-b)]2
=a2+2a(c-b)+(c-b)2
=a2+b2+c2-2ab+2ac-2bc.
变式练3 解:原式=[(2x-y)+3]2
=(2x-y)2+2(2x-y)·3+32
=4x2-4xy+y2+12x-6y+9.
母题4 解:原式=(32-1)(32+1)(34+1)·(38+1)(316+1)(332+1)(364+1)
=(364-1)(364+1)
=3128-1.
变式练4 解:2(3+1)(32+1)(34+1)(38+1)+1
=(3-1)(3+1)(32+1)(34+1)(38+1)+1
=(32-1)(32+1)(34+1)(38+1)+1
=(34-1)(34+1)(38+1)+1
=(38-1)(38+1)+1
=316-1+1
=316.
母题5 解:(1)(a+b)2=a2+2ab+b2.
(2)∵(a+b)2=a2+2ab+b2,a+b=10,ab=16,
∴a2+b2=(a+b)2-2ab=102-2×16=68.
变式练5 解:(1)B
(2)∵a+b=7,a2-b2=28,
由(1)知a2-b2=(a+b)(a-b),
∴28=7(a-b),
∴a-b=4.
任务一 平方差公式的运用
母题1 计算:(2a+3b)(3b-2a).
变式练1:计算:(2x-y)(y+2x)-(2y+x)(2y-x).
任务二 完全平方公式的运用
母题2 计算:(2x-3)2.
变式练2:计算(3x+y)2+(x+3y)2的值.
任务三 乘法公式整体的运用
母题3 计算:(a-b+c)2.
变式练3:计算:(2x-y+3)2.
任务四 巧用平方差公式计算
母题4 计算(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1).老师讲解的方法如下:
解:原式=(22-1)(22+1)(24+1)(28+1)(216+1)(232+1)
=(24-1)(24+1)(28+1)(216+1)(232+1)
=(28-1)(28+1)(216+1)(232+1)
=264-1.
方法应用
按照上述方法计算(3-1)(3+1)(32+1)·(34+1)(38+1)(316+1)(332+1)(364+1).
变式练4:计算:2(3+1)(32+1)(34+1)(38+1)+1.
任务五 面积的表示
母题5 对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学公式.
(1)模拟练习,如图,写出一个我们熟悉的数学公式: .
(2)解决问题:如果a+b=10,ab=16,求a2+b2的值.
变式练5:如图,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.
(1)通过计算两个图形的面积(阴影部分的面积),可以验证的等式是 .
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
D.a2-b2=(a-b)2
(2)应用你从(1)中选出的等式,完成下题:
已知a+b=7,a2-b2=28,求a-b的值.
参考答案
母题1 解:原式=(3b+2a)(3b-2a)
=(3b)2-(2a)2
=9b2-4a2.
变式练1 解:原式=4x2-y2-(4y2-x2)=4x2-y2-4y2+x2=5x2-5y2.
母题2 解:原式=(2x)2-2·(2x)·3+32
=4x2-12x+9.
变式练2 解:原式=9x2+6xy+y2+x2+6xy+9y2
=10x2+12xy+10y2.
母题3 解:原式=[a+(c-b)]2
=a2+2a(c-b)+(c-b)2
=a2+b2+c2-2ab+2ac-2bc.
变式练3 解:原式=[(2x-y)+3]2
=(2x-y)2+2(2x-y)·3+32
=4x2-4xy+y2+12x-6y+9.
母题4 解:原式=(32-1)(32+1)(34+1)·(38+1)(316+1)(332+1)(364+1)
=(364-1)(364+1)
=3128-1.
变式练4 解:2(3+1)(32+1)(34+1)(38+1)+1
=(3-1)(3+1)(32+1)(34+1)(38+1)+1
=(32-1)(32+1)(34+1)(38+1)+1
=(34-1)(34+1)(38+1)+1
=(38-1)(38+1)+1
=316-1+1
=316.
母题5 解:(1)(a+b)2=a2+2ab+b2.
(2)∵(a+b)2=a2+2ab+b2,a+b=10,ab=16,
∴a2+b2=(a+b)2-2ab=102-2×16=68.
变式练5 解:(1)B
(2)∵a+b=7,a2-b2=28,
由(1)知a2-b2=(a+b)(a-b),
∴28=7(a-b),
∴a-b=4.
