7.4.2二项式系数的性质及应用(同步测试)(含解析)-高中数学苏教版(2019)选择性必修2
文档属性
| 名称 | 7.4.2二项式系数的性质及应用(同步测试)(含解析)-高中数学苏教版(2019)选择性必修2 |

|
|
| 格式 | doc | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览

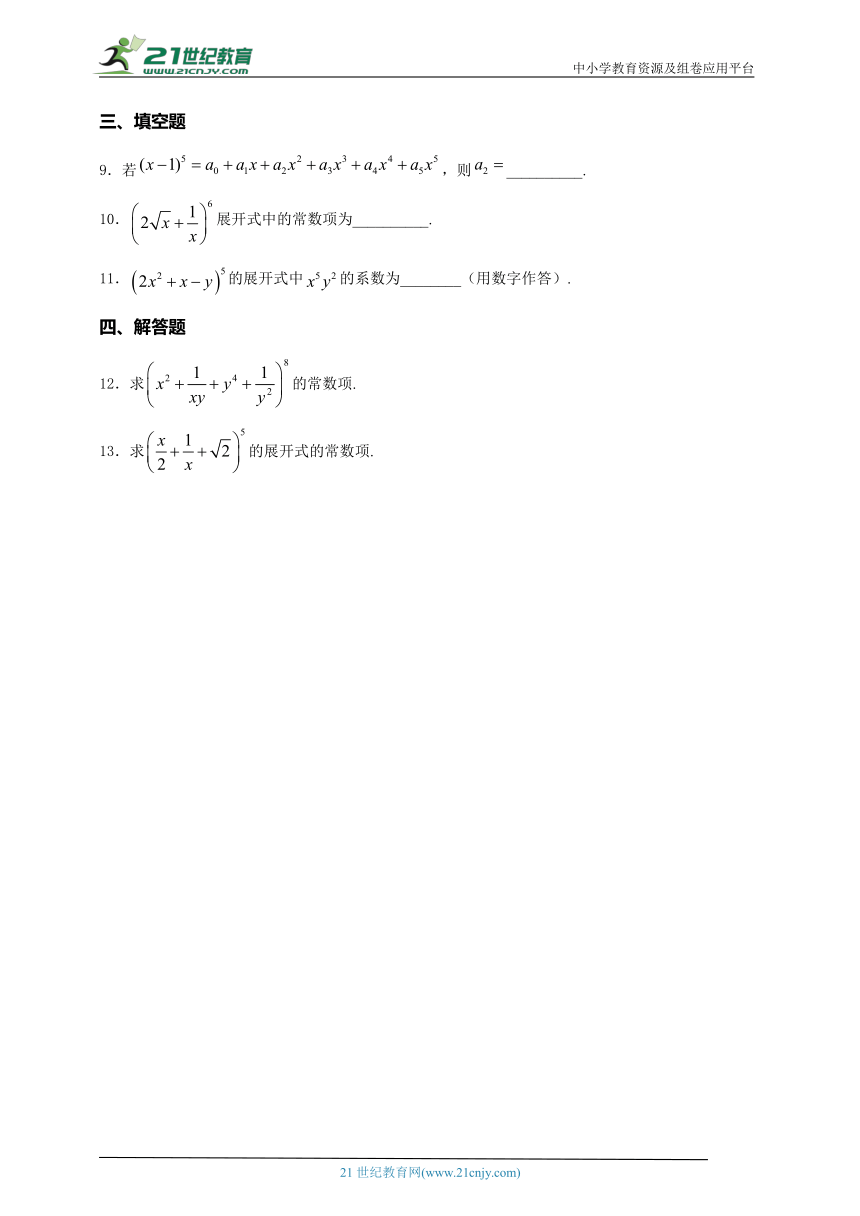

文档简介
中小学教育资源及组卷应用平台
7.4.2二项式系数的性质及应用(同步测试)-高中数学苏教版(2019)选择性必修2
一、选择题
1.的展开式中的系数为( )
A.80 B.40 C.10 D.
2.的展开式中的系数为( )
A.-60 B.-30 C.30 D.60
3.已知,则( )
A. B.0 C.1 D.-1
4.若展开式中只有第7项的二项式系数最大,则( )
A.9 B.10 C.11 D.12
5.数列的最大项为第k项,则( )
A.4或5 B.5 C.5或6 D.6
6.若展开式的二项式系数之和为64,则展开式的常数项为( )
A.10 B.20 C.30 D.120
二、多项选择题
7.已知二项式的展开式共有8项,则下列说法正确的有( )
A.所有项的二项式系数和为128 B.所有项的系数和为1
C.二项式系数最大的项为第5项 D.有理项共有3项
8.的展开式中含有项的系数为( )
A.10 B.-10 C.20 D.-20
三、填空题
9.若,则__________.
10.展开式中的常数项为__________.
11.的展开式中的系数为________(用数字作答).
四、解答题
12.求的常数项.
13.求的展开式的常数项.
参考答案
1.答案:B
解析:由二项式展开式的通项公式为,
令,可得,
所以展开式中的系数为.
故选:B.
2.答案:B
解析:,根据二项式的展开式,
令时,的展开式满足关系式为,
当时,的展开式的系数为,
故展开式中的系数为.
3.答案:D
解析:因为,
取时,可得,
令,可得,
所以.
故选:D.
4.答案:D
解析:由的展开式中只有第7项的二项式系数最大,得展开式共有13项,
所以.
故选:D.
5.答案:C
解析:令,则,则.
故当时,数列单调递增;当时,数列单调递增;当时,数列递减,所以第5或第6项是数列的最大项,故选C.
6.答案:B
解析:根据题意可得,解得,
则展开式的通项为,令,得,
所以常数项为:,
故选:B.
7.答案:AB
解析:因为二项式的展开式共有8项,所以.对于选项A,所有项的二项式系数和为,故A正确.对于选项B,令,则,所以所有项的系数和为1,故B正确.对于选项C,由题意,得二项式系数最大的项为第4项和第5项,故C不正确.对于选项D,二项展开式的通项,当时,二项展开式中对应的项均为有理项,所以有理项有4项,故D不正确.选AB.
8.答案:B
解析:,故的展开式中含有项的系数为-10.
9.答案:
解析:的展开式通项是:,
依题意得,,即,所以,
故答案为:
10.答案:240
解析:展开式的通项公式为,
令得,,
故答案为:240.
11.答案:120
解析:由于,
所以的展开式中含的项为,
所以的展开式中的系数为120.
故答案为:120
12.答案:1680
解析:由题意可知,常数项的构成必为,
故常数项为.
13.答案:
解析:方法一:由二项式定理得
其中为常数项的有
中的第3项:;
中的第2项:;
展开式的最后1项:.
综上可知,常数项为.
方法二:原式.
求原式中展开式的常数项,等价于求的展开式中含的项的系数,即.
所以所求的常数项为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
7.4.2二项式系数的性质及应用(同步测试)-高中数学苏教版(2019)选择性必修2
一、选择题
1.的展开式中的系数为( )
A.80 B.40 C.10 D.
2.的展开式中的系数为( )
A.-60 B.-30 C.30 D.60
3.已知,则( )
A. B.0 C.1 D.-1
4.若展开式中只有第7项的二项式系数最大,则( )
A.9 B.10 C.11 D.12
5.数列的最大项为第k项,则( )
A.4或5 B.5 C.5或6 D.6
6.若展开式的二项式系数之和为64,则展开式的常数项为( )
A.10 B.20 C.30 D.120
二、多项选择题
7.已知二项式的展开式共有8项,则下列说法正确的有( )
A.所有项的二项式系数和为128 B.所有项的系数和为1
C.二项式系数最大的项为第5项 D.有理项共有3项
8.的展开式中含有项的系数为( )
A.10 B.-10 C.20 D.-20
三、填空题
9.若,则__________.
10.展开式中的常数项为__________.
11.的展开式中的系数为________(用数字作答).
四、解答题
12.求的常数项.
13.求的展开式的常数项.
参考答案
1.答案:B
解析:由二项式展开式的通项公式为,
令,可得,
所以展开式中的系数为.
故选:B.
2.答案:B
解析:,根据二项式的展开式,
令时,的展开式满足关系式为,
当时,的展开式的系数为,
故展开式中的系数为.
3.答案:D
解析:因为,
取时,可得,
令,可得,
所以.
故选:D.
4.答案:D
解析:由的展开式中只有第7项的二项式系数最大,得展开式共有13项,
所以.
故选:D.
5.答案:C
解析:令,则,则.
故当时,数列单调递增;当时,数列单调递增;当时,数列递减,所以第5或第6项是数列的最大项,故选C.
6.答案:B
解析:根据题意可得,解得,
则展开式的通项为,令,得,
所以常数项为:,
故选:B.
7.答案:AB
解析:因为二项式的展开式共有8项,所以.对于选项A,所有项的二项式系数和为,故A正确.对于选项B,令,则,所以所有项的系数和为1,故B正确.对于选项C,由题意,得二项式系数最大的项为第4项和第5项,故C不正确.对于选项D,二项展开式的通项,当时,二项展开式中对应的项均为有理项,所以有理项有4项,故D不正确.选AB.
8.答案:B
解析:,故的展开式中含有项的系数为-10.
9.答案:
解析:的展开式通项是:,
依题意得,,即,所以,
故答案为:
10.答案:240
解析:展开式的通项公式为,
令得,,
故答案为:240.
11.答案:120
解析:由于,
所以的展开式中含的项为,
所以的展开式中的系数为120.
故答案为:120
12.答案:1680
解析:由题意可知,常数项的构成必为,
故常数项为.
13.答案:
解析:方法一:由二项式定理得
其中为常数项的有
中的第3项:;
中的第2项:;
展开式的最后1项:.
综上可知,常数项为.
方法二:原式.
求原式中展开式的常数项,等价于求的展开式中含的项的系数,即.
所以所求的常数项为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
