9.1 线性回归分分析(同步测试)(含解析)-高中数学苏教版(2019)选择性必修2
文档属性
| 名称 | 9.1 线性回归分分析(同步测试)(含解析)-高中数学苏教版(2019)选择性必修2 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览


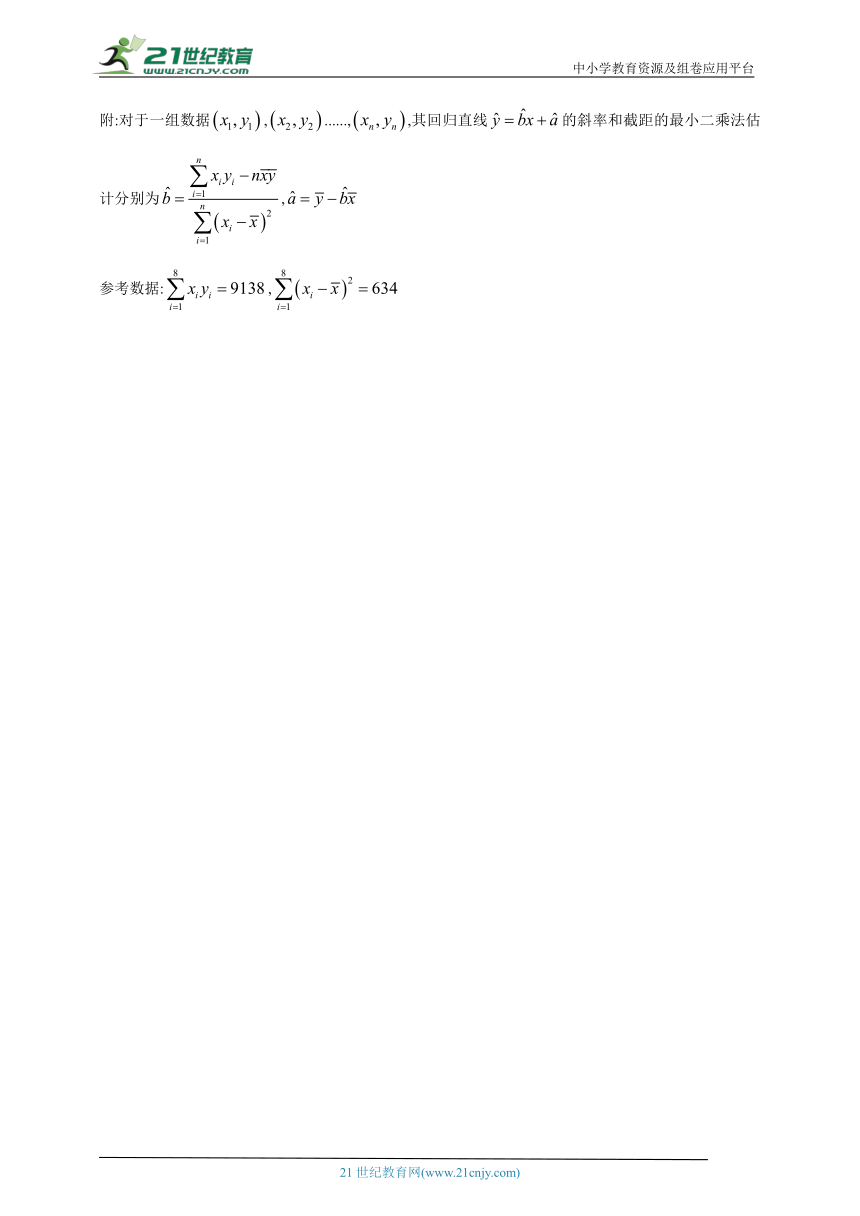
文档简介
中小学教育资源及组卷应用平台
9.1 线性回归分解题思路(同步测试)-高中数学苏教版(2019)选择性必修2
一、选择题
1.调查某校高三学生的身高x和体重y得到如图所示散点图,其中身高x和体重y相关系数,则下列说法正确的是( )
A.学生身高和体重没有相关性
B.学生身高和体重呈正相关
C.学生身高和体重呈负相关
D.若从样本中抽取一部分,则这部分的相关系数一定是0.8255
2.已知变量x和y的统计数据如下表:
x 1 2 3 4 5
y 0.9 1.3 1.8 2.4 3.1
若x,y线性相关,经验回归方程为,据此可以预测当时,( )
A.5.75 B.7.5 C.7.55 D.8
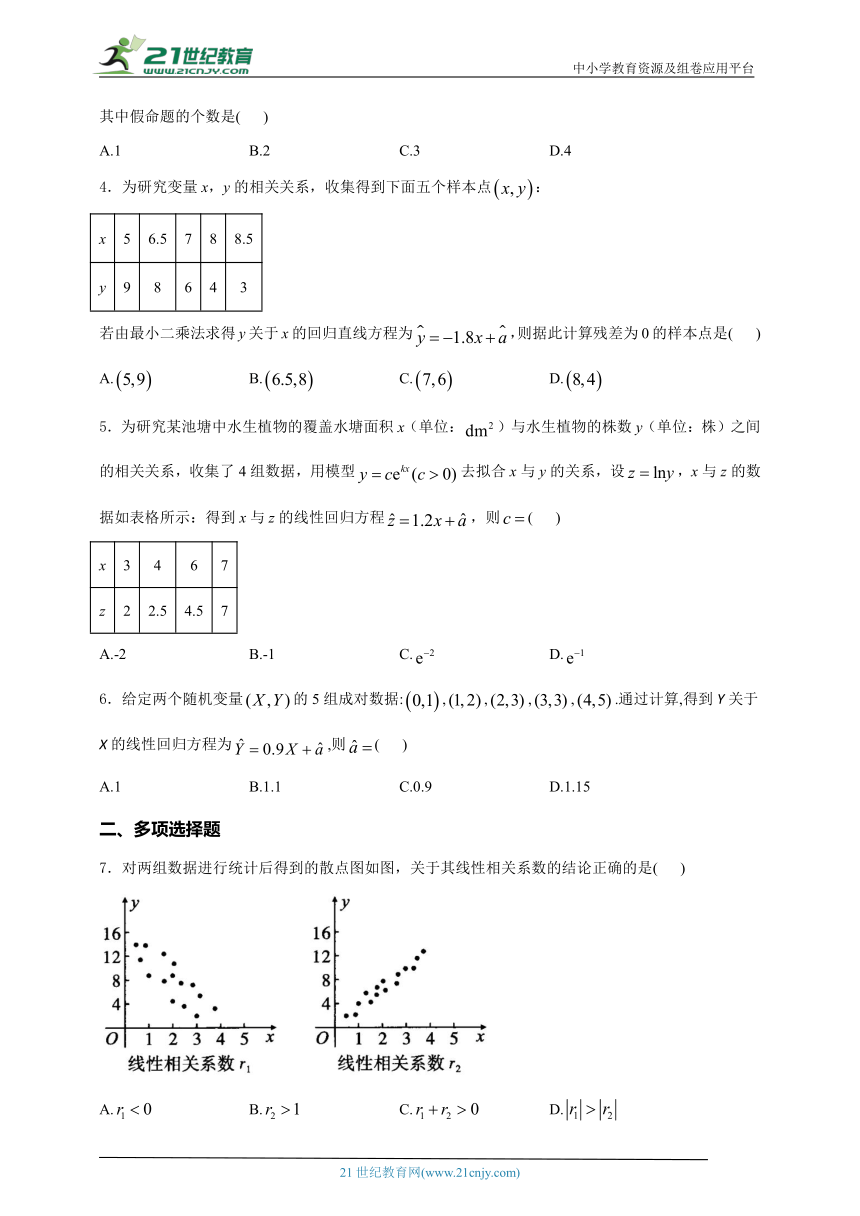
3.下列命题中:
①线性回归方程必过点;
②在回归方程中,当变量x增加一个单位时,y平均增加5个单位;
③在回归解题思路中,相关指数为0.80的模型比相关指数为0.98的模型拟合的效果要好;
④在回归直线中,变量时,变量y的值一定是.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
4.为研究变量x,y的相关关系,收集得到下面五个样本点:
x 5 6.5 7 8 8.5
y 9 8 6 4 3
若由最小二乘法求得y关于x的回归直线方程为,则据此计算残差为0的样本点是( )
A. B. C. D.
5.为研究某池塘中水生植物的覆盖水塘面积x(单位:)与水生植物的株数y(单位:株)之间的相关关系,收集了4组数据,用模型去拟合x与y的关系,设,x与z的数据如表格所示:得到x与z的线性回归方程,则( )
x 3 4 6 7
z 2 2.5 4.5 7
A.-2 B.-1 C. D.
6.给定两个随机变量的5组成对数据:,,,,.通过计算,得到Y关于X的线性回归方程为,则( )
A.1 B.1.1 C.0.9 D.1.15
二、多项选择题
7.对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
A. B. C. D.
8.使用统计手段科学预测传染病可以保障人民群众的生命健康.下表和散点图为某段时间内全球某传染病感染病例在第一次监测到之后数量随时间的变化,以时间为自变量x(单位为天),以监测到的病例总数为因变量y,选择以下两个回归模型拟合y随x的变化:回归模型一:;回归模型二:,通过计算得出,;,,则下列说法正确的是( )
x 1 5 7 12 16 20
y 2 9 12 29 63 101
A.使用回归模型一拟合的决定系数大于使用回归模型二的决定系数
B.通过模型二得出的经验回归方程的预报效果好于通过模型一得出的经验回归方程
C.在首例病例出现后45天,该传染病感染人数很有可能在200人左右
D.在首例病例出现后45天,该传染病的感染人数很有可能超过10000人
三、填空题
9.已知变量x与y的取值如下表:
x 2 3 5 6
y 7 12
若y对x呈现线性相关关系,则y与x的线性回归直线必经过的定点为________.
10.对具有线性相关关系的变量x,y有一组观测数据,,,其经验回归方程,则在样本点处的残差为________.
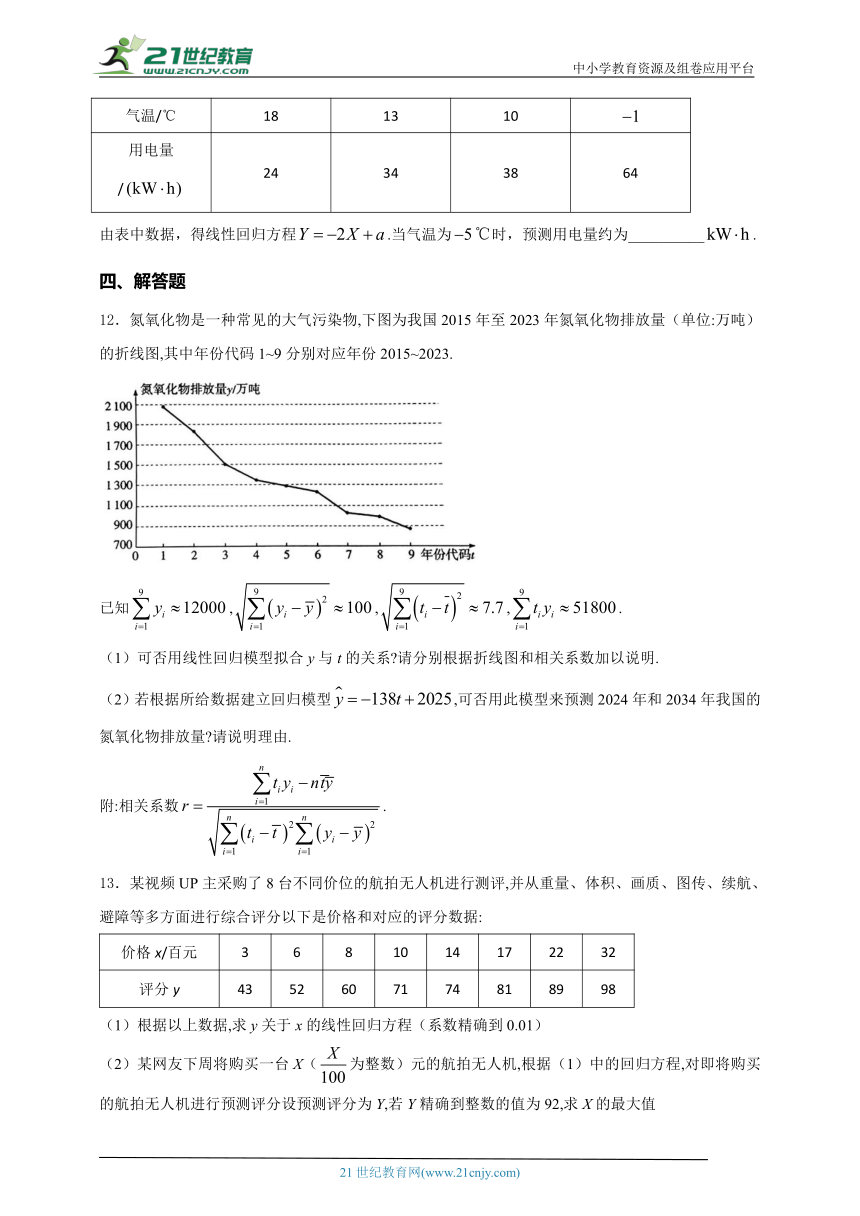
11.某单位为了制定节能减排的目标,先调查了用电量与气温之间的关系,随机统计了某4天的用电量与当天气温,并制成了对照表:
气温/℃ 18 13 10
用电量/ 24 34 38 64
由表中数据,得线性回归方程.当气温为时,预测用电量约为__________.
四、解答题
12.氮氧化物是一种常见的大气污染物,下图为我国2015年至2023年氮氧化物排放量(单位:万吨)的折线图,其中年份代码1~9分别对应年份2015~2023.
已知,,,.
(1)可否用线性回归模型拟合y与t的关系 请分别根据折线图和相关系数加以说明.
(2)若根据所给数据建立回归模型,可否用此模型来预测2024年和2034年我国的氮氧化物排放量 请说明理由.
附:相关系数.
13.某视频UP主采购了8台不同价位的航拍无人机进行测评,并从重量、体积、画质、图传、续航、避障等多方面进行综合评分以下是价格和对应的评分数据:
价格x/百元 3 6 8 10 14 17 22 32
评分y 43 52 60 71 74 81 89 98
(1)根据以上数据,求y关于x的线性回归方程(系数精确到0.01)
(2)某网友下周将购买一台X(为整数)元的航拍无人机,根据(1)中的回归方程,对即将购买的航拍无人机进行预测评分设预测评分为Y,若Y精确到整数的值为92,求X的最大值
附:对于一组数据,......,,其回归直线的斜率和截距的最小二乘法估计分别为,
参考数据:,
参考答案
1.答案:B
解析:由散点图可知,散点的分布集中在一条直线附近,所以学生身高和体重具有相关性,A不正确;又身高x和体重y的相关系数为,相关系数,
所以学生身高和体重呈正相关,B正确,C不正确;从样本中抽取一部分,相关性可能变强,也可能变弱,所以这部分的相关系数不一定是0.8255,D不正确.故选:B.
2.答案:A
解析:,,
所以,即,
令,解得.
故选:A.
3.答案:C
解析:对于①,线性回归方程必过点,满足回归直线的性质,所以①正确;
对于②,在回归方程中,当变量x增加一个单位时,y平均减少5个单位,不是增加5个单位,所以②不正确;
对于③,在回归解题思路中,相关指数为的模型比相关指数为的模型拟合的效果要好,该判断恰好相反,所以③不正确;
对于④,在回归直线中,变量时,变量y的值一定是,不是一定为,而是可能是,也可能在附近,所以④不正确.
故选:C.
4.答案:C
解析:由题意可知,,,
所以回归方程的样本中心点为,
因此有,
所以,
在收集的5个样本点中,一点在上,故计算残差为0的样本点是.
故选:C.
5.答案:C
解析:由已知可得,,,
所以,有,解得,
所以,,
由,得,
所以,,则.
故选:C.
6.答案:A
解析:因为,,
所以,解得,
故选:A
7.答案:AC
解析:由线性相关系数的图像可知,Y与X呈负相关,则,故A正确.由线性相关系数的图像可知,Y与X呈正相关,则,故B错误.线性相关系数的点较线性相关系数的点密集,,,故C正确,D错误.选AC.
8.答案:BD
解析:根据散点图可知模型二的拟合效果更好,拟合效果越好决定系数越大,
所以使用回归模型一拟合的决定系数小于使用回归模型二的决定系数,
所以A错误,B正确;
因为模型二的的拟合效果好,预报更准确,根据已知:,
,,所以,将代入经验回归方程,
有,所以C错误,D正确.
故选:BD
9.答案:
解析:因为,,
所以线性回归方程必过定点.
故答案为:
10.答案:0.5/
解析:将,代入,得,解得,
所以,
故当时,,
所以残差.
故答案为:0.5.
11.答案:70
解析:由表格中的数据,得,,即样本中心点坐标为.又点在回归直线上,,解得,.当时,,即气温为时,预测用电量约为.
12.答案:(1)见解析
(2)见解析
解析:(1)从折线图看,各点落在一条直线附近,因而可以用线性回归模型拟合y与t的关系
由题意知,
相关系数.
,因而可以用线性回归模型拟合y与t的关系.
(2)可以预测2024年的氮氧化物排放量,但不可以预测2034年的氮氧化物排放量.
理由如下:
①2024年与所给数据的年份较接近,因而可以认为短期内氮氧化物排放量将延续该趋势,故可以用此模型进行预测;
②2034年与所给数据的年份相距过远,而影响氮氧化物排放量的因素有很多,这些因素在短期内可能保持不变,但从长期看很有可能会变化,因而用此模型预测可能是不准确的.
13.答案:(1)
(2)2500
解析:(1),
,
,
,
所以y关于x的线性回归方程为
(2),得
因为为整数,所以的最大值为25,即X的最大值为2500
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
9.1 线性回归分解题思路(同步测试)-高中数学苏教版(2019)选择性必修2
一、选择题
1.调查某校高三学生的身高x和体重y得到如图所示散点图,其中身高x和体重y相关系数,则下列说法正确的是( )
A.学生身高和体重没有相关性
B.学生身高和体重呈正相关
C.学生身高和体重呈负相关
D.若从样本中抽取一部分,则这部分的相关系数一定是0.8255
2.已知变量x和y的统计数据如下表:
x 1 2 3 4 5
y 0.9 1.3 1.8 2.4 3.1
若x,y线性相关,经验回归方程为,据此可以预测当时,( )
A.5.75 B.7.5 C.7.55 D.8
3.下列命题中:
①线性回归方程必过点;
②在回归方程中,当变量x增加一个单位时,y平均增加5个单位;
③在回归解题思路中,相关指数为0.80的模型比相关指数为0.98的模型拟合的效果要好;
④在回归直线中,变量时,变量y的值一定是.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
4.为研究变量x,y的相关关系,收集得到下面五个样本点:
x 5 6.5 7 8 8.5
y 9 8 6 4 3
若由最小二乘法求得y关于x的回归直线方程为,则据此计算残差为0的样本点是( )
A. B. C. D.
5.为研究某池塘中水生植物的覆盖水塘面积x(单位:)与水生植物的株数y(单位:株)之间的相关关系,收集了4组数据,用模型去拟合x与y的关系,设,x与z的数据如表格所示:得到x与z的线性回归方程,则( )
x 3 4 6 7
z 2 2.5 4.5 7
A.-2 B.-1 C. D.
6.给定两个随机变量的5组成对数据:,,,,.通过计算,得到Y关于X的线性回归方程为,则( )
A.1 B.1.1 C.0.9 D.1.15
二、多项选择题
7.对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
A. B. C. D.
8.使用统计手段科学预测传染病可以保障人民群众的生命健康.下表和散点图为某段时间内全球某传染病感染病例在第一次监测到之后数量随时间的变化,以时间为自变量x(单位为天),以监测到的病例总数为因变量y,选择以下两个回归模型拟合y随x的变化:回归模型一:;回归模型二:,通过计算得出,;,,则下列说法正确的是( )
x 1 5 7 12 16 20
y 2 9 12 29 63 101
A.使用回归模型一拟合的决定系数大于使用回归模型二的决定系数
B.通过模型二得出的经验回归方程的预报效果好于通过模型一得出的经验回归方程
C.在首例病例出现后45天,该传染病感染人数很有可能在200人左右
D.在首例病例出现后45天,该传染病的感染人数很有可能超过10000人
三、填空题
9.已知变量x与y的取值如下表:
x 2 3 5 6
y 7 12
若y对x呈现线性相关关系,则y与x的线性回归直线必经过的定点为________.
10.对具有线性相关关系的变量x,y有一组观测数据,,,其经验回归方程,则在样本点处的残差为________.
11.某单位为了制定节能减排的目标,先调查了用电量与气温之间的关系,随机统计了某4天的用电量与当天气温,并制成了对照表:
气温/℃ 18 13 10
用电量/ 24 34 38 64
由表中数据,得线性回归方程.当气温为时,预测用电量约为__________.
四、解答题
12.氮氧化物是一种常见的大气污染物,下图为我国2015年至2023年氮氧化物排放量(单位:万吨)的折线图,其中年份代码1~9分别对应年份2015~2023.
已知,,,.
(1)可否用线性回归模型拟合y与t的关系 请分别根据折线图和相关系数加以说明.
(2)若根据所给数据建立回归模型,可否用此模型来预测2024年和2034年我国的氮氧化物排放量 请说明理由.
附:相关系数.
13.某视频UP主采购了8台不同价位的航拍无人机进行测评,并从重量、体积、画质、图传、续航、避障等多方面进行综合评分以下是价格和对应的评分数据:
价格x/百元 3 6 8 10 14 17 22 32
评分y 43 52 60 71 74 81 89 98
(1)根据以上数据,求y关于x的线性回归方程(系数精确到0.01)
(2)某网友下周将购买一台X(为整数)元的航拍无人机,根据(1)中的回归方程,对即将购买的航拍无人机进行预测评分设预测评分为Y,若Y精确到整数的值为92,求X的最大值
附:对于一组数据,......,,其回归直线的斜率和截距的最小二乘法估计分别为,
参考数据:,
参考答案
1.答案:B
解析:由散点图可知,散点的分布集中在一条直线附近,所以学生身高和体重具有相关性,A不正确;又身高x和体重y的相关系数为,相关系数,
所以学生身高和体重呈正相关,B正确,C不正确;从样本中抽取一部分,相关性可能变强,也可能变弱,所以这部分的相关系数不一定是0.8255,D不正确.故选:B.
2.答案:A
解析:,,
所以,即,
令,解得.
故选:A.
3.答案:C
解析:对于①,线性回归方程必过点,满足回归直线的性质,所以①正确;
对于②,在回归方程中,当变量x增加一个单位时,y平均减少5个单位,不是增加5个单位,所以②不正确;
对于③,在回归解题思路中,相关指数为的模型比相关指数为的模型拟合的效果要好,该判断恰好相反,所以③不正确;
对于④,在回归直线中,变量时,变量y的值一定是,不是一定为,而是可能是,也可能在附近,所以④不正确.
故选:C.
4.答案:C
解析:由题意可知,,,
所以回归方程的样本中心点为,
因此有,
所以,
在收集的5个样本点中,一点在上,故计算残差为0的样本点是.
故选:C.
5.答案:C
解析:由已知可得,,,
所以,有,解得,
所以,,
由,得,
所以,,则.
故选:C.
6.答案:A
解析:因为,,
所以,解得,
故选:A
7.答案:AC
解析:由线性相关系数的图像可知,Y与X呈负相关,则,故A正确.由线性相关系数的图像可知,Y与X呈正相关,则,故B错误.线性相关系数的点较线性相关系数的点密集,,,故C正确,D错误.选AC.
8.答案:BD
解析:根据散点图可知模型二的拟合效果更好,拟合效果越好决定系数越大,
所以使用回归模型一拟合的决定系数小于使用回归模型二的决定系数,
所以A错误,B正确;
因为模型二的的拟合效果好,预报更准确,根据已知:,
,,所以,将代入经验回归方程,
有,所以C错误,D正确.
故选:BD
9.答案:
解析:因为,,
所以线性回归方程必过定点.
故答案为:
10.答案:0.5/
解析:将,代入,得,解得,
所以,
故当时,,
所以残差.
故答案为:0.5.
11.答案:70
解析:由表格中的数据,得,,即样本中心点坐标为.又点在回归直线上,,解得,.当时,,即气温为时,预测用电量约为.
12.答案:(1)见解析
(2)见解析
解析:(1)从折线图看,各点落在一条直线附近,因而可以用线性回归模型拟合y与t的关系
由题意知,
相关系数.
,因而可以用线性回归模型拟合y与t的关系.
(2)可以预测2024年的氮氧化物排放量,但不可以预测2034年的氮氧化物排放量.
理由如下:
①2024年与所给数据的年份较接近,因而可以认为短期内氮氧化物排放量将延续该趋势,故可以用此模型进行预测;
②2034年与所给数据的年份相距过远,而影响氮氧化物排放量的因素有很多,这些因素在短期内可能保持不变,但从长期看很有可能会变化,因而用此模型预测可能是不准确的.
13.答案:(1)
(2)2500
解析:(1),
,
,
,
所以y关于x的线性回归方程为
(2),得
因为为整数,所以的最大值为25,即X的最大值为2500
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
