沪科版数学八年级上册 期末综合测试卷(五)(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 期末综合测试卷(五)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 14:28:19 | ||
图片预览



文档简介
期末综合测试卷(五)
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,是轴对称图形的是( )
2.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性.这样做的道理是( )
A.两点之间的所有连线中线段最短
B.三角形具有稳定性
C.经过两点有一条直线,并且只有一条直线拉杆
D.在连接直线外一点与直线上各点的线段中,垂线段最短
3.下列命题是假命题的是( )
A.三角形三边垂直平分线的交点到三角形的三个顶点的距离相等
B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16
C.将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限
D.若关于x的一元一次不等式组无解,则m的取值范围是m≤1
4.已知点A(x1,a),B(x1+1,b)都在函数y=-2x+3的图象上, 下列对于a, b的关系判断正确的是( )
A. a+b=-2 B. a+b=2 C. a-b=-2 D. a-b=2
5. 如图,点P是∠AOB的角平分线OC上一点,PN⊥OB 于点N,点M 是线段ON上一点.已知OM=3,ON=5,点D为OA上一点若满足PD=PM,则OD的长度为( )
A.3 B.5 C.5和7 D.3和7
6.如图, 已知点O为△ABC的两条角平分线的交点, 过点O作OD⊥BC, 垂足为D, 且OD=4.若△ABC的面积是34,则△ABC的周长为 ( )
A.8.5 B.15 C.17 D.34
7.已知一次函数y= mx+4与一次函数y=2x+n关于x轴对称,则m,n分别为 ( )
A. m=-2,n=4 B. m= -2,n= -4 C. m=2,n=4 D. m=2,n= -4
8.如图,已知△ABC≌△A'B'C,∠A=40° ,∠CBA=60° ,A'C交边AB 于点 P(点P不与A,B重合).BO,CO分别平分∠CBA,∠BCP,若m°<∠BOCA.20 B.40 C.60 D.100
如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB =40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为
( )
A.4 B.3 C.2 D.1
10.如图1,甲、乙两人沿湟水河滨水绿道同向而行,甲步行的速度为100米/分,乙骑公共自行车的速度为v米/分,起初甲在乙前a米处,两人同时出发,当乙追上甲时,两人停止前行.设x分钟后甲、乙两人相距y米,y与x的函数关系如图2所示.有以下结论:①图1中a表示为1 000;②图1中EF 表示为1000-200x;③乙的速度为200米/分;④若两人在相距a米处同时相向而行. 分钟后相遇.其中正确的结论( )
A.①② B.③④ C.①②③ D.①③④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,CD是△ABC的角平分线,AE⊥CD于E,BC=6,AC=4,△ABC的面积是9,则△AEC 的面积是 .
12. 如图,在△ABC和△DBC中,∠A=40° ,AB=AC=2,∠BDC=140° ,BD=CD.以点D为顶点作 ∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为 .
13. 在平面直角坐标系中,已知点A(0,-1),B(-1,-2),点P在x轴上运动,当点P到A,B两点距离之差的绝对值最大时,点P 的坐标是 .
14.如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x,y轴于点A,B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点 C,则直线 BC的函数表达式是 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD,求证:CF=DE.
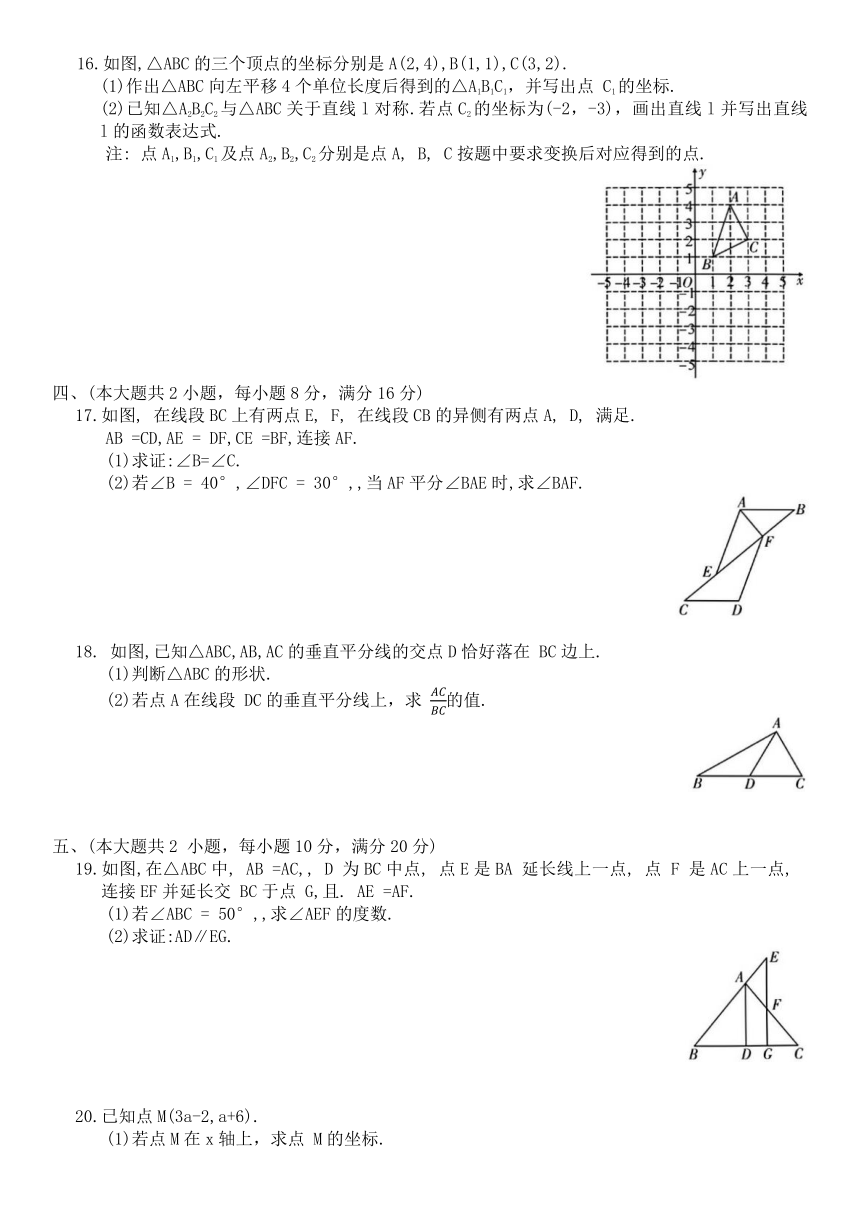
16.如图,△ABC的三个顶点的坐标分别是A(2,4),B(1,1),C(3,2).
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点 C1的坐标.
(2)已知△A2B2C2与△ABC关于直线l对称.若点C2的坐标为(-2,-3),画出直线l并写出直线l的函数表达式.
注: 点A1,B1,C1及点A2,B2,C2分别是点A, B, C按题中要求变换后对应得到的点.
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 在线段BC上有两点E, F, 在线段CB的异侧有两点A, D, 满足.
AB =CD,AE = DF,CE =BF,连接AF.
(1)求证:∠B=∠C.
(2)若∠B = 40°,∠DFC = 30°,,当AF平分∠BAE时,求∠BAF.
18. 如图,已知△ABC,AB,AC的垂直平分线的交点D恰好落在 BC边上.
(1)判断△ABC的形状.
(2)若点A在线段 DC的垂直平分线上,求 的值.
五、(本大题共2 小题,每小题10分,满分20分)
19.如图,在△ABC中, AB =AC,, D 为BC中点, 点E是BA 延长线上一点, 点 F 是AC上一点, 连接EF并延长交 BC于点 G,且. AE =AF.
(1)若∠ABC = 50°,,求∠AEF的度数.
(2)求证:AD∥EG.
20.已知点M(3a-2,a+6).
(1)若点M在x轴上,求点 M的坐标.
(2)已知点N(2,5),且直线MN∥x轴,求点M 的坐标.
(3)点M到x轴、y轴的距离相等,求点M的坐标.
六、(本题满分12分)
21.在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A,B两种客车,A型客车的载客量为45人/辆,每辆租金为400元; B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数表达式.
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
七、(本题满分12分)
22.(1)如图1,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线, 试判断AB, AD, DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证 得到AB =FC, 从而把AB, AD, DC转化在一个三角形中即可判断.
AB,AD,DC之间的等量关系为 .
(2)问题探究: 如图2, 在四边形ABCD中, AB||CD,AF 与DC 的延长线交于点 F,点 E 是 BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
八、(本题满分14分)
23. 在平面直角坐标系中,已知点A(0,a),B(b,c),且
(1)直接写出a =,
(2)如图1,点P在x轴上,PG||AB,∠GPO,∠BAO的补角的角平分线交于点F, 求出∠F的度数.
(3)如图2,作射线BO,过A作. 已知 是平面内一点,问当a满足什么条件时,∠CAQ --∠OBQ =∠AQB总是成立的
期末综合测试卷(五)
1. D2. B3. B4. D5. D6. C7. B8. B9. B
15.证明:∵AE =BF,∴AE +EF = BF +EF,即AF = BE,
∵AC||BD,∴∠CAF =∠DBE
在△ACF和△BDE中,
∴△ACF △BDE(SAS),∴CF =DE.
16.解:(1)如图, △A1B1C1即可为所作,
(2)如图,直线为所作,
∴直线l的函数表达式为: y = x.
17.(1)证明:∵
CE=BF,∴CE+EF=BF+EF,∴BE=CF,
在△ABE和△DCF中,
∴△ABE≌△DCF(SSS),∴∠B=∠C.
(2)解:由(1)得△ABE≌△DCF,
∴∠AEB=∠DFC=30°,
∵AF平分.
18.解:(1)△ABC为直角三角形.
∵AB,AC的垂直平分线的交点落在BC边上,
∴AD=BD,AD=CD,
又∵ ,
即)=180°,
∴∠BAD+∠DAC=90°,即
∴△ABC为直角三角形.
(2)∵点A在线段DC的垂直平分线上,∴AD=AC,又∵DA=DC,∴AD=DC=AC,
∴△ADC为等边三角形,
又·.
19.解:(1)∵AB=AC,∴∠B=∠C=50°,
(2)证明:∵AB=AC,点 D 是BC的中点,
∵AE=AF,∴∠AEF=∠AFE,
∵∠BAD+∠CAD=∠BAC=∠AEF+∠AFE,
∴∠AEF=∠BAD,∴AD||EG.
20.解:(1)∵点M在x轴上,∴a+6=0,∴a=-6.
3a-2=-18-2 =-20,
∴ 点M的坐标是(-20,0).
(2)∵直线MN∥x轴,∴a+6=5,
解得a=-1,∴3a-2=3x(-1)-2=-5,
∴点 M的坐标为(-5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a-2=a+6,或3a-2+a+6=0
解得a=4,或a=-1,
当a=4时,3a-2=a+6=10,
当a=-1时,3a-2=-5,a+6=5,
∴点M的坐标为(10,10)或(-5,5).
21.解:(1)设租用A型客车x辆,
则租用B型客车(5-x)辆,
由题意得
(2)由题意:45x+30(5-x)≥205,解得
∵x是整数,且0≤x≤5,∴x=4或5.
∵y=120x+1400,120>0,
∴y随x的增大而增大.
当x=4时,y最小=120×4+1400=1880(元).
此时5-x=1.
此时租车方案为租用A型客车4辆,租用B型客车1 辆.
22.解:(1)∵AE是∠BAD的平分线,∴∠DAE=∠BAE.
∵AB||CD,∴∠F=∠BAE,∴∠DAF=∠F,∴AD=DF.
∵点E是BC的中点,∴CE=BE,又
∵∠F=∠BAE,∠AEB=∠FEC,
∴AB=CF,∴△AEB≌△FEC(AAS),∴AB=CF,∴DF=DC+CF=DC+AB,
又∵AD=DF,∴AD=AB+DC.故答案为:AD=AB+DC.
(2)AB=AF+CF.
证明如下:如图2,延长AE 交 DF 的延长线于点G,
∵E是BC的中点,∴CE=BE,
∵AB∥DC,∴∠BAE=∠G,
又∵∠AEB =∠GEC,
∴△AEB≌△GEC(AAS),∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG.
∵∠BAG=∠G,∴∠FAG=∠G,
∴FA=FG,∵CG=CF+FG,∴AB=AF+CF.
23.解:
∴a-4=0,b-3=0,c-2=0,∴a=4,b=3,c=2,故答案为:4;3;2.
(2)设PF与AB的交点为点 E,如图1,
∵PG||AB,∴∠BAO=∠PGO,
∵∠POG=90°,∴∠PGO+∠OPG=90°,
∴∠BAO+∠OPG=90°,
设∠BAO=x°,则∠OPG=(90-x)°,
∵∠GPO,∠BAO的补角的角平分线交于点 F.
(3)当Q点不在OB与直线y=-1的交点D的左边时,
∠CAQ-∠OBQ=∠AQB 总是成立的.过Q作QK∥AC∥OB,如图2.
则有∠CAQ=∠AQK,∠OBQ=∠BQK,
∵∠AQK-∠BQK=∠AQB,
∴∠CAQ-∠OBQ=∠AQB,设OB的表达式为y= kx(k≠0).
∵B(3,2),∴3k=2,∴k=2/3,
∴直线OB的表达式为:
令y=-1,得
解得
∵Q(a,-1)不在D的左边,∴a
即当 时,∠CAQ-∠OBQ =∠AQB 总是成立的.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,是轴对称图形的是( )
2.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性.这样做的道理是( )
A.两点之间的所有连线中线段最短
B.三角形具有稳定性
C.经过两点有一条直线,并且只有一条直线拉杆
D.在连接直线外一点与直线上各点的线段中,垂线段最短
3.下列命题是假命题的是( )
A.三角形三边垂直平分线的交点到三角形的三个顶点的距离相等
B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16
C.将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限
D.若关于x的一元一次不等式组无解,则m的取值范围是m≤1
4.已知点A(x1,a),B(x1+1,b)都在函数y=-2x+3的图象上, 下列对于a, b的关系判断正确的是( )
A. a+b=-2 B. a+b=2 C. a-b=-2 D. a-b=2
5. 如图,点P是∠AOB的角平分线OC上一点,PN⊥OB 于点N,点M 是线段ON上一点.已知OM=3,ON=5,点D为OA上一点若满足PD=PM,则OD的长度为( )
A.3 B.5 C.5和7 D.3和7
6.如图, 已知点O为△ABC的两条角平分线的交点, 过点O作OD⊥BC, 垂足为D, 且OD=4.若△ABC的面积是34,则△ABC的周长为 ( )
A.8.5 B.15 C.17 D.34
7.已知一次函数y= mx+4与一次函数y=2x+n关于x轴对称,则m,n分别为 ( )
A. m=-2,n=4 B. m= -2,n= -4 C. m=2,n=4 D. m=2,n= -4
8.如图,已知△ABC≌△A'B'C,∠A=40° ,∠CBA=60° ,A'C交边AB 于点 P(点P不与A,B重合).BO,CO分别平分∠CBA,∠BCP,若m°<∠BOC
如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB =40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为
( )
A.4 B.3 C.2 D.1
10.如图1,甲、乙两人沿湟水河滨水绿道同向而行,甲步行的速度为100米/分,乙骑公共自行车的速度为v米/分,起初甲在乙前a米处,两人同时出发,当乙追上甲时,两人停止前行.设x分钟后甲、乙两人相距y米,y与x的函数关系如图2所示.有以下结论:①图1中a表示为1 000;②图1中EF 表示为1000-200x;③乙的速度为200米/分;④若两人在相距a米处同时相向而行. 分钟后相遇.其中正确的结论( )
A.①② B.③④ C.①②③ D.①③④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,CD是△ABC的角平分线,AE⊥CD于E,BC=6,AC=4,△ABC的面积是9,则△AEC 的面积是 .
12. 如图,在△ABC和△DBC中,∠A=40° ,AB=AC=2,∠BDC=140° ,BD=CD.以点D为顶点作 ∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为 .
13. 在平面直角坐标系中,已知点A(0,-1),B(-1,-2),点P在x轴上运动,当点P到A,B两点距离之差的绝对值最大时,点P 的坐标是 .
14.如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x,y轴于点A,B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点 C,则直线 BC的函数表达式是 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD,求证:CF=DE.
16.如图,△ABC的三个顶点的坐标分别是A(2,4),B(1,1),C(3,2).
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点 C1的坐标.
(2)已知△A2B2C2与△ABC关于直线l对称.若点C2的坐标为(-2,-3),画出直线l并写出直线l的函数表达式.
注: 点A1,B1,C1及点A2,B2,C2分别是点A, B, C按题中要求变换后对应得到的点.
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 在线段BC上有两点E, F, 在线段CB的异侧有两点A, D, 满足.
AB =CD,AE = DF,CE =BF,连接AF.
(1)求证:∠B=∠C.
(2)若∠B = 40°,∠DFC = 30°,,当AF平分∠BAE时,求∠BAF.
18. 如图,已知△ABC,AB,AC的垂直平分线的交点D恰好落在 BC边上.
(1)判断△ABC的形状.
(2)若点A在线段 DC的垂直平分线上,求 的值.
五、(本大题共2 小题,每小题10分,满分20分)
19.如图,在△ABC中, AB =AC,, D 为BC中点, 点E是BA 延长线上一点, 点 F 是AC上一点, 连接EF并延长交 BC于点 G,且. AE =AF.
(1)若∠ABC = 50°,,求∠AEF的度数.
(2)求证:AD∥EG.
20.已知点M(3a-2,a+6).
(1)若点M在x轴上,求点 M的坐标.
(2)已知点N(2,5),且直线MN∥x轴,求点M 的坐标.
(3)点M到x轴、y轴的距离相等,求点M的坐标.
六、(本题满分12分)
21.在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A,B两种客车,A型客车的载客量为45人/辆,每辆租金为400元; B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数表达式.
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
七、(本题满分12分)
22.(1)如图1,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线, 试判断AB, AD, DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证 得到AB =FC, 从而把AB, AD, DC转化在一个三角形中即可判断.
AB,AD,DC之间的等量关系为 .
(2)问题探究: 如图2, 在四边形ABCD中, AB||CD,AF 与DC 的延长线交于点 F,点 E 是 BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
八、(本题满分14分)
23. 在平面直角坐标系中,已知点A(0,a),B(b,c),且
(1)直接写出a =,
(2)如图1,点P在x轴上,PG||AB,∠GPO,∠BAO的补角的角平分线交于点F, 求出∠F的度数.
(3)如图2,作射线BO,过A作. 已知 是平面内一点,问当a满足什么条件时,∠CAQ --∠OBQ =∠AQB总是成立的
期末综合测试卷(五)
1. D2. B3. B4. D5. D6. C7. B8. B9. B
15.证明:∵AE =BF,∴AE +EF = BF +EF,即AF = BE,
∵AC||BD,∴∠CAF =∠DBE
在△ACF和△BDE中,
∴△ACF △BDE(SAS),∴CF =DE.
16.解:(1)如图, △A1B1C1即可为所作,
(2)如图,直线为所作,
∴直线l的函数表达式为: y = x.
17.(1)证明:∵
CE=BF,∴CE+EF=BF+EF,∴BE=CF,
在△ABE和△DCF中,
∴△ABE≌△DCF(SSS),∴∠B=∠C.
(2)解:由(1)得△ABE≌△DCF,
∴∠AEB=∠DFC=30°,
∵AF平分.
18.解:(1)△ABC为直角三角形.
∵AB,AC的垂直平分线的交点落在BC边上,
∴AD=BD,AD=CD,
又∵ ,
即)=180°,
∴∠BAD+∠DAC=90°,即
∴△ABC为直角三角形.
(2)∵点A在线段DC的垂直平分线上,∴AD=AC,又∵DA=DC,∴AD=DC=AC,
∴△ADC为等边三角形,
又·.
19.解:(1)∵AB=AC,∴∠B=∠C=50°,
(2)证明:∵AB=AC,点 D 是BC的中点,
∵AE=AF,∴∠AEF=∠AFE,
∵∠BAD+∠CAD=∠BAC=∠AEF+∠AFE,
∴∠AEF=∠BAD,∴AD||EG.
20.解:(1)∵点M在x轴上,∴a+6=0,∴a=-6.
3a-2=-18-2 =-20,
∴ 点M的坐标是(-20,0).
(2)∵直线MN∥x轴,∴a+6=5,
解得a=-1,∴3a-2=3x(-1)-2=-5,
∴点 M的坐标为(-5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a-2=a+6,或3a-2+a+6=0
解得a=4,或a=-1,
当a=4时,3a-2=a+6=10,
当a=-1时,3a-2=-5,a+6=5,
∴点M的坐标为(10,10)或(-5,5).
21.解:(1)设租用A型客车x辆,
则租用B型客车(5-x)辆,
由题意得
(2)由题意:45x+30(5-x)≥205,解得
∵x是整数,且0≤x≤5,∴x=4或5.
∵y=120x+1400,120>0,
∴y随x的增大而增大.
当x=4时,y最小=120×4+1400=1880(元).
此时5-x=1.
此时租车方案为租用A型客车4辆,租用B型客车1 辆.
22.解:(1)∵AE是∠BAD的平分线,∴∠DAE=∠BAE.
∵AB||CD,∴∠F=∠BAE,∴∠DAF=∠F,∴AD=DF.
∵点E是BC的中点,∴CE=BE,又
∵∠F=∠BAE,∠AEB=∠FEC,
∴AB=CF,∴△AEB≌△FEC(AAS),∴AB=CF,∴DF=DC+CF=DC+AB,
又∵AD=DF,∴AD=AB+DC.故答案为:AD=AB+DC.
(2)AB=AF+CF.
证明如下:如图2,延长AE 交 DF 的延长线于点G,
∵E是BC的中点,∴CE=BE,
∵AB∥DC,∴∠BAE=∠G,
又∵∠AEB =∠GEC,
∴△AEB≌△GEC(AAS),∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG.
∵∠BAG=∠G,∴∠FAG=∠G,
∴FA=FG,∵CG=CF+FG,∴AB=AF+CF.
23.解:
∴a-4=0,b-3=0,c-2=0,∴a=4,b=3,c=2,故答案为:4;3;2.
(2)设PF与AB的交点为点 E,如图1,
∵PG||AB,∴∠BAO=∠PGO,
∵∠POG=90°,∴∠PGO+∠OPG=90°,
∴∠BAO+∠OPG=90°,
设∠BAO=x°,则∠OPG=(90-x)°,
∵∠GPO,∠BAO的补角的角平分线交于点 F.
(3)当Q点不在OB与直线y=-1的交点D的左边时,
∠CAQ-∠OBQ=∠AQB 总是成立的.过Q作QK∥AC∥OB,如图2.
则有∠CAQ=∠AQK,∠OBQ=∠BQK,
∵∠AQK-∠BQK=∠AQB,
∴∠CAQ-∠OBQ=∠AQB,设OB的表达式为y= kx(k≠0).
∵B(3,2),∴3k=2,∴k=2/3,
∴直线OB的表达式为:
令y=-1,得
解得
∵Q(a,-1)不在D的左边,∴a
即当 时,∠CAQ-∠OBQ =∠AQB 总是成立的.
同课章节目录
