北京市师达中学2024~2025学年第一学期初二月考数学试卷(10月份)(pdf版无答案)
文档属性
| 名称 | 北京市师达中学2024~2025学年第一学期初二月考数学试卷(10月份)(pdf版无答案) |  | |
| 格式 | |||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 14:41:03 | ||
图片预览

文档简介
北京市师达中学20242025学年度第“学期第一次大练习
初二数学
2024.10
一、选择题(每小题3分,共30分)
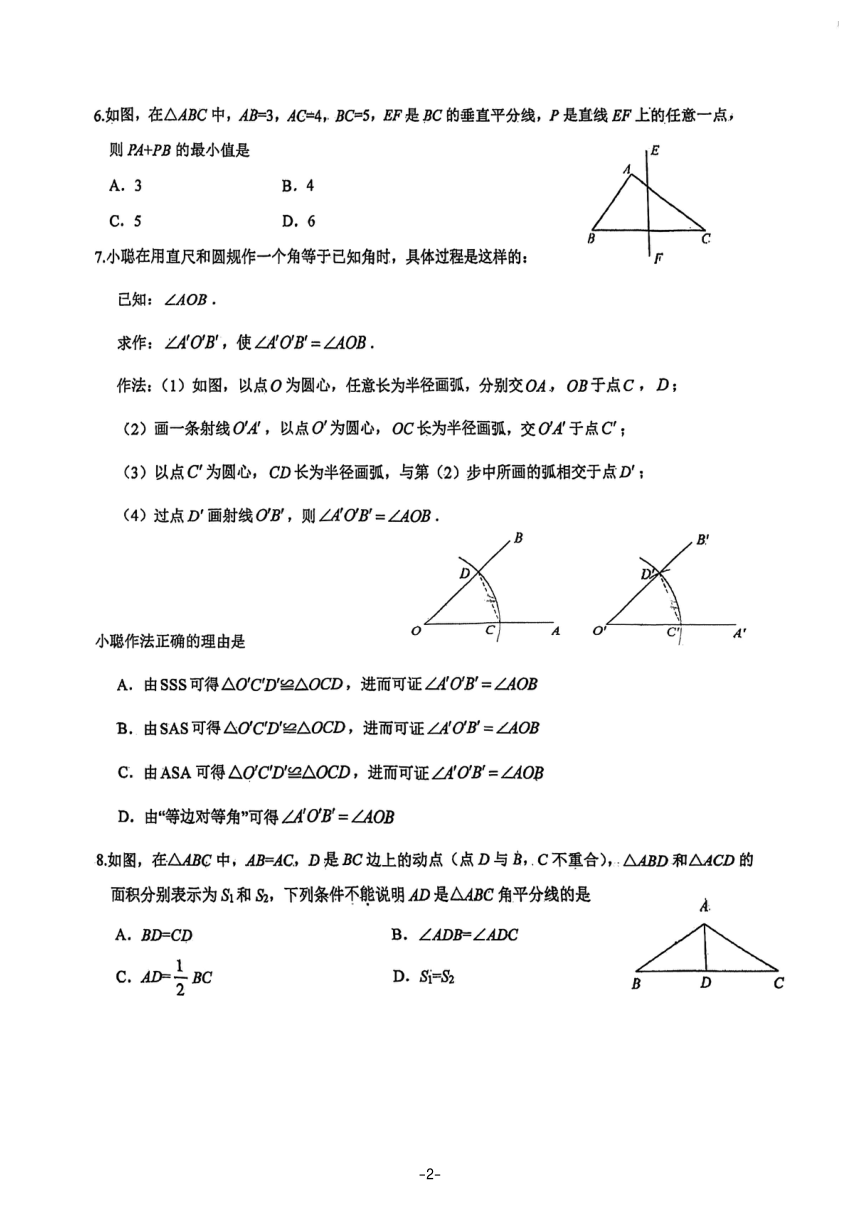
1.斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在
许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是
A.
B
2如图所示,△ABC中4AB边上的高线画法正确的是
A.
C
D
3如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角大小为
A.135°
B.140°
C.144
D.150°
4如图是折叠凳及其侧面示意图.若AC=BC=18cm,则折叠凳的宽AB可能为
A.70cm
B,50cm
C.40
D.25 cm
5.右图中的两个三角形全等,则∠1等于
A.58
B.72
C40°
D.50
-1-
6如图,在△ABC中,AB=3,AC=4,BC-5,EF是BC的垂直平分线,P是直线EF上的任意一点,
则P+PB的最小值是
A.3
B.4
C.5
D.6
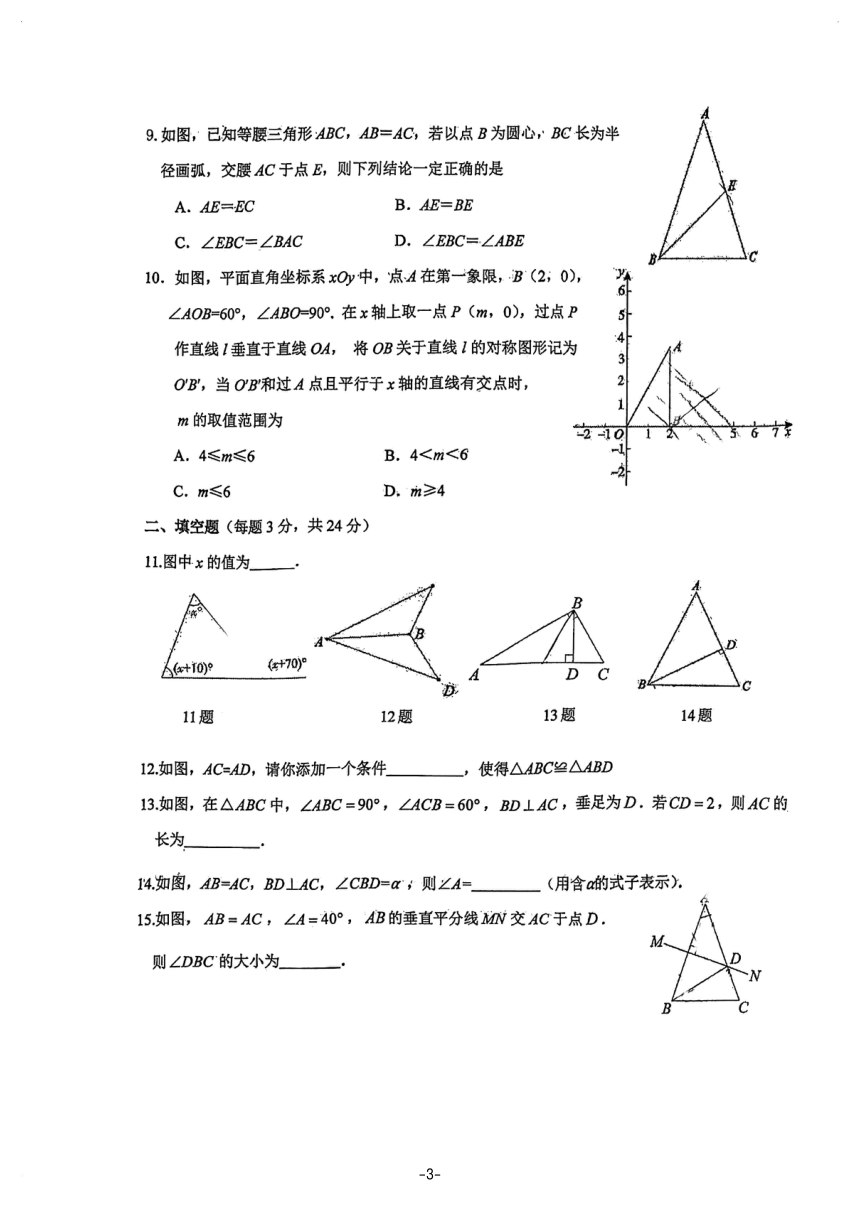
7小聪在用直尺和圆规作一个角等于已知角时,具体过程是这样的:
已知:∠AOB.
求作:∠A'OB,使∠AOB=∠AOB.
作法:(1)如图,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D:
(2)画一条射线OA”,以点O'为圆心,OC长为半径画弧,交04于点C;
(3)以点C为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D':
(4)过点D'画射线OB,则∠A'OB=∠AOB,
B
小聪作法正确的理由是
C
A.由SSS可得△OC'D'≌△OCD,进而可证∠AOB=∠AOB
B.由SAS可得△OCD'2△OCD,进而可证∠A'OB=∠AOB
C.由ASA可得△OC'D'≌△OCD,进而可证∠AOB=∠AOB
D.由“等边对等角”可得∠A'OB=∠AOB
8.如图,在△ABC中,AB=AC,D是BC边上的动点(点D与B,.C不重合),:△ABD和△ACD的
面积分别表示为S和S2,下列条件不能说明AD是△ABC角平分线的是
A.BD=CD
B.∠ADB=∠ADC
C.ADBC
D.Si=S2
-2
9如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半
径画弧,交腰AC于点E,则下列结论一定正确的是
A.AE-EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
10.如图,平面直角坐标系x0y中,点A在第一象限,B(2;0),
6
∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P
作直线1垂直于直线OA,将OB关于直线1的对称图形记为
OB,当OB和过A点且平行子x轴的直线有交点时,
m的取值范围为
A.4≤m≤6
B.4C,m≤6
D.m≥4
二、填空题(每题3分,共24分)
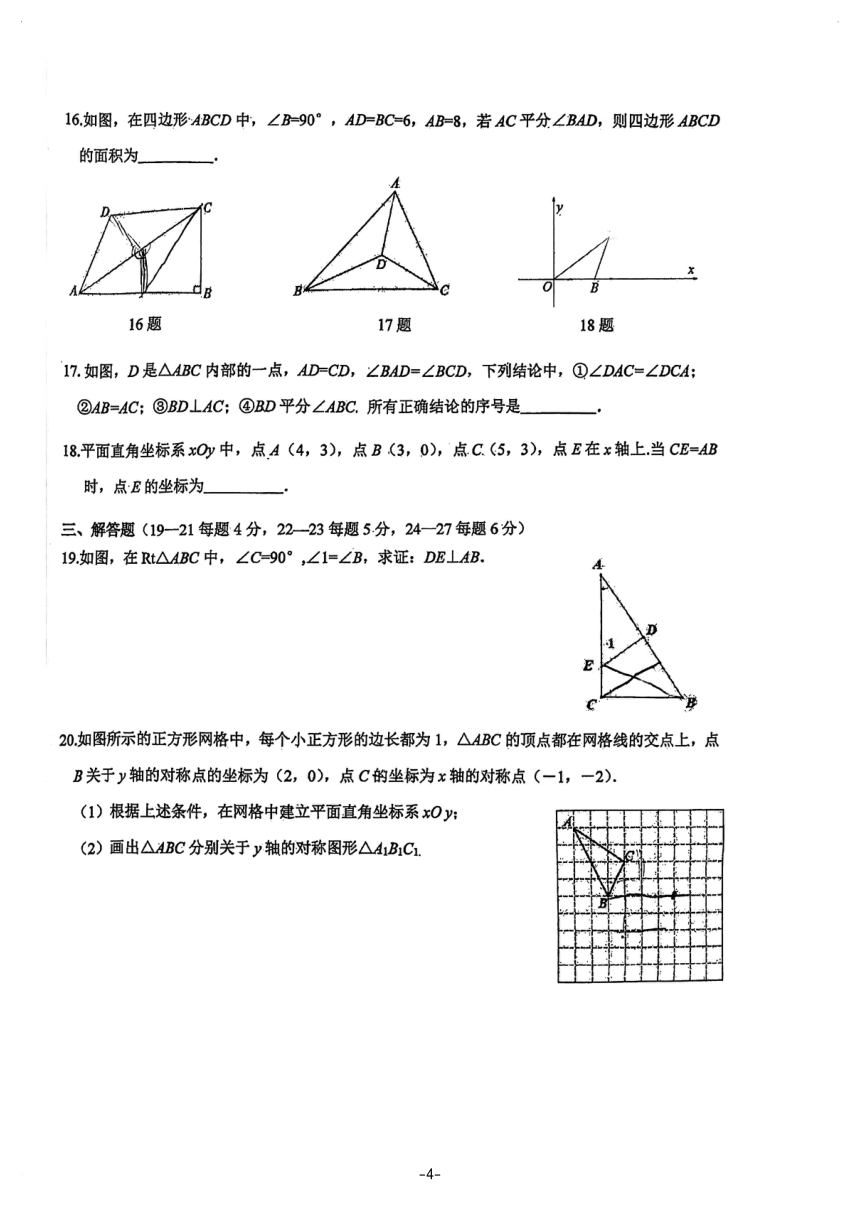
11.图中x的值为
D
a+i09
(+70)°
D
11题
12题
13题
14题
12.如图,AC=AD,请你添加一个条件
使得△ABC≌△ABD
13如图,在△ABC中,∠ABC=90°,∠ACB=60°,BD LAC,垂足为D.若CD=2,则AC的
长为
14如图,AB=AC,BD LAC,∠CBD=a',则∠A=」
(用含a的式子表示上.
15如图,AB=AC,∠A=40°,AB的垂直平分线N交AC于点D.
则∠DBC的大小为
-3-
初二数学
2024.10
一、选择题(每小题3分,共30分)
1.斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在
许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是
A.
B
2如图所示,△ABC中4AB边上的高线画法正确的是
A.
C
D
3如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角大小为
A.135°
B.140°
C.144
D.150°
4如图是折叠凳及其侧面示意图.若AC=BC=18cm,则折叠凳的宽AB可能为
A.70cm
B,50cm
C.40
D.25 cm
5.右图中的两个三角形全等,则∠1等于
A.58
B.72
C40°
D.50
-1-
6如图,在△ABC中,AB=3,AC=4,BC-5,EF是BC的垂直平分线,P是直线EF上的任意一点,
则P+PB的最小值是
A.3
B.4
C.5
D.6
7小聪在用直尺和圆规作一个角等于已知角时,具体过程是这样的:
已知:∠AOB.
求作:∠A'OB,使∠AOB=∠AOB.
作法:(1)如图,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D:
(2)画一条射线OA”,以点O'为圆心,OC长为半径画弧,交04于点C;
(3)以点C为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D':
(4)过点D'画射线OB,则∠A'OB=∠AOB,
B
小聪作法正确的理由是
C
A.由SSS可得△OC'D'≌△OCD,进而可证∠AOB=∠AOB
B.由SAS可得△OCD'2△OCD,进而可证∠A'OB=∠AOB
C.由ASA可得△OC'D'≌△OCD,进而可证∠AOB=∠AOB
D.由“等边对等角”可得∠A'OB=∠AOB
8.如图,在△ABC中,AB=AC,D是BC边上的动点(点D与B,.C不重合),:△ABD和△ACD的
面积分别表示为S和S2,下列条件不能说明AD是△ABC角平分线的是
A.BD=CD
B.∠ADB=∠ADC
C.ADBC
D.Si=S2
-2
9如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半
径画弧,交腰AC于点E,则下列结论一定正确的是
A.AE-EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
10.如图,平面直角坐标系x0y中,点A在第一象限,B(2;0),
6
∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P
作直线1垂直于直线OA,将OB关于直线1的对称图形记为
OB,当OB和过A点且平行子x轴的直线有交点时,
m的取值范围为
A.4≤m≤6
B.4
D.m≥4
二、填空题(每题3分,共24分)
11.图中x的值为
D
a+i09
(+70)°
D
11题
12题
13题
14题
12.如图,AC=AD,请你添加一个条件
使得△ABC≌△ABD
13如图,在△ABC中,∠ABC=90°,∠ACB=60°,BD LAC,垂足为D.若CD=2,则AC的
长为
14如图,AB=AC,BD LAC,∠CBD=a',则∠A=」
(用含a的式子表示上.
15如图,AB=AC,∠A=40°,AB的垂直平分线N交AC于点D.
则∠DBC的大小为
-3-
同课章节目录
