浙江省杭州市拱墅区华东师范大学附属杭州学校2024-2025学年九年级上学期10月月考数学试卷(pdf版,无答案)
文档属性
| 名称 | 浙江省杭州市拱墅区华东师范大学附属杭州学校2024-2025学年九年级上学期10月月考数学试卷(pdf版,无答案) | 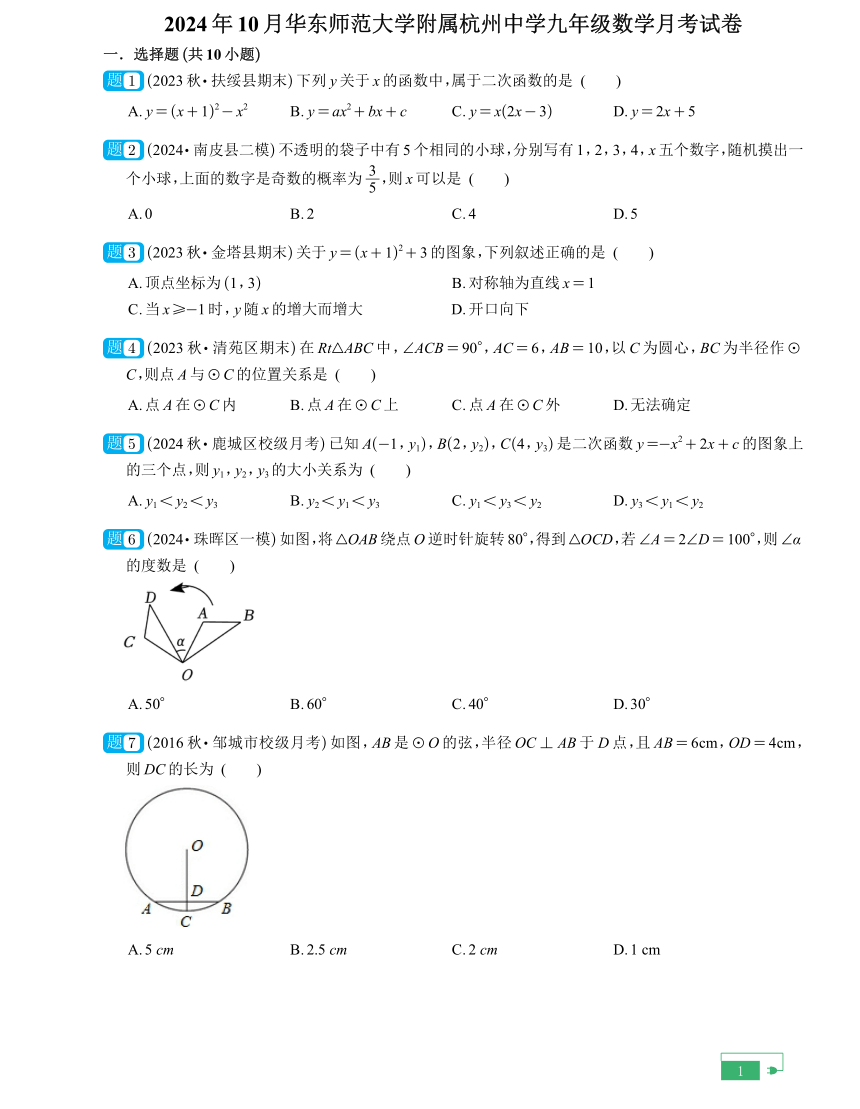 | |
| 格式 | |||
| 文件大小 | 758.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 16:38:18 | ||
图片预览

文档简介
2024年10月华师附九年级月考数学试卷
2024年 10月华东师范大学附属杭州中学九年级数学月考试卷
一.选择题 (共 10小题)
1 (2023秋 扶绥县期末)下列 y关于 x的函数中,属于二次函数的是 ( )
A. y= (x+ 1)2- x2 B. y= ax2+ bx+ c C. y= x(2x- 3) D. y= 2x+ 5
2 (2024 南皮县二模)不透明的袋子中有 5个相同的小球,分别写有 1,2,3,4,x五个数字,随机摸出一
3
个小球,上面的数字是奇数的概率为 5 ,则 x可以是 ( )
A. 0 B. 2 C. 4 D. 5
3 (2023秋 金塔县期末)关于 y= (x+ 1)2+ 3的图象,下列叙述正确的是 ( )
A.顶点坐标为 (1,3) B.对称轴为直线 x= 1
C.当 x≥-1时,y随 x的增大而增大 D.开口向下
4 (2023秋 清苑区期末)在 Rt△ABC中,∠ACB= 90°,AC= 6,AB= 10,以 C为圆心,BC为半径作⊙
C,则点 A与⊙C的位置关系是 ( )
A.点 A在⊙C内 B.点 A在⊙C上 C.点 A在⊙C外 D.无法确定
5 (2024秋 鹿城区校级月考)已知 A(-1,y1),B(2,y2),C(4,y3)是二次函数 y=-x2+ 2x+ c的图象上
的三个点,则 y1,y2,y3的大小关系为 ( )
A. y1< y2< y3 B. y2< y1< y3 C. y1< y3< y2 D. y3< y1< y2
6 (2024 珠晖区一模)如图,将△OAB绕点O逆时针旋转 80°,得到△OCD,若∠A= 2∠D= 100°,则∠α
的度数是 ( )
A. 50° B. 60° C. 40° D. 30°
7 (2016秋 邹城市校级月考)如图,AB是⊙O的弦,半径OC⊥ AB于D点,且 AB= 6cm,OD= 4cm,
则DC的长为 ( )
A. 5 cm B. 2.5 cm C. 2 cm D. 1 cm
1
{#{QQABTSQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
幂 思 课 堂 让数学更简单
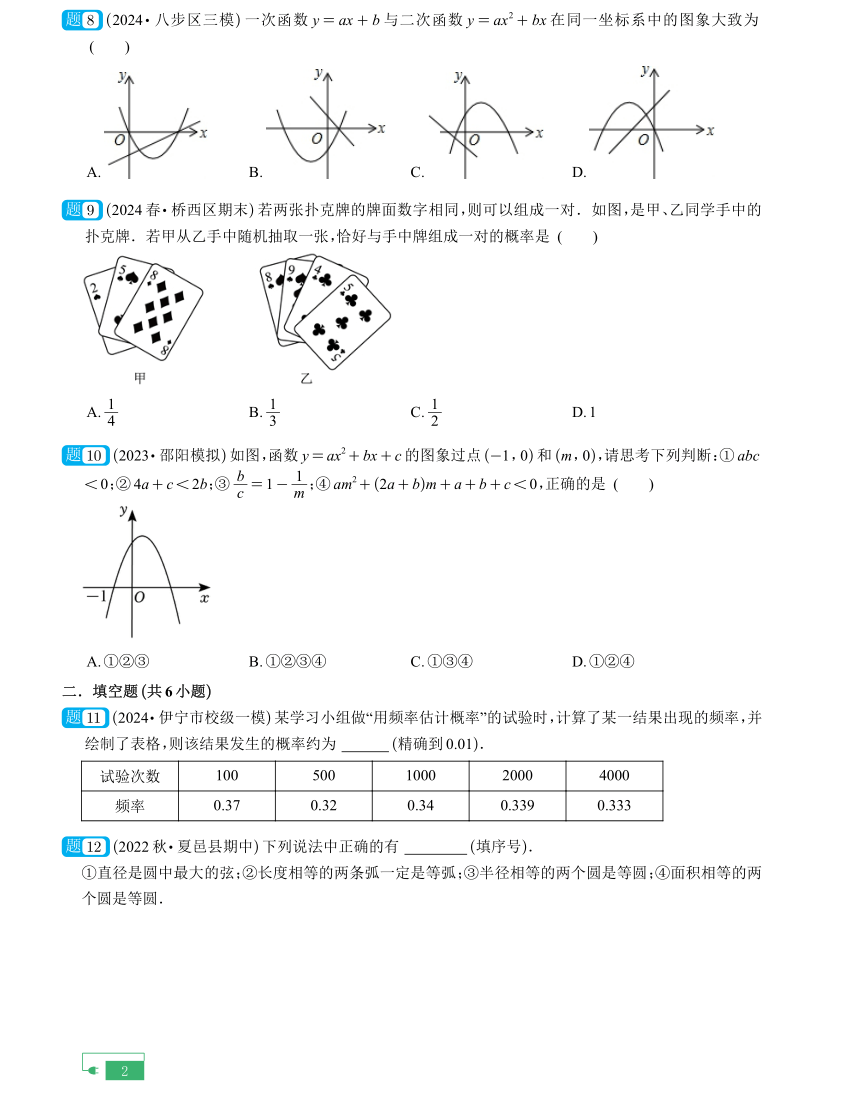
8 (2024 八步区三模)一次函数 y= ax + b与二次函数 y= ax2+ bx在同一坐标系中的图象大致为
( )
A. B. C. D.
9 (2024春 桥西区期末)若两张扑克牌的牌面数字相同,则可以组成一对.如图,是甲、乙同学手中的
扑克牌.若甲从乙手中随机抽取一张,恰好与手中牌组成一对的概率是 ( )
A. 14 B.
1
3 C.
1
2 D. 1
10 (2023 邵阳模拟)如图,函数 y= ax2+ bx+ c的图象过点 (-1,0)和 (m,0),请思考下列判断:① abc
< 0;② 4a+ c< 2b b 1;③ c = 1- m;④ am
2+ (2a+ b)m+ a+ b+ c< 0,正确的是 ( )
A.①②③ B.①②③④ C.①③④ D.①②④
二.填空题 (共 6小题)
11 (2024 伊宁市校级一模)某学习小组做“用频率估计概率”的试验时,计算了某一结果出现的频率,并
绘制了表格,则该结果发生的概率约为 (精确到 0.01).
试验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.34 0.339 0.333
12 (2022秋 夏邑县期中)下列说法中正确的有 (填序号).
①直径是圆中最大的弦;②长度相等的两条弧一定是等弧;③半径相等的两个圆是等圆;④面积相等的两
个圆是等圆.
2
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年10月华师附九年级月考数学试卷
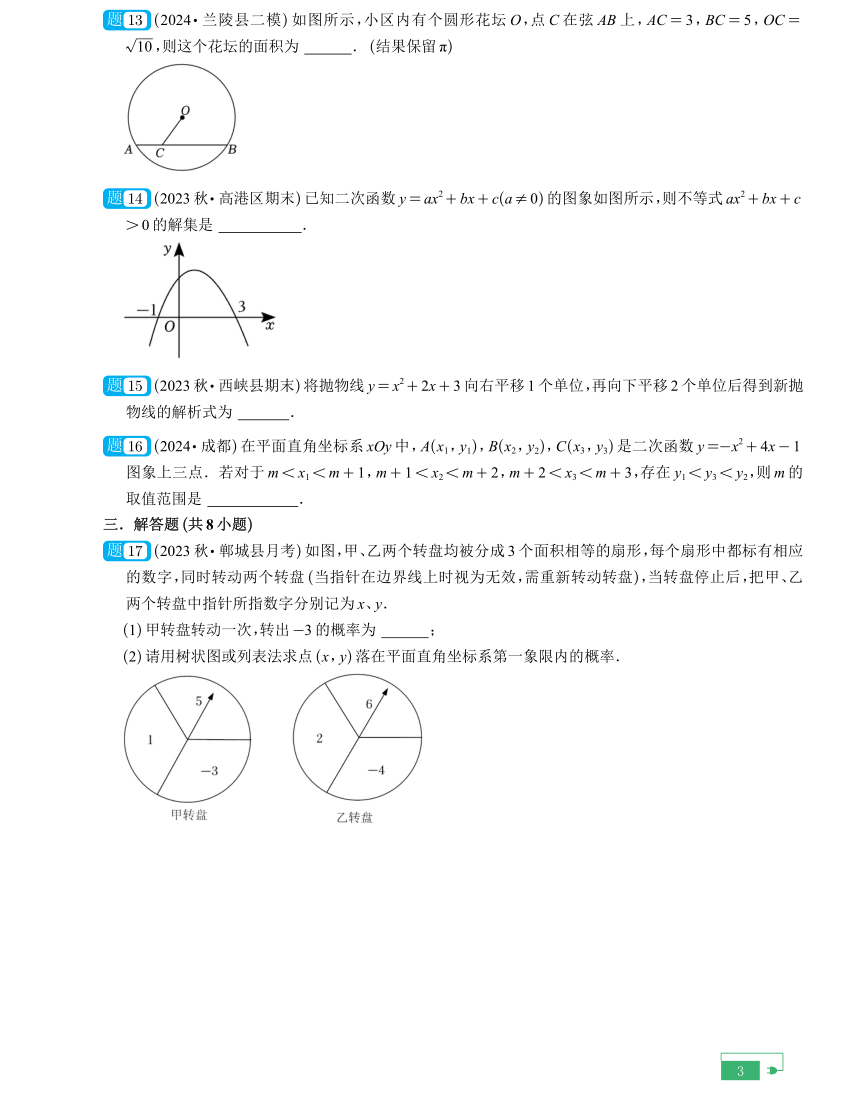
13 (2024 兰陵县二模)如图所示,小区内有个圆形花坛 O,点 C在弦 AB上,AC= 3,BC= 5,OC=
10,则这个花坛的面积为 . (结果保留 π)
14 (2023秋 高港区期末)已知二次函数 y= ax2+ bx+ c(a≠ 0)的图象如图所示,则不等式 ax2+ bx+ c
> 0的解集是 .
15 (2023秋 西峡县期末)将抛物线 y= x2+ 2x+ 3向右平移 1个单位,再向下平移 2个单位后得到新抛
物线的解析式为 .
16 (2024 成都)在平面直角坐标系 xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是二次函数 y=-x2+ 4x- 1
图象上三点.若对于m< x1取值范围是 .
三.解答题 (共 8小题)
17 (2023秋 郸城县月考)如图,甲、乙两个转盘均被分成 3个面积相等的扇形,每个扇形中都标有相应
的数字,同时转动两个转盘 (当指针在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙
两个转盘中指针所指数字分别记为 x、y.
(1)甲转盘转动一次,转出-3的概率为 ;
(2)请用树状图或列表法求点 (x,y)落在平面直角坐标系第一象限内的概率.
3
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
幂 思 课 堂 让数学更简单
18 (1)求二次函数 y= 2x2+ 8x- 3这个函数图象的顶点坐标;
(2)求二次函数 y=-x2- 4x+ 5的最大值.
19 按要求作图,
(1)作△ABC的外接圆;(尺规作图,保留作图痕迹,不写作法).
(2)O是△ABC外的一点,以O为旋转中心,将△ABC按顺时针方向旋转 90度,作出经旋转后的图形,(尺
规和量角器作图,保留作图痕迹,不写作法)
C C
A A O
B B
20 (2023秋 崇川区校级月考)如图,在以O为圆心的两个同心圆中,大圆的弦 AB交小圆于C、D两点,
若 AB= 16cm,CD= 6cm.
(1)求 AC的长;
(2)若大圆半径为 10cm,求小圆的半径.
4
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年10月华师附九年级月考数学试卷
21 (2023秋 历城区期末)如图,学校课外兴趣活动小组准备利用长为 8m的墙 AB和一段长为 26m的篱
笆围建一个矩形苗圃园.如果矩形苗圃园的一边由墙 AB和一节篱笆 BF构成,另三边由篱笆 ACDF围
成,设平行于墙一边CD长为 x m.
(1)当苗圃园的面积为 60m2时,求 x的值.
(2)当 x为何值时,所围苗圃园的面积最大?最大面积是多少?
22 (2023 贵阳模拟)已知函数 y= x2+ bx+ c(b,c为常数)的图象经过点 (0,3),(6,3).
(1)求 b,c的值;
(2)当 0≤ x≤ 4时,求 y的最大值与最小值之差;
(3)当 k- 4≤ x≤ k时,若 y的最大值与最小值之差为 8,求 k的值.
5
{#{QQABTSQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
幂 思 课 堂 让数学更简单
23 (2024 济南模拟)某数学小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中
心考察.
【知识背景】“道路千万条,安全第一条”刹车后还要继续向前行驶一段距离才能停止,这段距离成为刹车
距离.
【探究发现】汽车研发中心设计一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹
车性能进行测试,数学小组收集、整理数据,并绘制函数图象.
发现:开始刹车后行驶的距离 y(单位:m)与刹车后行驶时间 t(单位:s)之间成二次函数关系,函数图象如
图所示.
【问题解决】请根据以上信息,完成下列问题:
(1)求二次函数的解析式 (不要求写出自变量的取值范围);
(2)若在汽车前 60m处,有一测速仪,当汽车刹车过程中,经过多少时间,汽车与测速仪相距 12m;
(3)若汽车司机发现正前方 80m处有一辆抛锚的车停在路面,立刻刹车,问该车在不变道的情况下是否会
撞到抛锚的车?试说明理由.
6
{#{QQABTSQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年10月华师附九年级月考数学试卷
24 (2024 南山区校级模拟)根据以下情境信息,探索完成任务.
公路涵洞改造方案的设计与解决
图 1是某公路涵洞,图 2是其截面示意
图,它由圆心在点O的劣弧 AED和矩
情境 1 形 ABCD构成.测得公路宽 BC= 12m,
涵洞直壁高 AB= 2m,涵洞顶端 E高出
道路 (BC)6m(即 EG= 6m).
现需对公路进行拓宽,改造成双向隔离
车道,并同步拓宽涵洞,中间设置宽为
a(m)的隔离带,两边为机动车道.如图
情境 2
3,改造后的公路宽 BC= 20m,涵洞直壁
高 AB和涵洞顶端 E到 BC的距离保持
不变.
改造方案
如图 4,将涵洞上半部分劣弧 AED改造
方案一
成顶点为 E的抛物线一部分的形式.
如图 5,将涵洞上半部分劣弧 AED改造
方案二
成仍为劣弧的形式
问题解决
以点G为坐标原点,BC所在直线为 x轴建立
任务 1 按方案一改造
平面直角坐标系,求抛物线的函数表达式.
任务 2 按方案二改造 求涵洞上半部分劣弧 AED所在圆的半径.
要使高 5.5m,宽 2.3m的货运车能通过此公路
任务 3 隔离带最大宽度 a的确定 涵洞,分别求出两种改造方案下 a的最大值
( 2 ≈ 1.41, 57 ≈ 7.55,结果精确到 0.1m).
7
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年 10月华东师范大学附属杭州中学九年级数学月考试卷
一.选择题 (共 10小题)
1 (2023秋 扶绥县期末)下列 y关于 x的函数中,属于二次函数的是 ( )
A. y= (x+ 1)2- x2 B. y= ax2+ bx+ c C. y= x(2x- 3) D. y= 2x+ 5
2 (2024 南皮县二模)不透明的袋子中有 5个相同的小球,分别写有 1,2,3,4,x五个数字,随机摸出一
3
个小球,上面的数字是奇数的概率为 5 ,则 x可以是 ( )
A. 0 B. 2 C. 4 D. 5
3 (2023秋 金塔县期末)关于 y= (x+ 1)2+ 3的图象,下列叙述正确的是 ( )
A.顶点坐标为 (1,3) B.对称轴为直线 x= 1
C.当 x≥-1时,y随 x的增大而增大 D.开口向下
4 (2023秋 清苑区期末)在 Rt△ABC中,∠ACB= 90°,AC= 6,AB= 10,以 C为圆心,BC为半径作⊙
C,则点 A与⊙C的位置关系是 ( )
A.点 A在⊙C内 B.点 A在⊙C上 C.点 A在⊙C外 D.无法确定
5 (2024秋 鹿城区校级月考)已知 A(-1,y1),B(2,y2),C(4,y3)是二次函数 y=-x2+ 2x+ c的图象上
的三个点,则 y1,y2,y3的大小关系为 ( )
A. y1< y2< y3 B. y2< y1< y3 C. y1< y3< y2 D. y3< y1< y2
6 (2024 珠晖区一模)如图,将△OAB绕点O逆时针旋转 80°,得到△OCD,若∠A= 2∠D= 100°,则∠α
的度数是 ( )
A. 50° B. 60° C. 40° D. 30°
7 (2016秋 邹城市校级月考)如图,AB是⊙O的弦,半径OC⊥ AB于D点,且 AB= 6cm,OD= 4cm,
则DC的长为 ( )
A. 5 cm B. 2.5 cm C. 2 cm D. 1 cm
1
{#{QQABTSQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
幂 思 课 堂 让数学更简单
8 (2024 八步区三模)一次函数 y= ax + b与二次函数 y= ax2+ bx在同一坐标系中的图象大致为
( )
A. B. C. D.
9 (2024春 桥西区期末)若两张扑克牌的牌面数字相同,则可以组成一对.如图,是甲、乙同学手中的
扑克牌.若甲从乙手中随机抽取一张,恰好与手中牌组成一对的概率是 ( )
A. 14 B.
1
3 C.
1
2 D. 1
10 (2023 邵阳模拟)如图,函数 y= ax2+ bx+ c的图象过点 (-1,0)和 (m,0),请思考下列判断:① abc
< 0;② 4a+ c< 2b b 1;③ c = 1- m;④ am
2+ (2a+ b)m+ a+ b+ c< 0,正确的是 ( )
A.①②③ B.①②③④ C.①③④ D.①②④
二.填空题 (共 6小题)
11 (2024 伊宁市校级一模)某学习小组做“用频率估计概率”的试验时,计算了某一结果出现的频率,并
绘制了表格,则该结果发生的概率约为 (精确到 0.01).
试验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.34 0.339 0.333
12 (2022秋 夏邑县期中)下列说法中正确的有 (填序号).
①直径是圆中最大的弦;②长度相等的两条弧一定是等弧;③半径相等的两个圆是等圆;④面积相等的两
个圆是等圆.
2
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年10月华师附九年级月考数学试卷
13 (2024 兰陵县二模)如图所示,小区内有个圆形花坛 O,点 C在弦 AB上,AC= 3,BC= 5,OC=
10,则这个花坛的面积为 . (结果保留 π)
14 (2023秋 高港区期末)已知二次函数 y= ax2+ bx+ c(a≠ 0)的图象如图所示,则不等式 ax2+ bx+ c
> 0的解集是 .
15 (2023秋 西峡县期末)将抛物线 y= x2+ 2x+ 3向右平移 1个单位,再向下平移 2个单位后得到新抛
物线的解析式为 .
16 (2024 成都)在平面直角坐标系 xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是二次函数 y=-x2+ 4x- 1
图象上三点.若对于m< x1
三.解答题 (共 8小题)
17 (2023秋 郸城县月考)如图,甲、乙两个转盘均被分成 3个面积相等的扇形,每个扇形中都标有相应
的数字,同时转动两个转盘 (当指针在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙
两个转盘中指针所指数字分别记为 x、y.
(1)甲转盘转动一次,转出-3的概率为 ;
(2)请用树状图或列表法求点 (x,y)落在平面直角坐标系第一象限内的概率.
3
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
幂 思 课 堂 让数学更简单
18 (1)求二次函数 y= 2x2+ 8x- 3这个函数图象的顶点坐标;
(2)求二次函数 y=-x2- 4x+ 5的最大值.
19 按要求作图,
(1)作△ABC的外接圆;(尺规作图,保留作图痕迹,不写作法).
(2)O是△ABC外的一点,以O为旋转中心,将△ABC按顺时针方向旋转 90度,作出经旋转后的图形,(尺
规和量角器作图,保留作图痕迹,不写作法)
C C
A A O
B B
20 (2023秋 崇川区校级月考)如图,在以O为圆心的两个同心圆中,大圆的弦 AB交小圆于C、D两点,
若 AB= 16cm,CD= 6cm.
(1)求 AC的长;
(2)若大圆半径为 10cm,求小圆的半径.
4
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年10月华师附九年级月考数学试卷
21 (2023秋 历城区期末)如图,学校课外兴趣活动小组准备利用长为 8m的墙 AB和一段长为 26m的篱
笆围建一个矩形苗圃园.如果矩形苗圃园的一边由墙 AB和一节篱笆 BF构成,另三边由篱笆 ACDF围
成,设平行于墙一边CD长为 x m.
(1)当苗圃园的面积为 60m2时,求 x的值.
(2)当 x为何值时,所围苗圃园的面积最大?最大面积是多少?
22 (2023 贵阳模拟)已知函数 y= x2+ bx+ c(b,c为常数)的图象经过点 (0,3),(6,3).
(1)求 b,c的值;
(2)当 0≤ x≤ 4时,求 y的最大值与最小值之差;
(3)当 k- 4≤ x≤ k时,若 y的最大值与最小值之差为 8,求 k的值.
5
{#{QQABTSQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
幂 思 课 堂 让数学更简单
23 (2024 济南模拟)某数学小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中
心考察.
【知识背景】“道路千万条,安全第一条”刹车后还要继续向前行驶一段距离才能停止,这段距离成为刹车
距离.
【探究发现】汽车研发中心设计一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹
车性能进行测试,数学小组收集、整理数据,并绘制函数图象.
发现:开始刹车后行驶的距离 y(单位:m)与刹车后行驶时间 t(单位:s)之间成二次函数关系,函数图象如
图所示.
【问题解决】请根据以上信息,完成下列问题:
(1)求二次函数的解析式 (不要求写出自变量的取值范围);
(2)若在汽车前 60m处,有一测速仪,当汽车刹车过程中,经过多少时间,汽车与测速仪相距 12m;
(3)若汽车司机发现正前方 80m处有一辆抛锚的车停在路面,立刻刹车,问该车在不变道的情况下是否会
撞到抛锚的车?试说明理由.
6
{#{QQABTSQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
2024年10月华师附九年级月考数学试卷
24 (2024 南山区校级模拟)根据以下情境信息,探索完成任务.
公路涵洞改造方案的设计与解决
图 1是某公路涵洞,图 2是其截面示意
图,它由圆心在点O的劣弧 AED和矩
情境 1 形 ABCD构成.测得公路宽 BC= 12m,
涵洞直壁高 AB= 2m,涵洞顶端 E高出
道路 (BC)6m(即 EG= 6m).
现需对公路进行拓宽,改造成双向隔离
车道,并同步拓宽涵洞,中间设置宽为
a(m)的隔离带,两边为机动车道.如图
情境 2
3,改造后的公路宽 BC= 20m,涵洞直壁
高 AB和涵洞顶端 E到 BC的距离保持
不变.
改造方案
如图 4,将涵洞上半部分劣弧 AED改造
方案一
成顶点为 E的抛物线一部分的形式.
如图 5,将涵洞上半部分劣弧 AED改造
方案二
成仍为劣弧的形式
问题解决
以点G为坐标原点,BC所在直线为 x轴建立
任务 1 按方案一改造
平面直角坐标系,求抛物线的函数表达式.
任务 2 按方案二改造 求涵洞上半部分劣弧 AED所在圆的半径.
要使高 5.5m,宽 2.3m的货运车能通过此公路
任务 3 隔离带最大宽度 a的确定 涵洞,分别求出两种改造方案下 a的最大值
( 2 ≈ 1.41, 57 ≈ 7.55,结果精确到 0.1m).
7
{#{QQABSTQSAsxggqgQAgAIJaIACAQ4hKCQ0w1l4I CUEuGQQkkJAIhGJAcgAMQhgRGCBNAOAAMQsAKACAJFiAAFFAKBAC=A}#=}}#}
同课章节目录
