山东省济南市市中区泉海学校2024-2025学年八年级上学期第一次月考数学试题(pdf版,无答案)
文档属性
| 名称 | 山东省济南市市中区泉海学校2024-2025学年八年级上学期第一次月考数学试题(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 533.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 16:50:53 | ||
图片预览

文档简介
初二数学月考试题
一、选择题(共 10 小题,每小题 4 分,共 40 分)
1.下列选项中,y不是 x函数的是( )
A. B. C. D.
2.下列说法正确的是( )
A.16的算术平方根是±4 B.任何数都有两个平方根
C.因为 3的平方是 9,所以 9的平方根是 3 D.﹣1是 1的平方根
3.下列运算正确的是( )
A. B. C. D.
4.若代数式 有意义,则 x的取值范围是( )
A. B. C. D.
5.平面直角坐标系中,点 P(﹣2,3)关于 x轴对称,得到的点的坐标为( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(3,﹣2)
6. 的整数部分为 m,小数部分为 n,则 m﹣n的值为( )
A. B. C. D.
7.下列变量之间的关系,一个变量是另一个变量的正比例函数关系的是( )
A.圆的面积 S随半径 r的变化而变化
B.用 10m长的绳子围成一个矩形,其中一边长 y随它邻边 x的变化而变化
C.正方形的周长 C 随边长 a 的变化而变化
D.汽车油箱中有汽油 50L,行驶过程中邮箱中的油量 Q 随行驶路程 s的变化而变化
8.若函数 y=(k﹣1)x+(k﹣2)的图象经过第一、三、四象限,则 k的取值范围是( )
A.k>1 B.k>2 C.1<k<2 D.k<1
9.如图所示的“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的,如果小正
方形的面积为 6,大正方形的面积为 14,直角三角形中较短直角边的长为 a,较长直角边
的长为 b,那么 ab的值为( )
A.4 B.6 C. D.
10.数轴上表示 ,π的点分别为 A,B,点 A是 BC的中点,则点 C所表示的数是( )
A. B. C. D.
{#{QQABKLQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
二、填空题(共 6 小题,每小题 4 分,共 24 分)
11.(﹣2)2的平方根是 , 的算术平方根是 , 的立方根是 .
12.已知点 A(﹣3,2m﹣4)在 x轴上,点 B(n+3,4)在 y轴上,则 m+n= .
13.已知点 M(2,3),直线 MN∥x轴,且 MN=3,则点 N的坐标是 .
14.点 A(1,y1)、B(2,y2)在一次函数 y=3x+1的图象上,则 y1 y2(用“<”、“=”或“>”填空).
15.已知函数 是关于 x的一次函数,则 m的值是 .
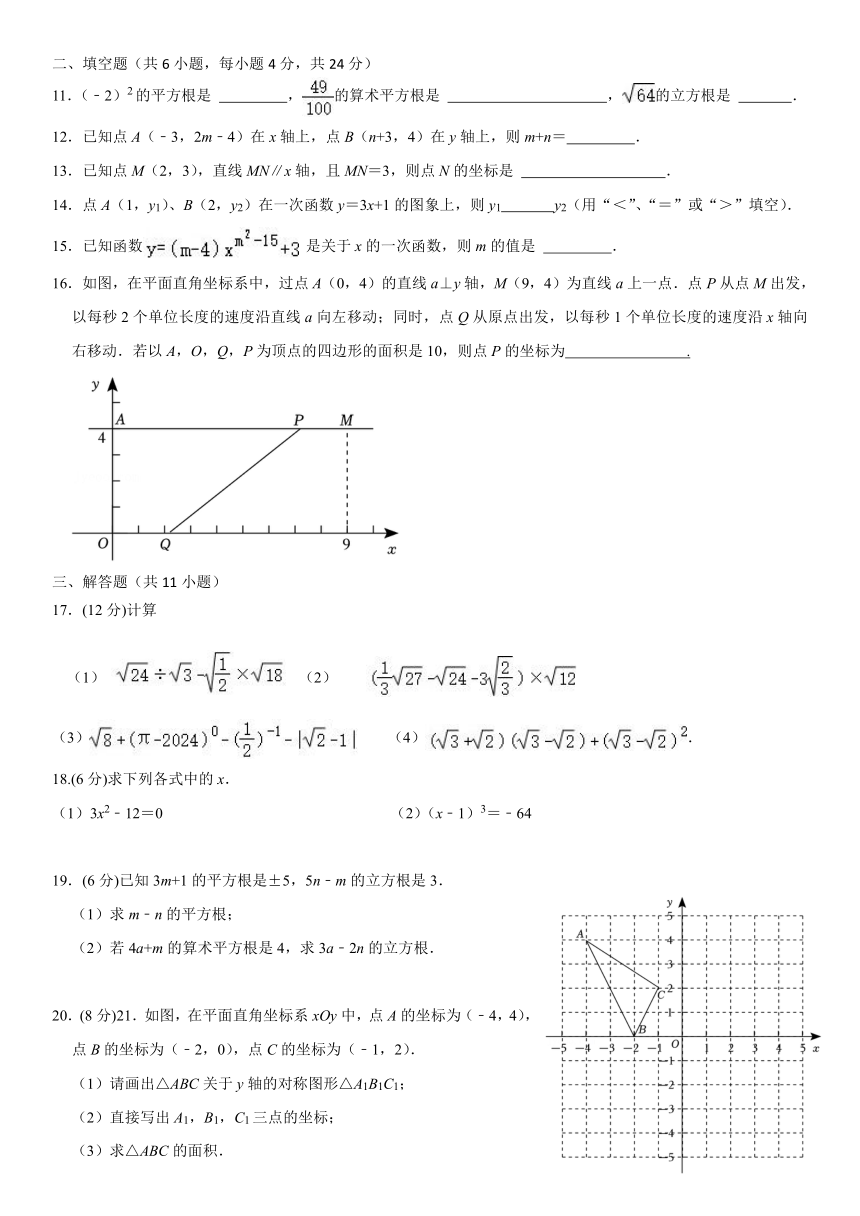
16.如图,在平面直角坐标系中,过点 A(0,4)的直线 a⊥y轴,M(9,4)为直线 a上一点.点 P从点 M出发,
以每秒 2个单位长度的速度沿直线 a向左移动;同时,点 Q从原点出发,以每秒 1个单位长度的速度沿 x轴向
右移动.若以 A,O,Q,P为顶点的四边形的面积是 10,则点 P的坐标为 .
三、解答题(共 11 小题)
17.(12分)计算
(1) (2)
(3) (4) .
18.(6分)求下列各式中的 x.
(1)3x2﹣12=0 (2)(x﹣1)3=﹣64
19.(6分)已知 3m+1的平方根是±5,5n﹣m的立方根是 3.
(1)求 m﹣n的平方根;
(2)若 4a+m的算术平方根是 4,求 3a﹣2n的立方根.
20.(8分)21.如图,在平面直角坐标系 xOy中,点 A的坐标为(﹣4,4),
点 B的坐标为(﹣2,0),点 C的坐标为(﹣1,2).
(1)请画出△ABC关于 y轴的对称图形△A1B1C1;
(2)直接写出 A1,B1,C1三点的坐标;
(3)求△ABC的面积.
{#{QQABKLQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
21.(6分)已知实数 a,b的对应点在数轴上的位置如图所示.
(1)判断正负,用“>”“<”填空:b+a 0,﹣a+b 0.
(2)化简: .
22.(8 分)在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
所挂物 0 1 2 3 4 5 6 7 8
体的质
量/千克
弹簧的 12 12.5 13 13.5 14 14.5 15 15.5 16
长度/cm
(1)弹簧不挂物体时的长度是 cm,当所悬挂重物为 3千克时,弹簧的长度为 cm;
(2)如果用 x表示弹性限度内物体的质量,用 y表示弹簧的长度,求出 y与 x的关系式 ;
(3)如果弹簧最大挂重量为 25千克,你能预测当挂重为 14千克时,弹簧的长度是多少?
23.(8分)已知一次函数 y=2x+2.
(1)点 P(2,m)在函数的图象上,求 m的值.
(2)一次函数的图象与 x轴、y轴分别交于点 A、B.求点 A、B的坐标.
(3)已知 C(3,0),求三角形 ABC的面积.
24.(8分)甲骑电动车,乙骑自行车从公园门口出发沿同一路线匀速游玩,甲、乙两人距出发点的路程 S(km)与乙
行驶的时间 x(h)的关系如图①所示,其中 l1表示甲运动的图象,甲、乙两人之间的路程差 y(km)与乙行驶
的时间 x(h)的关系如图②所示,请你解决以下问题:
(1)图②中的自变量是 ,因变量是 ;
(2)甲的速度是 km/h,乙的速度是 km/h;
(3)结合题意和图①,可知图②中:a= ,b= ;
(4)求乙出发多长时间后,甲、乙两人的路程差为 7.5km.
{#{QQABLKQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
1
25.(12分)如图,在平面直角坐标系中,直线 y x 2分别与 x轴、y轴相交于点 A、点 B,直线 CE与 AB相
2
交于点 C(2,m),与 x轴相交于点 D,与 y轴相交于点 E(0,-1),点 P是 x轴上一动点.
(1)求直线 CE的表达式;
(2)求△BCE的面积;
(3)当△CDP的面积等于△BCE面积的一半时,请求出点 P的坐标.
26.(12分)“数形结合”和“建模思想”是数学中的两个很重要的思想方法,先阅读以下材料,然后解答后面的问
题.
例:求代数式 的最小值.
分析: 和 是勾股定理的形式, 是直角边分别是 x和 3的直角三角形的斜边,
是直角边分别是 12﹣x和 2的直角三角形的斜边,因此,我们构造两个直角△ABC和△DEF,
并使直角边 BC和 EF在同一直线上(图 1),向右平移直角△ABC使点 B和 E重合(图 2),这时 CF=x+12﹣x
=12,AC=3,DF=2,问题就变成“点 B在线段 CF的何处时,AB+DB最短?”根据两点间线段最短,得到线
段 AD就是它们的最小值.
回答下面问题:
(1)代数式 的最小值为 ;
(2)变式训练:求代数式 的最小值;
(3)拓展练习:解方程 (利用几何方法解答).
{#{QQABKLQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
一、选择题(共 10 小题,每小题 4 分,共 40 分)
1.下列选项中,y不是 x函数的是( )
A. B. C. D.
2.下列说法正确的是( )
A.16的算术平方根是±4 B.任何数都有两个平方根
C.因为 3的平方是 9,所以 9的平方根是 3 D.﹣1是 1的平方根
3.下列运算正确的是( )
A. B. C. D.
4.若代数式 有意义,则 x的取值范围是( )
A. B. C. D.
5.平面直角坐标系中,点 P(﹣2,3)关于 x轴对称,得到的点的坐标为( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(3,﹣2)
6. 的整数部分为 m,小数部分为 n,则 m﹣n的值为( )
A. B. C. D.
7.下列变量之间的关系,一个变量是另一个变量的正比例函数关系的是( )
A.圆的面积 S随半径 r的变化而变化
B.用 10m长的绳子围成一个矩形,其中一边长 y随它邻边 x的变化而变化
C.正方形的周长 C 随边长 a 的变化而变化
D.汽车油箱中有汽油 50L,行驶过程中邮箱中的油量 Q 随行驶路程 s的变化而变化
8.若函数 y=(k﹣1)x+(k﹣2)的图象经过第一、三、四象限,则 k的取值范围是( )
A.k>1 B.k>2 C.1<k<2 D.k<1
9.如图所示的“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的,如果小正
方形的面积为 6,大正方形的面积为 14,直角三角形中较短直角边的长为 a,较长直角边
的长为 b,那么 ab的值为( )
A.4 B.6 C. D.
10.数轴上表示 ,π的点分别为 A,B,点 A是 BC的中点,则点 C所表示的数是( )
A. B. C. D.
{#{QQABKLQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
二、填空题(共 6 小题,每小题 4 分,共 24 分)
11.(﹣2)2的平方根是 , 的算术平方根是 , 的立方根是 .
12.已知点 A(﹣3,2m﹣4)在 x轴上,点 B(n+3,4)在 y轴上,则 m+n= .
13.已知点 M(2,3),直线 MN∥x轴,且 MN=3,则点 N的坐标是 .
14.点 A(1,y1)、B(2,y2)在一次函数 y=3x+1的图象上,则 y1 y2(用“<”、“=”或“>”填空).
15.已知函数 是关于 x的一次函数,则 m的值是 .
16.如图,在平面直角坐标系中,过点 A(0,4)的直线 a⊥y轴,M(9,4)为直线 a上一点.点 P从点 M出发,
以每秒 2个单位长度的速度沿直线 a向左移动;同时,点 Q从原点出发,以每秒 1个单位长度的速度沿 x轴向
右移动.若以 A,O,Q,P为顶点的四边形的面积是 10,则点 P的坐标为 .
三、解答题(共 11 小题)
17.(12分)计算
(1) (2)
(3) (4) .
18.(6分)求下列各式中的 x.
(1)3x2﹣12=0 (2)(x﹣1)3=﹣64
19.(6分)已知 3m+1的平方根是±5,5n﹣m的立方根是 3.
(1)求 m﹣n的平方根;
(2)若 4a+m的算术平方根是 4,求 3a﹣2n的立方根.
20.(8分)21.如图,在平面直角坐标系 xOy中,点 A的坐标为(﹣4,4),
点 B的坐标为(﹣2,0),点 C的坐标为(﹣1,2).
(1)请画出△ABC关于 y轴的对称图形△A1B1C1;
(2)直接写出 A1,B1,C1三点的坐标;
(3)求△ABC的面积.
{#{QQABKLQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
21.(6分)已知实数 a,b的对应点在数轴上的位置如图所示.
(1)判断正负,用“>”“<”填空:b+a 0,﹣a+b 0.
(2)化简: .
22.(8 分)在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
所挂物 0 1 2 3 4 5 6 7 8
体的质
量/千克
弹簧的 12 12.5 13 13.5 14 14.5 15 15.5 16
长度/cm
(1)弹簧不挂物体时的长度是 cm,当所悬挂重物为 3千克时,弹簧的长度为 cm;
(2)如果用 x表示弹性限度内物体的质量,用 y表示弹簧的长度,求出 y与 x的关系式 ;
(3)如果弹簧最大挂重量为 25千克,你能预测当挂重为 14千克时,弹簧的长度是多少?
23.(8分)已知一次函数 y=2x+2.
(1)点 P(2,m)在函数的图象上,求 m的值.
(2)一次函数的图象与 x轴、y轴分别交于点 A、B.求点 A、B的坐标.
(3)已知 C(3,0),求三角形 ABC的面积.
24.(8分)甲骑电动车,乙骑自行车从公园门口出发沿同一路线匀速游玩,甲、乙两人距出发点的路程 S(km)与乙
行驶的时间 x(h)的关系如图①所示,其中 l1表示甲运动的图象,甲、乙两人之间的路程差 y(km)与乙行驶
的时间 x(h)的关系如图②所示,请你解决以下问题:
(1)图②中的自变量是 ,因变量是 ;
(2)甲的速度是 km/h,乙的速度是 km/h;
(3)结合题意和图①,可知图②中:a= ,b= ;
(4)求乙出发多长时间后,甲、乙两人的路程差为 7.5km.
{#{QQABLKQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
1
25.(12分)如图,在平面直角坐标系中,直线 y x 2分别与 x轴、y轴相交于点 A、点 B,直线 CE与 AB相
2
交于点 C(2,m),与 x轴相交于点 D,与 y轴相交于点 E(0,-1),点 P是 x轴上一动点.
(1)求直线 CE的表达式;
(2)求△BCE的面积;
(3)当△CDP的面积等于△BCE面积的一半时,请求出点 P的坐标.
26.(12分)“数形结合”和“建模思想”是数学中的两个很重要的思想方法,先阅读以下材料,然后解答后面的问
题.
例:求代数式 的最小值.
分析: 和 是勾股定理的形式, 是直角边分别是 x和 3的直角三角形的斜边,
是直角边分别是 12﹣x和 2的直角三角形的斜边,因此,我们构造两个直角△ABC和△DEF,
并使直角边 BC和 EF在同一直线上(图 1),向右平移直角△ABC使点 B和 E重合(图 2),这时 CF=x+12﹣x
=12,AC=3,DF=2,问题就变成“点 B在线段 CF的何处时,AB+DB最短?”根据两点间线段最短,得到线
段 AD就是它们的最小值.
回答下面问题:
(1)代数式 的最小值为 ;
(2)变式训练:求代数式 的最小值;
(3)拓展练习:解方程 (利用几何方法解答).
{#{QQABKLQQAs5ogICwggAISJACAAQQ4KhCUU0WwGqCaCUEqQCkQIIkhBLGeAgMCSgQgGCABBKAAQoKAiIANACFBKNA=A}B#C} A=}#}
同课章节目录
