北师大版四年级下册数学数 图形的学问 课件(共17张PPT)
文档属性
| 名称 | 北师大版四年级下册数学数 图形的学问 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 07:36:24 | ||
图片预览




文档简介
(共17张PPT)
第3课时 数图形的学问
数 学 好 玩
鼹鼠是一种生活在地下的小动物,它的拉丁文学名就是“掘土”的意思,它们每天到处挖洞,捷克斯洛伐克的经典儿童文学《鼹鼠的故事》就讲述了一只胖乎乎的小鼹鼠每天各种各样神奇的经历,构成了一个又一个温馨的小故事。这节课,我们和鼹鼠又将一起经历什么呢?
有多少条不同的路线可以选择呢?想一想,说一说。
鼹鼠钻洞。
任选一个洞口进入,向前走,再任选一个洞口钻出来。
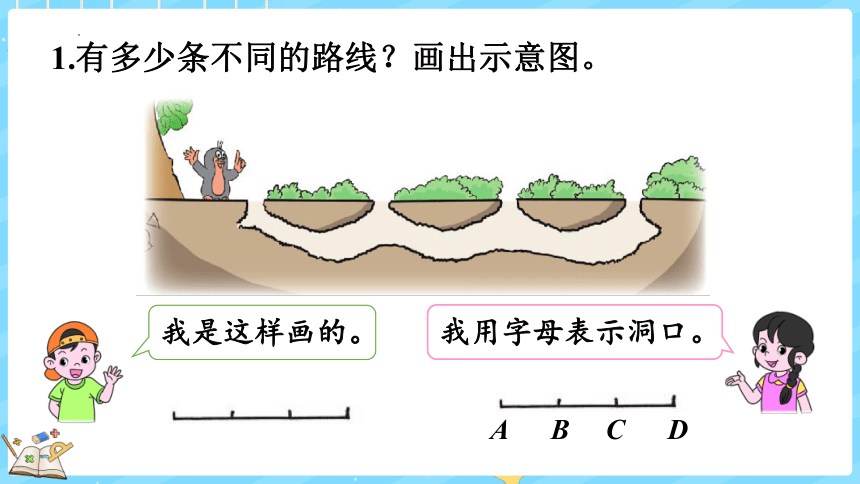
1.有多少条不同的路线?画出示意图。
我是这样画的。
我用字母表示洞口。
A B C D
A
B
C
D
先数短的线段:
再数比较长的线段:
最后数最长的线段:
AB、BC、CD,
AC、BD,
AD。
3+2+1=6(条)
答:一共有6条不同的路线。
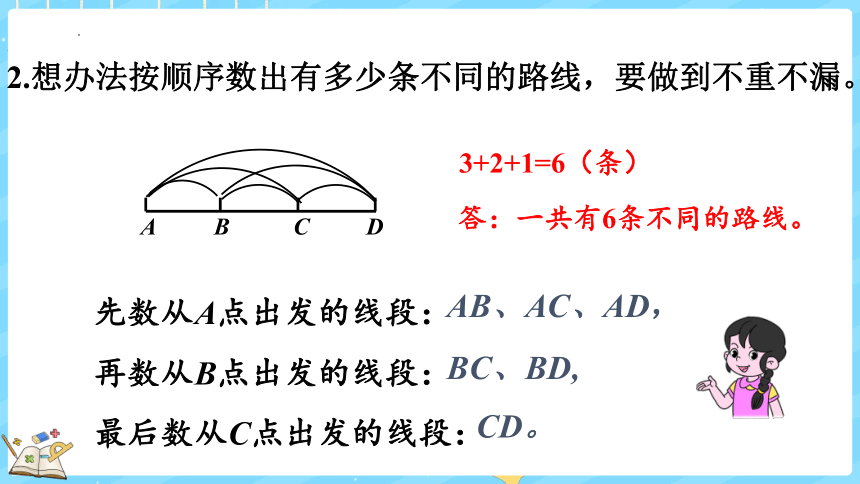
2.想办法按顺序数出有多少条不同的路线,要做到不重不漏。
A
B
C
D
先数从A点出发的线段:
再数从B点出发的线段:
最后数从C点出发的线段:
AB、AC、AD,
BC、BD,
CD。
3+2+1=6(条)
答:一共有6条不同的路线。
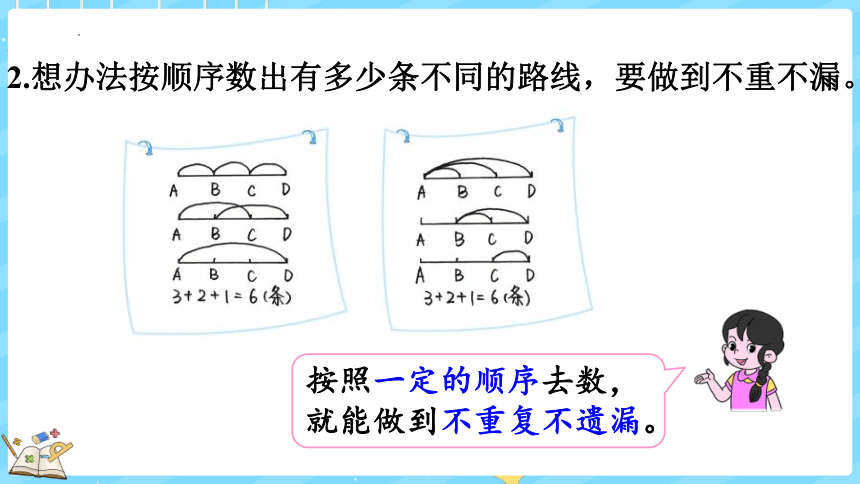
2.想办法按顺序数出有多少条不同的路线,要做到不重不漏。
按照一定的顺序去数,就能做到不重复不遗漏。
2.想办法按顺序数出有多少条不同的路线,要做到不重不漏。
菜地旅行。
单程需要准备多少种不同的车票?
A
B
C
D
E
1.根据情境画出示意图,有顺序地数一数,说说你是
怎样数的。
我是这样数的,一共有10种。
我是这样数的,一共有10种。
4+3+2+1=10(种)
2.如果有6个汽车站,单程需要准备多少种不同的车票呢?
画出图后,重新数一数。
可以接着数下去,在5个汽车站结果的基础上,再加上5。
5+4+3+2+1=15(种)
3.如果有7个汽车站,单程需要准备多少种不同的车票呢?
8个呢?你发现了什么?
有7个汽车站时,最短的线段就有6条,从6开始加到1。
5个站时,车票种数为:4+3+2+1。
6个站时,车票种数为:5+4+3+2+1。
7个站时,车票种数为:6+5+4+3+2+1。
8个站时,车票种数为:7+6+5+4+3+2+1。
有什么规律吗?
我发现:若一条线上有n个点(n为大于1的整数),则共有1+2+3+4+5…+(n-1)条线段。
3.如果有7个汽车站,单程需要准备多少种不同的车票呢?
8个呢?你发现了什么?
1.数出下面图形中有多少条线段?
5+4+3+2+1=15(条)
2.小明过生日,他邀请了4个朋友来吃晚饭,如果每
两个人握一次手,那么他们一共要握多少次手?
4+3+2+1=10(次)
答:他们一共要握10次手。
小明
这节课有什么收获呢?
数线段的方法有两种:一是按照长度数;二是按照线段端点的位置数。
若一条线上有n个点(n为大于1的整数),则共有1+2+3+4+5…+(n-1)条线段。
了解自己生活的城市中,常坐的公交车,一共有几个站点,单程需要准备多少种不同的车票?
5个站:4+3+2+1
6个站:5+4+3+2+1
7个站:6+5+4+3+2+1
8个站:7+6+5+4+3+2+1
有n个点的线上,线段数量= 1+2+3+4+5…+(n-1)
数图形的学问
A
B
C
D
第3课时 数图形的学问
数 学 好 玩
鼹鼠是一种生活在地下的小动物,它的拉丁文学名就是“掘土”的意思,它们每天到处挖洞,捷克斯洛伐克的经典儿童文学《鼹鼠的故事》就讲述了一只胖乎乎的小鼹鼠每天各种各样神奇的经历,构成了一个又一个温馨的小故事。这节课,我们和鼹鼠又将一起经历什么呢?
有多少条不同的路线可以选择呢?想一想,说一说。
鼹鼠钻洞。
任选一个洞口进入,向前走,再任选一个洞口钻出来。
1.有多少条不同的路线?画出示意图。
我是这样画的。
我用字母表示洞口。
A B C D
A
B
C
D
先数短的线段:
再数比较长的线段:
最后数最长的线段:
AB、BC、CD,
AC、BD,
AD。
3+2+1=6(条)
答:一共有6条不同的路线。
2.想办法按顺序数出有多少条不同的路线,要做到不重不漏。
A
B
C
D
先数从A点出发的线段:
再数从B点出发的线段:
最后数从C点出发的线段:
AB、AC、AD,
BC、BD,
CD。
3+2+1=6(条)
答:一共有6条不同的路线。
2.想办法按顺序数出有多少条不同的路线,要做到不重不漏。
按照一定的顺序去数,就能做到不重复不遗漏。
2.想办法按顺序数出有多少条不同的路线,要做到不重不漏。
菜地旅行。
单程需要准备多少种不同的车票?
A
B
C
D
E
1.根据情境画出示意图,有顺序地数一数,说说你是
怎样数的。
我是这样数的,一共有10种。
我是这样数的,一共有10种。
4+3+2+1=10(种)
2.如果有6个汽车站,单程需要准备多少种不同的车票呢?
画出图后,重新数一数。
可以接着数下去,在5个汽车站结果的基础上,再加上5。
5+4+3+2+1=15(种)
3.如果有7个汽车站,单程需要准备多少种不同的车票呢?
8个呢?你发现了什么?
有7个汽车站时,最短的线段就有6条,从6开始加到1。
5个站时,车票种数为:4+3+2+1。
6个站时,车票种数为:5+4+3+2+1。
7个站时,车票种数为:6+5+4+3+2+1。
8个站时,车票种数为:7+6+5+4+3+2+1。
有什么规律吗?
我发现:若一条线上有n个点(n为大于1的整数),则共有1+2+3+4+5…+(n-1)条线段。
3.如果有7个汽车站,单程需要准备多少种不同的车票呢?
8个呢?你发现了什么?
1.数出下面图形中有多少条线段?
5+4+3+2+1=15(条)
2.小明过生日,他邀请了4个朋友来吃晚饭,如果每
两个人握一次手,那么他们一共要握多少次手?
4+3+2+1=10(次)
答:他们一共要握10次手。
小明
这节课有什么收获呢?
数线段的方法有两种:一是按照长度数;二是按照线段端点的位置数。
若一条线上有n个点(n为大于1的整数),则共有1+2+3+4+5…+(n-1)条线段。
了解自己生活的城市中,常坐的公交车,一共有几个站点,单程需要准备多少种不同的车票?
5个站:4+3+2+1
6个站:5+4+3+2+1
7个站:6+5+4+3+2+1
8个站:7+6+5+4+3+2+1
有n个点的线上,线段数量= 1+2+3+4+5…+(n-1)
数图形的学问
A
B
C
D
