21.3 实际问题与一元二次方程 同步培优训练(含答案) 2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 21.3 实际问题与一元二次方程 同步培优训练(含答案) 2024-2025学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 137.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 00:00:00 | ||
图片预览




文档简介
21.3 实际问题与一元二次方程
任务一 传播问题
母题1 有一个人患了流感,经过两轮传染后共有169个人患了流感,每轮传染中平均一个人传染了几个人 设每轮传染中平均一个人传染了x个人,则下列方程正确的为 ( )
A.1+2x=169
B.1+x2=169
C.1+x+x(1+x)=169
D.1+x+x2=169
变式练1:学校“自然之美”研究小组在野外考察时发现了一种植物的生长规律,即植物的1个主干上长出x个枝干,每个枝干又长出x个小分支,现在1个主干上的主干、枝干、小分支的数量之和为73.根据题意,下列方程正确的是 ( )
A.1+(1+x)2=73
B.1+x2=73
C.1+x+x2=73
D.x+(1+x)2=73
任务二 增长率问题
母题2 “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700 kg的目标,第三阶段实现水稻亩产量1008 kg的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率.
(2)按照(1)中亩产量的增长率,科研团队期望第四阶段水稻亩产量达到1200 kg,请通过计算说明他们的目标能否实现.
【关键点拨】
设亩产量的平均增长率为x.
第一阶段亩产量/kg 第二阶段亩产量/kg 第三阶段亩产量/kg
700 700(1+x) 700(1+x)(1+x)=700(1+x)2
变式练2:某蔬菜基地要把一定量的蔬菜租车送往某地,这些蔬菜中1.4吨已经打包好,其余需要立即打包.工作人员第1小时打包15吨,技术熟练后平均每小时打包速度的增长率相同,第3小时打包21.6吨,恰好3小时完成打包任务.
(1)求工作人员平均每小时打包速度的增长率.
(2)共运送的蔬菜是多少吨
任务三 销售问题
母题3 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:该商品的售价每降1元,每星期可多卖出20件.已知该商品的进价为每件40元,在顾客得实惠的前提下,商家若还想获得6080元的利润,应将销售单价定为多少元
【关键点拨】
单件利润/元 销量/件 总利润/元
降价前 60-40 300
降价后(方法一:设销售单价降低x元) 60-x-40 300+20x (60-x-40)(300+20x)=6080
降价后(方法二:设将销售单价定为x元) x-40 300+20·(60-x) (x-40)·[300+20(60-x)]=6080
变式练3:某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产76件,每件的利润为10元.每提高一个档次,每件的利润增加2元,但一天少生产4件.若生产某档次的产品一天的总利润为1080元,求该产品的质量档次.
任务四 利用一元二次方程进行可行性分析
母题4 李明准备进行如下操作试验:把一根长为40 cm的铁丝剪成两段,并把每段首尾相连,各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗 请说明理由.
变式练4:如图,在△ABC中,AB=6 cm,BC=7 cm,∠ABC=30°,点P从A点出发,以1 cm/s的速度向B点移动,点Q从B点出发,以2 cm/s的速度向C点移动,当一个点到达终点时,另一个点也随即停止运动.如果P,Q两点同时出发,几秒后,△PBQ的面积等于4 cm2
任务五 面积问题
母题5 如图,某小区有一块长为30 m,宽为24 m的矩形空地,并计划在其中修建两块相同的矩形绿地,若要使它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米
变式练5:一个包装盒的表面展开图如图所示,设包装盒的高为x cm.
(1)若此包装盒的容积为1125 cm3,请列出关于x的方程,并求出x的值.
(2)是否存在这样的x的值,使得此包装盒的容积为1800 cm3 若存在,请求出相应的x的值;若不存在,请说明理由.
任务六 利用一元二次方程解决动态问题
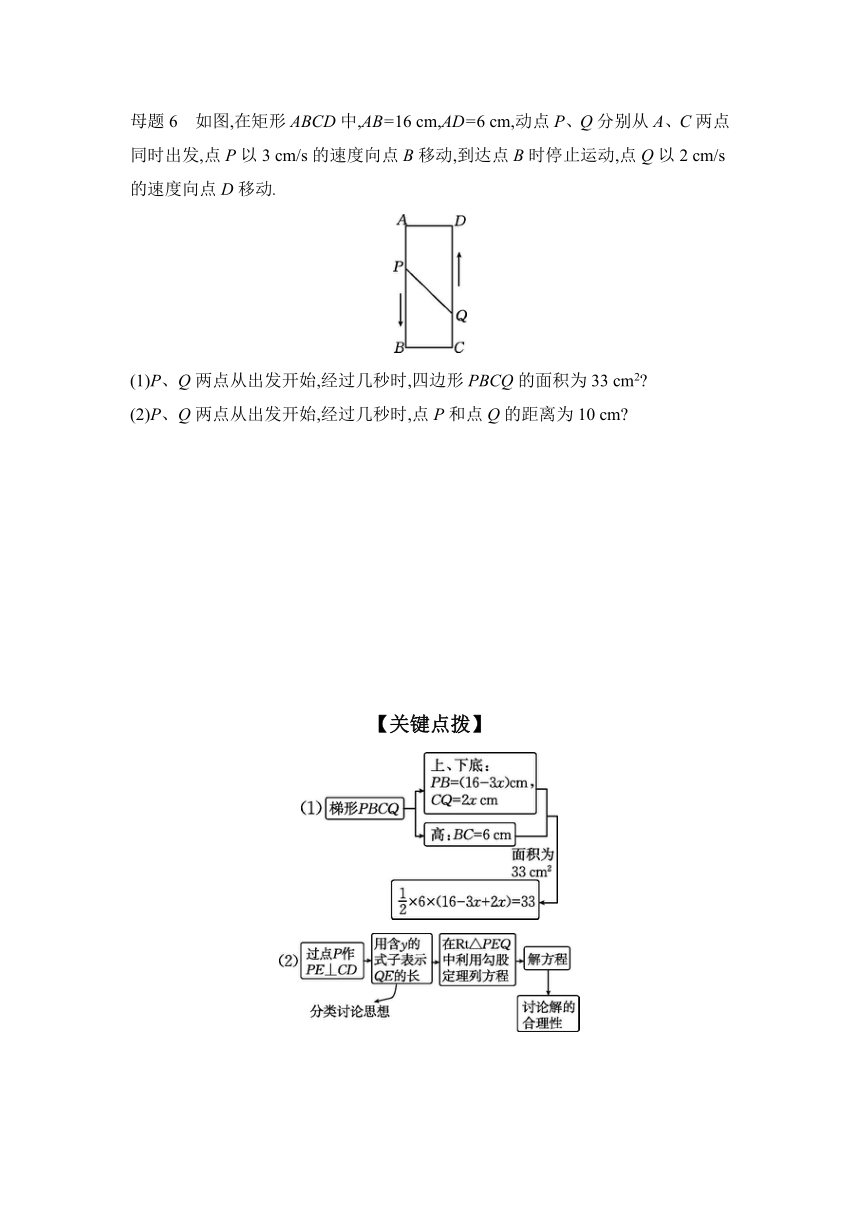
母题6 如图,在矩形ABCD中,AB=16 cm,AD=6 cm,动点P、Q分别从A、C两点同时出发,点P以3 cm/s的速度向点B移动,到达点B时停止运动,点Q以2 cm/s的速度向点D移动.
(1)P、Q两点从出发开始,经过几秒时,四边形PBCQ的面积为33 cm2
(2)P、Q两点从出发开始,经过几秒时,点P和点Q的距离为10 cm
【关键点拨】
变式练6:如图,在△ABC中,∠C=90°,AC=8 cm,BC=4 cm,一动点P从点C出发沿着CB方向以1 cm/s的速度运动,另一动点Q从点A出发沿着AC方向以2 cm/s的速度运动,P,Q两点同时出发,运动时间为t s.
(1)若△PCQ的面积是△ABC面积的,求t的值.
(2)△PCQ的面积能否为△ABC面积的一半 若能,求出t的值;若不能,说明理由.
任务七 利用一元二次方程解决规律探究问题
母题7 在某会议场馆的建设过程中,为了美化地面,选用相同规格的黑、白两色的正方形瓷砖铺设长方形地面,观察如图所示的图形,并解答下列问题:
(1)按上述铺设方案,若铺一块长方形地面共用了506块瓷砖,求此时n的值.
(2)是否存在黑瓷砖块数与白瓷砖块数相等的情形 请通过计算说明理由.
变式练7:某天课上,老师带领同学们利用棋子构图研究数字规律,将一些棋子按如图所示的规律摆放:
第1个图中有7个棋子,第2个图中有11个棋子,第3个图中有17个棋子……按此规律依次递增.
(1)第5个图中有 个棋子;第n个图中有 个棋子.
(2)第n个图中的棋子个数能是115吗 如果能,求出n的值;如果不能,请说明理由.
参考答案
母题1 C 提示:∵每轮传染中平均一个人传染了x个人,
∴第一轮传染中有x个人被传染,第二轮传染中有x(1+x)个人被传染.
又∵有一个人患了流感,经过两轮传染后共有169个人患了流感,
∴可列出方程1+x+x(1+x)=169.
故选C.
变式练1 C
母题2 解:(1)设亩产量的平均增长率为x.
依题意,得700(1+x)2=1008,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:亩产量的平均增长率为20%.
(2)1008×(1+20%)=1209.6(kg).
∵1209.6>1200,
∴他们的目标能实现.
变式练2 解:(1)设工作人员平均每小时打包速度的增长率为x.
根据题意,得15(1+x)2=21.6,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:工作人员平均每小时打包速度的增长率是20%.
(2)第2小时打包的数量为15×(1+20%)=18(吨).
共运送的蔬菜为1.4+15+18+21.6=56(吨).
答:共运送的蔬菜是56吨.
母题3 解:设每件降价x元.
依题意得(60-x-40)(300+20x)=6080,
整理得x2-5x+4=0,
解得x1=4,x2=1,
要使顾客得实惠,则x=4,
60-4=56(元).
答:应将销售单价定为56元.
变式练3 解:设该产品的质量档次为x.
依题意得[10+2(x-1)][76-4(x-1)]=1080,
整理得x2-16x+55=0,
解得x1=5,x2=11.
∵1≤x≤10,∴x=5.
答:该产品的质量档次为5.
母题4 解:(1)设剪成的较短的铁丝的长为x cm,则较长的铁丝的长为(40-x)cm.
由题意,得
+=58,
解得x1=12,x2=28.
当x=12时,较长的铁丝的长为40-12=28(cm);
当x=28时,较长的铁丝的长为40-28=12(cm),12<28(舍去).
答:李明应该把铁丝剪成12 cm和28 cm的两段.
(2)李明的说法正确.理由:
设剪成的较短的铁丝的长为m cm,则较长的铁丝的长为(40-m)cm.
由题意,得+=48,
整理得m2-40m+416=0.
∵Δ=(-40)2-4×416=-64<0,
∴原方程无实数根,
∴李明的说法正确,这两个正方形的面积之和不可能等于48 cm2.
变式练4 解:如图,
过点Q作QE⊥PB于点E,则∠QEB=90°.
∵∠ABC=30°,
∴2QE=QB,
∴S△PBQ=·PB·QE.
设t s后△PBQ的面积等于4 cm2,
则PB=(6-t)cm,QB=2t cm,QE=t cm.
根据题意,得·(6-t)·t=4,
整理得t2-6t+8=0,
解得t1=2,t2=4.
当t=4时,2t=8,8>7,不合题意,舍去,取t=2.
答:2 s后,△PBQ的面积等于4 cm2.
母题5 解:设人行通道的宽度为x m,将两块矩形绿地合在一起后的长为(30-3x)m,宽为(24-2x)m,
由题意得(30-3x)·(24-2x)=480,
整理得x2-22x+40=0,
解得x1=2,x2=20.
当x=20时,30-3x=-30,24-2x=-16,
不符合题意,舍去,∴x=2.
答:人行通道的宽度为2米.
变式练5 解:(1)根据题意得15x(20-x)=1125,
整理得x2-20x+75=0,
解得x1=15,x2=5.
答:x的值为15或5.
(2)不存在.理由:
根据题意得15x(20-x)=1800,
整理得x2-20x+120=0,
Δ=(-20)2-4×1×120=-80<0,
∴此方程无实数根,
∴不存在相应的x的值,使得包装盒的容积为1800 cm3.
母题6 解:(1)设经过x s时,四边形PBCQ的面积为33 cm2.
依题意得×6×(16-3x+2x)=33,
解得x=5.
答:经过5 s时,四边形PBCQ的面积为33 cm2.
(2)设经过y s时,点P和点Q的距离为10 cm.
依题意得62+(16-3y-2y)2=102,
解得y1=1.6,y2=4.8.
答:经过1.6 s或4.8 s时,点P和点Q的距离为10 cm.
变式练6 解:(1)∵S△PCQ=t(8-2t),S△ABC=×4×8=16(cm2),
∴t(8-2t)=16×,
整理得t2-4t+4=0,解得t=2.
答:当t的值为2时,△PCQ的面积是△ABC面积的.
(2)当S△PCQ=S△ABC时,
t(8-2t)=16×,整理得t2-4t+8=0,
Δ=(-4)2-4×1×8=-16<0,
∴此方程没有实数根,
∴△PCQ的面积不可能是△ABC面积的一半.
母题7 解:(1)由题意,得(n+3)(n+2)=506,
∴n2+5n-500=0,
解得n1=20,n2=-25(不合题意,舍去).
答:此时n的值为20.
(2)图形中黑瓷砖的数量为(n+2)(n+3)-n(n+1),
白瓷砖的数量为n(n+1).
当黑、白瓷砖块数相等时,(n+2)(n+3)-n(n+1)=n(n+1),
整理得n2-3n-6=0,解得n1=,n2=.
由题意可知n为整数,故不存在黑瓷砖块数与白瓷砖块数相等的情形.
变式练7 解:(1)35;(n2+n+5).
(2)能.
令n2+n+5=115,
解得n1=-11(不合题意,舍去),n2=10,
∴第10个图中的棋子个数为115.
任务一 传播问题
母题1 有一个人患了流感,经过两轮传染后共有169个人患了流感,每轮传染中平均一个人传染了几个人 设每轮传染中平均一个人传染了x个人,则下列方程正确的为 ( )
A.1+2x=169
B.1+x2=169
C.1+x+x(1+x)=169
D.1+x+x2=169
变式练1:学校“自然之美”研究小组在野外考察时发现了一种植物的生长规律,即植物的1个主干上长出x个枝干,每个枝干又长出x个小分支,现在1个主干上的主干、枝干、小分支的数量之和为73.根据题意,下列方程正确的是 ( )
A.1+(1+x)2=73
B.1+x2=73
C.1+x+x2=73
D.x+(1+x)2=73
任务二 增长率问题
母题2 “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700 kg的目标,第三阶段实现水稻亩产量1008 kg的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率.
(2)按照(1)中亩产量的增长率,科研团队期望第四阶段水稻亩产量达到1200 kg,请通过计算说明他们的目标能否实现.
【关键点拨】
设亩产量的平均增长率为x.
第一阶段亩产量/kg 第二阶段亩产量/kg 第三阶段亩产量/kg
700 700(1+x) 700(1+x)(1+x)=700(1+x)2
变式练2:某蔬菜基地要把一定量的蔬菜租车送往某地,这些蔬菜中1.4吨已经打包好,其余需要立即打包.工作人员第1小时打包15吨,技术熟练后平均每小时打包速度的增长率相同,第3小时打包21.6吨,恰好3小时完成打包任务.
(1)求工作人员平均每小时打包速度的增长率.
(2)共运送的蔬菜是多少吨
任务三 销售问题
母题3 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:该商品的售价每降1元,每星期可多卖出20件.已知该商品的进价为每件40元,在顾客得实惠的前提下,商家若还想获得6080元的利润,应将销售单价定为多少元
【关键点拨】
单件利润/元 销量/件 总利润/元
降价前 60-40 300
降价后(方法一:设销售单价降低x元) 60-x-40 300+20x (60-x-40)(300+20x)=6080
降价后(方法二:设将销售单价定为x元) x-40 300+20·(60-x) (x-40)·[300+20(60-x)]=6080
变式练3:某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产76件,每件的利润为10元.每提高一个档次,每件的利润增加2元,但一天少生产4件.若生产某档次的产品一天的总利润为1080元,求该产品的质量档次.
任务四 利用一元二次方程进行可行性分析
母题4 李明准备进行如下操作试验:把一根长为40 cm的铁丝剪成两段,并把每段首尾相连,各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗 请说明理由.
变式练4:如图,在△ABC中,AB=6 cm,BC=7 cm,∠ABC=30°,点P从A点出发,以1 cm/s的速度向B点移动,点Q从B点出发,以2 cm/s的速度向C点移动,当一个点到达终点时,另一个点也随即停止运动.如果P,Q两点同时出发,几秒后,△PBQ的面积等于4 cm2
任务五 面积问题
母题5 如图,某小区有一块长为30 m,宽为24 m的矩形空地,并计划在其中修建两块相同的矩形绿地,若要使它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米
变式练5:一个包装盒的表面展开图如图所示,设包装盒的高为x cm.
(1)若此包装盒的容积为1125 cm3,请列出关于x的方程,并求出x的值.
(2)是否存在这样的x的值,使得此包装盒的容积为1800 cm3 若存在,请求出相应的x的值;若不存在,请说明理由.
任务六 利用一元二次方程解决动态问题
母题6 如图,在矩形ABCD中,AB=16 cm,AD=6 cm,动点P、Q分别从A、C两点同时出发,点P以3 cm/s的速度向点B移动,到达点B时停止运动,点Q以2 cm/s的速度向点D移动.
(1)P、Q两点从出发开始,经过几秒时,四边形PBCQ的面积为33 cm2
(2)P、Q两点从出发开始,经过几秒时,点P和点Q的距离为10 cm
【关键点拨】
变式练6:如图,在△ABC中,∠C=90°,AC=8 cm,BC=4 cm,一动点P从点C出发沿着CB方向以1 cm/s的速度运动,另一动点Q从点A出发沿着AC方向以2 cm/s的速度运动,P,Q两点同时出发,运动时间为t s.
(1)若△PCQ的面积是△ABC面积的,求t的值.
(2)△PCQ的面积能否为△ABC面积的一半 若能,求出t的值;若不能,说明理由.
任务七 利用一元二次方程解决规律探究问题
母题7 在某会议场馆的建设过程中,为了美化地面,选用相同规格的黑、白两色的正方形瓷砖铺设长方形地面,观察如图所示的图形,并解答下列问题:
(1)按上述铺设方案,若铺一块长方形地面共用了506块瓷砖,求此时n的值.
(2)是否存在黑瓷砖块数与白瓷砖块数相等的情形 请通过计算说明理由.
变式练7:某天课上,老师带领同学们利用棋子构图研究数字规律,将一些棋子按如图所示的规律摆放:
第1个图中有7个棋子,第2个图中有11个棋子,第3个图中有17个棋子……按此规律依次递增.
(1)第5个图中有 个棋子;第n个图中有 个棋子.
(2)第n个图中的棋子个数能是115吗 如果能,求出n的值;如果不能,请说明理由.
参考答案
母题1 C 提示:∵每轮传染中平均一个人传染了x个人,
∴第一轮传染中有x个人被传染,第二轮传染中有x(1+x)个人被传染.
又∵有一个人患了流感,经过两轮传染后共有169个人患了流感,
∴可列出方程1+x+x(1+x)=169.
故选C.
变式练1 C
母题2 解:(1)设亩产量的平均增长率为x.
依题意,得700(1+x)2=1008,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:亩产量的平均增长率为20%.
(2)1008×(1+20%)=1209.6(kg).
∵1209.6>1200,
∴他们的目标能实现.
变式练2 解:(1)设工作人员平均每小时打包速度的增长率为x.
根据题意,得15(1+x)2=21.6,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:工作人员平均每小时打包速度的增长率是20%.
(2)第2小时打包的数量为15×(1+20%)=18(吨).
共运送的蔬菜为1.4+15+18+21.6=56(吨).
答:共运送的蔬菜是56吨.
母题3 解:设每件降价x元.
依题意得(60-x-40)(300+20x)=6080,
整理得x2-5x+4=0,
解得x1=4,x2=1,
要使顾客得实惠,则x=4,
60-4=56(元).
答:应将销售单价定为56元.
变式练3 解:设该产品的质量档次为x.
依题意得[10+2(x-1)][76-4(x-1)]=1080,
整理得x2-16x+55=0,
解得x1=5,x2=11.
∵1≤x≤10,∴x=5.
答:该产品的质量档次为5.
母题4 解:(1)设剪成的较短的铁丝的长为x cm,则较长的铁丝的长为(40-x)cm.
由题意,得
+=58,
解得x1=12,x2=28.
当x=12时,较长的铁丝的长为40-12=28(cm);
当x=28时,较长的铁丝的长为40-28=12(cm),12<28(舍去).
答:李明应该把铁丝剪成12 cm和28 cm的两段.
(2)李明的说法正确.理由:
设剪成的较短的铁丝的长为m cm,则较长的铁丝的长为(40-m)cm.
由题意,得+=48,
整理得m2-40m+416=0.
∵Δ=(-40)2-4×416=-64<0,
∴原方程无实数根,
∴李明的说法正确,这两个正方形的面积之和不可能等于48 cm2.
变式练4 解:如图,
过点Q作QE⊥PB于点E,则∠QEB=90°.
∵∠ABC=30°,
∴2QE=QB,
∴S△PBQ=·PB·QE.
设t s后△PBQ的面积等于4 cm2,
则PB=(6-t)cm,QB=2t cm,QE=t cm.
根据题意,得·(6-t)·t=4,
整理得t2-6t+8=0,
解得t1=2,t2=4.
当t=4时,2t=8,8>7,不合题意,舍去,取t=2.
答:2 s后,△PBQ的面积等于4 cm2.
母题5 解:设人行通道的宽度为x m,将两块矩形绿地合在一起后的长为(30-3x)m,宽为(24-2x)m,
由题意得(30-3x)·(24-2x)=480,
整理得x2-22x+40=0,
解得x1=2,x2=20.
当x=20时,30-3x=-30,24-2x=-16,
不符合题意,舍去,∴x=2.
答:人行通道的宽度为2米.
变式练5 解:(1)根据题意得15x(20-x)=1125,
整理得x2-20x+75=0,
解得x1=15,x2=5.
答:x的值为15或5.
(2)不存在.理由:
根据题意得15x(20-x)=1800,
整理得x2-20x+120=0,
Δ=(-20)2-4×1×120=-80<0,
∴此方程无实数根,
∴不存在相应的x的值,使得包装盒的容积为1800 cm3.
母题6 解:(1)设经过x s时,四边形PBCQ的面积为33 cm2.
依题意得×6×(16-3x+2x)=33,
解得x=5.
答:经过5 s时,四边形PBCQ的面积为33 cm2.
(2)设经过y s时,点P和点Q的距离为10 cm.
依题意得62+(16-3y-2y)2=102,
解得y1=1.6,y2=4.8.
答:经过1.6 s或4.8 s时,点P和点Q的距离为10 cm.
变式练6 解:(1)∵S△PCQ=t(8-2t),S△ABC=×4×8=16(cm2),
∴t(8-2t)=16×,
整理得t2-4t+4=0,解得t=2.
答:当t的值为2时,△PCQ的面积是△ABC面积的.
(2)当S△PCQ=S△ABC时,
t(8-2t)=16×,整理得t2-4t+8=0,
Δ=(-4)2-4×1×8=-16<0,
∴此方程没有实数根,
∴△PCQ的面积不可能是△ABC面积的一半.
母题7 解:(1)由题意,得(n+3)(n+2)=506,
∴n2+5n-500=0,
解得n1=20,n2=-25(不合题意,舍去).
答:此时n的值为20.
(2)图形中黑瓷砖的数量为(n+2)(n+3)-n(n+1),
白瓷砖的数量为n(n+1).
当黑、白瓷砖块数相等时,(n+2)(n+3)-n(n+1)=n(n+1),
整理得n2-3n-6=0,解得n1=,n2=.
由题意可知n为整数,故不存在黑瓷砖块数与白瓷砖块数相等的情形.
变式练7 解:(1)35;(n2+n+5).
(2)能.
令n2+n+5=115,
解得n1=-11(不合题意,舍去),n2=10,
∴第10个图中的棋子个数为115.
同课章节目录
