22.1 二次函数的图象和性质 同步培优训练(含答案)2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 22.1 二次函数的图象和性质 同步培优训练(含答案)2024-2025学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 309.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:13:36 | ||
图片预览



文档简介
22.1 二次函数的图象和性质
任务一 利用二次函数的性质比较大小
母题1 若A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x+c图象上的三点,则y1,y2,y3的大小关系是 ( )
A.y2C.y3变式练1:已知二次函数y=x2-2x+c的图象经过点P(-1,y1)和点Q(m,y2).若y1A.-1B.1C.m<-1或m>3
D.m<-1
任务二 确定二次函数的最大(小)值
子任务1 在实数范围内求二次函数的最值
母题2 用配方法求二次函数y=-2x2+4x-1的最大值.
变式练2:如图,这是二次函数y=x2+bx+c的图象,该函数的最小值是 .
子任务2 在规定范围内求二次函数的最值
母题3 已知函数y=x2-2x-3,当自变量x在下列取值范围内时,分别求函数的最大值和最小值:
(1)-1≤x≤2;
(2)2≤x≤3.
变式练3:已知二次函数y=-x2-2x+3,当a≤x≤时,函数值y的最小值为1,则a的值为 .
任务三 利用抛物线的对称性解决问题
母题4 二次函数y=ax2+bx+c的部分对应值如下表:
x…-3-20135…
y…70-8-9-57…
二次函数y=ax2+bx+c的图象的对称轴为直线x= ,x=2对应的函数值y= .
变式练4:如图,抛物线y=ax2+bx+c与x轴相交于点A、点B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
任务四 二次函数图象的平移变换
子任务1 根据平移过程确定函数图象对应的解析式
母题5 将抛物线y=ax2+bx+c向右平移3个单位长度,再向下平移2个单位长度,得到抛物线y=x2+2x+3,求a,b,c的值.
变式练5:一个二次函数的图象如图所示,将该函数图象先向左平移2个单位长度,再向下平移1个单位长度得到新函数的图象,求出新函数的解析式.
子任务2 根据抛物线平移的特点求图形的面积
母题6 如图,抛物线与y轴交于点A(0,3),顶点为P(-2,2).若平移该抛物线使其顶点P沿直线移动到点P'(2,-2),点A的对应点为A',则抛物线上PA段扫过的区域(阴影部分)的面积为 ( )
A.6 B.7 C.8 D.12
【关键点拨】
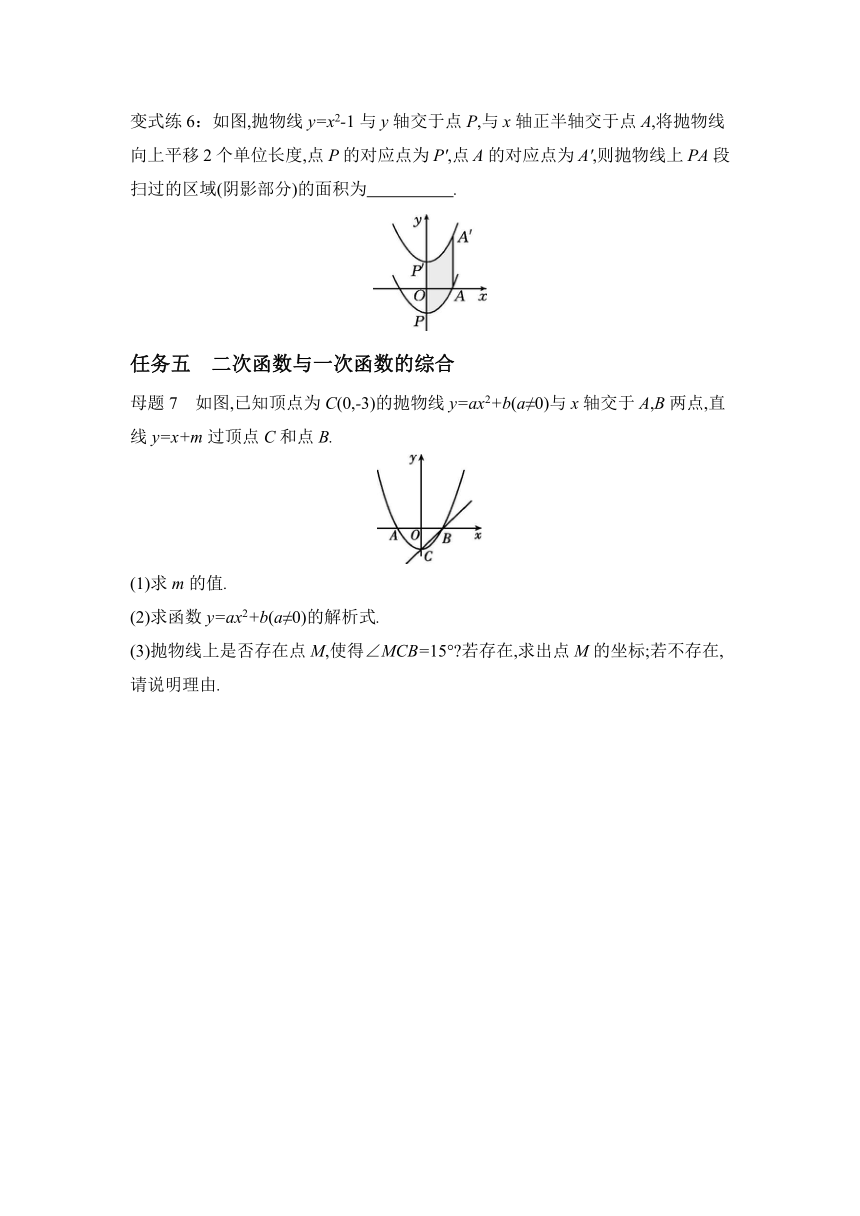
变式练6:如图,抛物线y=x2-1与y轴交于点P,与x轴正半轴交于点A,将抛物线向上平移2个单位长度,点P的对应点为P',点A的对应点为A',则抛物线上PA段扫过的区域(阴影部分)的面积为 .
任务五 二次函数与一次函数的综合
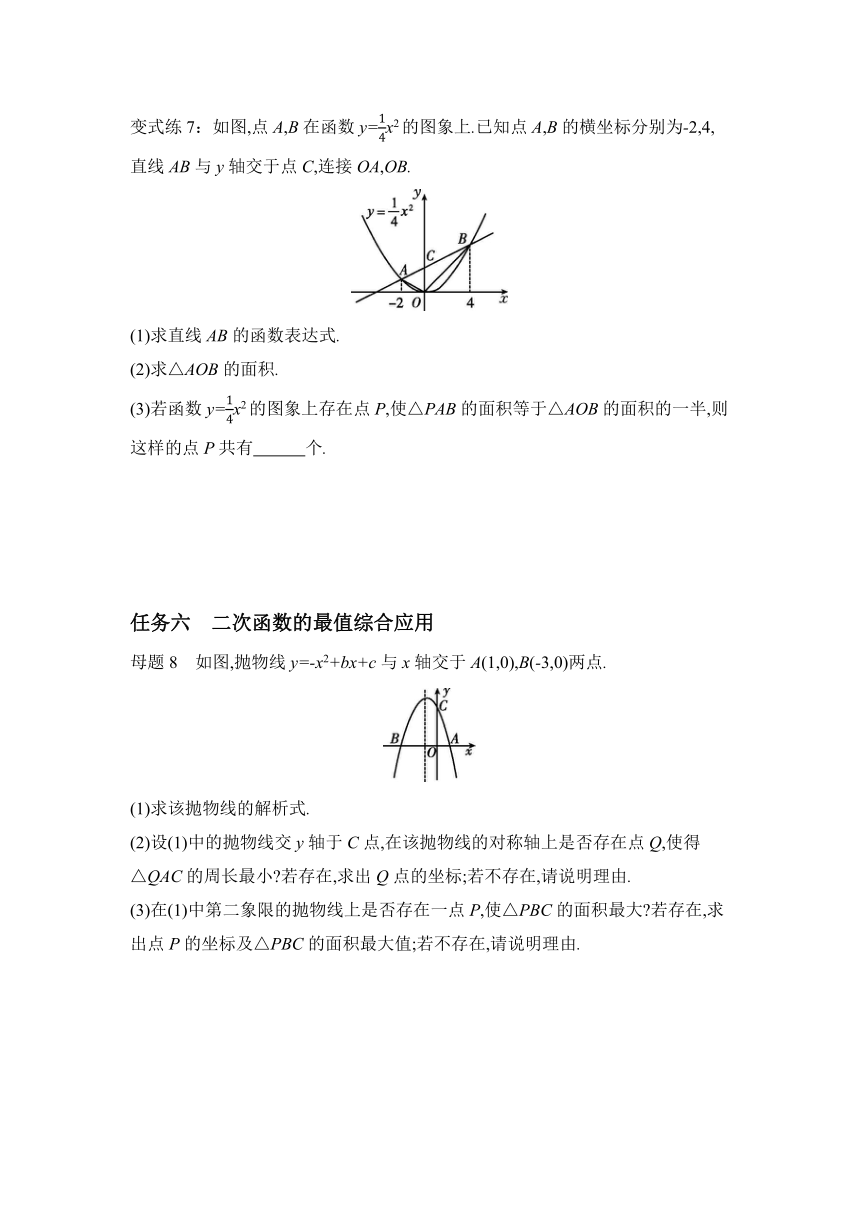
母题7 如图,已知顶点为C(0,-3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.
(1)求m的值.
(2)求函数y=ax2+b(a≠0)的解析式.
(3)抛物线上是否存在点M,使得∠MCB=15° 若存在,求出点M的坐标;若不存在,请说明理由.
变式练7:如图,点A,B在函数y=x2的图象上.已知点A,B的横坐标分别为-2,4,直线AB与y轴交于点C,连接OA,OB.
(1)求直线AB的函数表达式.
(2)求△AOB的面积.
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 个.
任务六 二次函数的最值综合应用
母题8 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式.
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小 若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在(1)中第二象限的抛物线上是否存在一点P,使△PBC的面积最大 若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由.
变式练8:如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式.
(2)请在对称轴上找一点M,使AM+CM最小,求出点M的坐标.
(3)若P是直线BC下方的抛物线上一动点(不与点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.连接PB,PC,求△PBC的面积最大时点P的坐标.
任务七 二次函数的综合探究问题
母题9 如图,抛物线经过A(-1,0),B(5,0),C0,-三点.
(1)求抛物线的解析式.
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标.
(3)M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形 若存在,直接写出点N的坐标;若不存在,请说明理由.
变式练9:如图,抛物线y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),M是抛物线的顶点.
(1)求抛物线的解析式.
(2)P是线段MB上一个动点,且点P的横坐标为m,过点P作PD⊥x轴于点D,交抛物线于点E,求线段PE的最大值,并求出此时点E的坐标.
(3)在(2)的条件下,若在线段MB上存在点P,使得△PCD为直角三角形,请直接写出点P的坐标.
参考答案
母题1 A 提示:∵y=x2+2x+c=(x+1)2+c-1,
∴抛物线开口向上,对称轴为直线x=-1.
∵A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x+c图象上的三点,
∴C(3,y3)关于直线x=-1的对称点(-5,y3)在二次函数y=x2+2x+c的图象上.
∵-5<-4<-3<-1,
∴y3>y1>y2.
故选A.
变式练1 C 提示:∵二次函数y=x2-2x+c,
∴图象的开口向上,对称轴为直线x=-=1,
∴当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,
∴点P(-1,y1)关于对称轴的对称点为(3,y1).
∵二次函数y=x2-2x+c的图象经过点P(-1,y1)和点Q(m,y2),且y1∴m<-1或m>3.
故选C.
母题2 解:y=-2x2+4x-1
=-2(x2-2x)-1
=-2(x-1)2+1,
则二次函数y=-2x2+4x-1的最大值为1.
变式练2 -4 提示:由函数图象可得-=-=-1,
解得b=2.
∵图象经过点(-3,0),
∴0=(-3)2-3×2+c,
解得c=-3,
∴二次函数的解析式为y=x2+2x-3,
则二次函数的最小值为==-4.
故答案为-4.
母题3 解:由y=x2-2x-3=(x-1)2-4,
得图象的对称轴为直线x=1.
(1)∵开口向上,
∴当x=1时,有最小值,最小值是-4.
∵当x=-1时,y=0,当x=2时,y=-3,
∴当x=-1时,y有最大值,最大值是0.
(2)∵在y=(x-1)2-4中,当x>1时,y随x的增大而增大,
∴当x=2时,有最小值,最小值是(2-1)2-4=-3,
当x=3时,有最大值,最大值是(3-1)2-4=0.
变式练3 -1- 提示:∵y=-x2-2x+3=-(x+1)2+4,
∴图象开口向下,顶点坐标为(-1,4).
根据题意,当a≤x≤时,函数值y的最小值为1,
当y=1时,-(x+1)2+4=1,
∴x=-1±.
∵-1+>,
∴-1-≤x≤时,函数值y的最小值为1,
∴a=-1-.
故答案为-1-.
母题4 1;-8
变式练4 (-2,0) 提示:令x=0,得到y=c,
∴C(0,c).
∵D(m,c),∴函数图象的对称轴是直线x=.
设A点坐标为(x,0),由点A,B关于直线x=对称,得=,
解得x=-2,
即A点坐标为(-2,0).
故答案为(-2,0).
母题5 解:∵y=x2+2x+3=(x+1)2+2,
∴y=x2+2x+3向左平移3个单位长度,再向上平移2个单位长度后,
可得y=(x+1+3)2+2+2,即y=(x+4)2+4=x2+8x+20,
∴a=1,b=8,c=20.
变式练5 解:由题图可知该函数为二次函数,对称轴为直线x=-1且过点A(0,3)、点B(1,0).
设该函数的解析式为y=a(x+1)2+k(a≠0),
把A(0,3)、B(1,0)代入y=a(x+1)2+k,得
解得
∴y=-(x+1)2+4.
把函数y=-(x+1)2+4的图象先向左平移2个单位长度,再向下平移1个单位长度,得y=-(x+3)2+3,
∴新函数的解析式为y=-(x+3)2+3.
母题6 D 提示:如图,连接AP,A'P',过点A作AD⊥PP'于点D,
由题意,可得出AP∥A'P',AP=A'P',
∴四边形APP'A'是平行四边形.
∵抛物线的顶点为P(-2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P'(2,-2),
∴易得PO==2,∠AOP=45°,∴易得PP'=2×2=4.
又∵AD⊥OP,
∴△ADO是等腰直角三角形,
∴AD=DO=sin 45°·OA=×3=,
∴抛物线上PA段扫过的区域(阴影部分)的面积为4×=12.
故选D.
变式练6 2 提示:如图,连接AP,A'P'.
当y=0时,x2-1=0,解得x1=1,x2=-1,
∴A(1,0).
∵抛物线y=x2-1向上平移2个单位长度,点P的对应点为P',点A的对应点为A',
∴PP'=AA'=2,
∴抛物线上PA段扫过的区域(阴影部分)的面积=S平行四边形APP'A'=1×2=2.
故答案为2.
母题7 解:(1)将(0,-3)代入y=x+m,解得m=-3.
(2)将y=0代入y=x-3,解得x=3,所以点B的坐标为(3,0).
将(0,-3),(3,0)代入y=ax2+b(a≠0),
可得解得a=,b=-3,
所以函数的解析式为y=x2-3.
(3)存在点M,使得∠MCB=15°.
分两种情况:
①如图,若点M在点B上方,设MC交x轴于点D,则∠ODC=45°+15°=60°,
则OD=.
设直线DC的方程为y=kx-3,代入(,0),可得k=,
联立方程组
解得x=0,y=-3或x=3,y=6,
∴M1(3,6).
②如图,若点M在点B下方,设MC交x轴于点E,则∠OEC=45°-15°=30°,
∴OE=3.
设直线EC的方程为y=kx-3,代入点(3,0),可得k=,
联立方程组解得x=0,y=-3或x=,y=-2,
∴M2(,-2).
故抛物线上存在点M(3,6)或(,-2),使得∠MCB=15°.
变式练7 解:(1)∵点A,B在函数y=x2的图象上,A,B的横坐标分别为-2,4,
∴A(-2,1),B(4,4).
设直线AB的函数表达式为y=kx+b,
∴解得
∴直线AB的函数表达式为y=x+2.
(2)在y=x+2中,令x=0,则y=2,
∴C点的坐标为(0,2),∴OC=2,
∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=6.
(3)4.
提示:如图,过OC的中点作AB的平行线交抛物线于点P1,P2,
此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半,作直线P1P2关于直线AB的对称直线,交抛物线于点P3,P4,此时△P3AB的面积和△P4AB的面积于△AOB的面积的一半,
所以这样的点P共有4个.
故答案为4.
母题8 解:(1)把A(1,0),B(-3,0)分别代入y=-x2+bx+c,得
解得∴抛物线的解析式为y=-x2-2x+3.
(2)存在.理由如下:
由题知A,B两点关于抛物线的对称轴x=-1对称,
∴直线BC与直线x=-1的交点即为Q点,此时△AQC的周长最小,如图1所示.
∵y=-x2-2x+3,∴C的坐标为(0,3),
∴直线BC的解析式为y=x+3.
由解得∴Q(-1,2).
(3)存在.理由如下:
设点P(x,-x2-2x+3)(-3S△BPC=S四边形BPCO-S△BOC=S四边形BPCO-,若S四边形BPCO有最大值,则此时S△BPC最大.
如图2,过点P作PE垂直于x轴,
∴S四边形BPCO=S△BPE+S直角梯形PEOC
=BE·PE+OE(PE+OC)
=(x+3)(-x2-2x+3)+(-x)(-x2-2x+3+3)
=-x+2++,
当x=-时,S四边形BPCD的最大值=+,
∴S△BPC的最大值=+-=.
当x=-时,-x2-2x+3=,∴点P的坐标为-,.
变式练8 解:(1)∵抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C,
∴y=a(x-1)(x-3)=ax2-4ax+3a,
∴3a=3,即a=1,
∴抛物线解析式为y=x2-4x+3.
(2)由y=x2-4x+3可知,对称轴为直线x=2,C(0,3),
由抛物线的对称性可知,点A和点B关于对称轴对称,连接BC与对称轴交点即为M,如图1所示.
将点B(3,0),C(0,3)代入直线BC解析式y=kx+b,
则
解得k=-1,b=3,
∴直线BC解析式为yBC=-x+3,
∴M(2,1).
(3)设P(m,m2-4m+3),
如图2,过点P作y轴的平行线交直线BC于点D,
∴D(m,-m+3),
∴PD=(-m+3)-(m2-4m+3)=-m2+3m,
∴S△PBC=S△CPD+S△BPD
=OB·PD
=-m2+m
=-m-2+,
∴当m=时,S有最大值.
当m=时,m2-4m+3=-.
∴P,-,
∴△PBC的面积最大时点P的坐标为,-.
母题9 解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0).
∵A(-1,0),B(5,0),C0,-三点在抛物线上,
∴解得
∴抛物线的解析式为y=x2-2x-.
(2)如图1,连接BC,与抛物线的对称轴的交点为点P,连接AP.
∵抛物线的解析式为y=x2-2x-,
∴其对称轴为直线x=-=-=2.
设直线BC的解析式为y=kx+b(k≠0),且过B(5,0),C0,-,
∴解得∴直线BC的解析式为y=x-.
当x=2时,y=1-=-,
∴点P的坐标为2,-.
(3)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.
①如图2,当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C0,-,
∴N14,-;
②当点N在x轴上方时,
如图2,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
∴△AN2D≌△M2CO(ASA),
∴N2D=OC=,即N2点的纵坐标为,
∴x2-2x-=,解得x=2+或x=2-,
∴N22+,,N32-,.
综上所述,符合条件的点N的坐标为4,-或2+,或2-,.
变式练9 解:(1)把B(3,0),C(0,3)代入y=-x2+bx+c,
得解得
∴抛物线的解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴M(1,4).
设直线BM的解析式为y=kx+n,
把B(3,0),M(1,4)代入,
得解得
∴直线BM的解析式为y=-2x+6.
设P(m,-2m+6)(1≤m≤3),
则E(m,-m2+2m+3),
∴PE=-m2+4m-3=-(m-2)2+1,
∵1≤m≤3,
∴当m=2时,PE有最大值,最大值为1,点E的坐标为(2,3).
(3)存在.
∵∠PDC不可能为90°,
∴当∠DPC=90°时,PD=OC=3,即-2m+6=3,解得m=,此时P点坐标为,3;
当∠PCD=90°时,PC2+CD2=PD2,即m2+(-2m+3)2+32+m2=(-2m+6)2,
整理得m2+6m-9=0,解得m1=-3-3(舍去),m2=-3+3.
当m=-3+3时,y=-2m+6=6-6+6=12-6,此时P点坐标为(-3+3,12-6).
综上所述,当P点坐标为,3或(-3+3,12-6)时,△PCD为直角三角形.
任务一 利用二次函数的性质比较大小
母题1 若A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x+c图象上的三点,则y1,y2,y3的大小关系是 ( )
A.y2
D.m<-1
任务二 确定二次函数的最大(小)值
子任务1 在实数范围内求二次函数的最值
母题2 用配方法求二次函数y=-2x2+4x-1的最大值.
变式练2:如图,这是二次函数y=x2+bx+c的图象,该函数的最小值是 .
子任务2 在规定范围内求二次函数的最值
母题3 已知函数y=x2-2x-3,当自变量x在下列取值范围内时,分别求函数的最大值和最小值:
(1)-1≤x≤2;
(2)2≤x≤3.
变式练3:已知二次函数y=-x2-2x+3,当a≤x≤时,函数值y的最小值为1,则a的值为 .
任务三 利用抛物线的对称性解决问题
母题4 二次函数y=ax2+bx+c的部分对应值如下表:
x…-3-20135…
y…70-8-9-57…
二次函数y=ax2+bx+c的图象的对称轴为直线x= ,x=2对应的函数值y= .
变式练4:如图,抛物线y=ax2+bx+c与x轴相交于点A、点B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
任务四 二次函数图象的平移变换
子任务1 根据平移过程确定函数图象对应的解析式
母题5 将抛物线y=ax2+bx+c向右平移3个单位长度,再向下平移2个单位长度,得到抛物线y=x2+2x+3,求a,b,c的值.
变式练5:一个二次函数的图象如图所示,将该函数图象先向左平移2个单位长度,再向下平移1个单位长度得到新函数的图象,求出新函数的解析式.
子任务2 根据抛物线平移的特点求图形的面积
母题6 如图,抛物线与y轴交于点A(0,3),顶点为P(-2,2).若平移该抛物线使其顶点P沿直线移动到点P'(2,-2),点A的对应点为A',则抛物线上PA段扫过的区域(阴影部分)的面积为 ( )
A.6 B.7 C.8 D.12
【关键点拨】
变式练6:如图,抛物线y=x2-1与y轴交于点P,与x轴正半轴交于点A,将抛物线向上平移2个单位长度,点P的对应点为P',点A的对应点为A',则抛物线上PA段扫过的区域(阴影部分)的面积为 .
任务五 二次函数与一次函数的综合
母题7 如图,已知顶点为C(0,-3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.
(1)求m的值.
(2)求函数y=ax2+b(a≠0)的解析式.
(3)抛物线上是否存在点M,使得∠MCB=15° 若存在,求出点M的坐标;若不存在,请说明理由.
变式练7:如图,点A,B在函数y=x2的图象上.已知点A,B的横坐标分别为-2,4,直线AB与y轴交于点C,连接OA,OB.
(1)求直线AB的函数表达式.
(2)求△AOB的面积.
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 个.
任务六 二次函数的最值综合应用
母题8 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式.
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小 若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在(1)中第二象限的抛物线上是否存在一点P,使△PBC的面积最大 若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由.
变式练8:如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式.
(2)请在对称轴上找一点M,使AM+CM最小,求出点M的坐标.
(3)若P是直线BC下方的抛物线上一动点(不与点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.连接PB,PC,求△PBC的面积最大时点P的坐标.
任务七 二次函数的综合探究问题
母题9 如图,抛物线经过A(-1,0),B(5,0),C0,-三点.
(1)求抛物线的解析式.
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标.
(3)M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形 若存在,直接写出点N的坐标;若不存在,请说明理由.
变式练9:如图,抛物线y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),M是抛物线的顶点.
(1)求抛物线的解析式.
(2)P是线段MB上一个动点,且点P的横坐标为m,过点P作PD⊥x轴于点D,交抛物线于点E,求线段PE的最大值,并求出此时点E的坐标.
(3)在(2)的条件下,若在线段MB上存在点P,使得△PCD为直角三角形,请直接写出点P的坐标.
参考答案
母题1 A 提示:∵y=x2+2x+c=(x+1)2+c-1,
∴抛物线开口向上,对称轴为直线x=-1.
∵A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x+c图象上的三点,
∴C(3,y3)关于直线x=-1的对称点(-5,y3)在二次函数y=x2+2x+c的图象上.
∵-5<-4<-3<-1,
∴y3>y1>y2.
故选A.
变式练1 C 提示:∵二次函数y=x2-2x+c,
∴图象的开口向上,对称轴为直线x=-=1,
∴当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,
∴点P(-1,y1)关于对称轴的对称点为(3,y1).
∵二次函数y=x2-2x+c的图象经过点P(-1,y1)和点Q(m,y2),且y1
故选C.
母题2 解:y=-2x2+4x-1
=-2(x2-2x)-1
=-2(x-1)2+1,
则二次函数y=-2x2+4x-1的最大值为1.
变式练2 -4 提示:由函数图象可得-=-=-1,
解得b=2.
∵图象经过点(-3,0),
∴0=(-3)2-3×2+c,
解得c=-3,
∴二次函数的解析式为y=x2+2x-3,
则二次函数的最小值为==-4.
故答案为-4.
母题3 解:由y=x2-2x-3=(x-1)2-4,
得图象的对称轴为直线x=1.
(1)∵开口向上,
∴当x=1时,有最小值,最小值是-4.
∵当x=-1时,y=0,当x=2时,y=-3,
∴当x=-1时,y有最大值,最大值是0.
(2)∵在y=(x-1)2-4中,当x>1时,y随x的增大而增大,
∴当x=2时,有最小值,最小值是(2-1)2-4=-3,
当x=3时,有最大值,最大值是(3-1)2-4=0.
变式练3 -1- 提示:∵y=-x2-2x+3=-(x+1)2+4,
∴图象开口向下,顶点坐标为(-1,4).
根据题意,当a≤x≤时,函数值y的最小值为1,
当y=1时,-(x+1)2+4=1,
∴x=-1±.
∵-1+>,
∴-1-≤x≤时,函数值y的最小值为1,
∴a=-1-.
故答案为-1-.
母题4 1;-8
变式练4 (-2,0) 提示:令x=0,得到y=c,
∴C(0,c).
∵D(m,c),∴函数图象的对称轴是直线x=.
设A点坐标为(x,0),由点A,B关于直线x=对称,得=,
解得x=-2,
即A点坐标为(-2,0).
故答案为(-2,0).
母题5 解:∵y=x2+2x+3=(x+1)2+2,
∴y=x2+2x+3向左平移3个单位长度,再向上平移2个单位长度后,
可得y=(x+1+3)2+2+2,即y=(x+4)2+4=x2+8x+20,
∴a=1,b=8,c=20.
变式练5 解:由题图可知该函数为二次函数,对称轴为直线x=-1且过点A(0,3)、点B(1,0).
设该函数的解析式为y=a(x+1)2+k(a≠0),
把A(0,3)、B(1,0)代入y=a(x+1)2+k,得
解得
∴y=-(x+1)2+4.
把函数y=-(x+1)2+4的图象先向左平移2个单位长度,再向下平移1个单位长度,得y=-(x+3)2+3,
∴新函数的解析式为y=-(x+3)2+3.
母题6 D 提示:如图,连接AP,A'P',过点A作AD⊥PP'于点D,
由题意,可得出AP∥A'P',AP=A'P',
∴四边形APP'A'是平行四边形.
∵抛物线的顶点为P(-2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P'(2,-2),
∴易得PO==2,∠AOP=45°,∴易得PP'=2×2=4.
又∵AD⊥OP,
∴△ADO是等腰直角三角形,
∴AD=DO=sin 45°·OA=×3=,
∴抛物线上PA段扫过的区域(阴影部分)的面积为4×=12.
故选D.
变式练6 2 提示:如图,连接AP,A'P'.
当y=0时,x2-1=0,解得x1=1,x2=-1,
∴A(1,0).
∵抛物线y=x2-1向上平移2个单位长度,点P的对应点为P',点A的对应点为A',
∴PP'=AA'=2,
∴抛物线上PA段扫过的区域(阴影部分)的面积=S平行四边形APP'A'=1×2=2.
故答案为2.
母题7 解:(1)将(0,-3)代入y=x+m,解得m=-3.
(2)将y=0代入y=x-3,解得x=3,所以点B的坐标为(3,0).
将(0,-3),(3,0)代入y=ax2+b(a≠0),
可得解得a=,b=-3,
所以函数的解析式为y=x2-3.
(3)存在点M,使得∠MCB=15°.
分两种情况:
①如图,若点M在点B上方,设MC交x轴于点D,则∠ODC=45°+15°=60°,
则OD=.
设直线DC的方程为y=kx-3,代入(,0),可得k=,
联立方程组
解得x=0,y=-3或x=3,y=6,
∴M1(3,6).
②如图,若点M在点B下方,设MC交x轴于点E,则∠OEC=45°-15°=30°,
∴OE=3.
设直线EC的方程为y=kx-3,代入点(3,0),可得k=,
联立方程组解得x=0,y=-3或x=,y=-2,
∴M2(,-2).
故抛物线上存在点M(3,6)或(,-2),使得∠MCB=15°.
变式练7 解:(1)∵点A,B在函数y=x2的图象上,A,B的横坐标分别为-2,4,
∴A(-2,1),B(4,4).
设直线AB的函数表达式为y=kx+b,
∴解得
∴直线AB的函数表达式为y=x+2.
(2)在y=x+2中,令x=0,则y=2,
∴C点的坐标为(0,2),∴OC=2,
∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=6.
(3)4.
提示:如图,过OC的中点作AB的平行线交抛物线于点P1,P2,
此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半,作直线P1P2关于直线AB的对称直线,交抛物线于点P3,P4,此时△P3AB的面积和△P4AB的面积于△AOB的面积的一半,
所以这样的点P共有4个.
故答案为4.
母题8 解:(1)把A(1,0),B(-3,0)分别代入y=-x2+bx+c,得
解得∴抛物线的解析式为y=-x2-2x+3.
(2)存在.理由如下:
由题知A,B两点关于抛物线的对称轴x=-1对称,
∴直线BC与直线x=-1的交点即为Q点,此时△AQC的周长最小,如图1所示.
∵y=-x2-2x+3,∴C的坐标为(0,3),
∴直线BC的解析式为y=x+3.
由解得∴Q(-1,2).
(3)存在.理由如下:
设点P(x,-x2-2x+3)(-3
如图2,过点P作PE垂直于x轴,
∴S四边形BPCO=S△BPE+S直角梯形PEOC
=BE·PE+OE(PE+OC)
=(x+3)(-x2-2x+3)+(-x)(-x2-2x+3+3)
=-x+2++,
当x=-时,S四边形BPCD的最大值=+,
∴S△BPC的最大值=+-=.
当x=-时,-x2-2x+3=,∴点P的坐标为-,.
变式练8 解:(1)∵抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C,
∴y=a(x-1)(x-3)=ax2-4ax+3a,
∴3a=3,即a=1,
∴抛物线解析式为y=x2-4x+3.
(2)由y=x2-4x+3可知,对称轴为直线x=2,C(0,3),
由抛物线的对称性可知,点A和点B关于对称轴对称,连接BC与对称轴交点即为M,如图1所示.
将点B(3,0),C(0,3)代入直线BC解析式y=kx+b,
则
解得k=-1,b=3,
∴直线BC解析式为yBC=-x+3,
∴M(2,1).
(3)设P(m,m2-4m+3),
如图2,过点P作y轴的平行线交直线BC于点D,
∴D(m,-m+3),
∴PD=(-m+3)-(m2-4m+3)=-m2+3m,
∴S△PBC=S△CPD+S△BPD
=OB·PD
=-m2+m
=-m-2+,
∴当m=时,S有最大值.
当m=时,m2-4m+3=-.
∴P,-,
∴△PBC的面积最大时点P的坐标为,-.
母题9 解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0).
∵A(-1,0),B(5,0),C0,-三点在抛物线上,
∴解得
∴抛物线的解析式为y=x2-2x-.
(2)如图1,连接BC,与抛物线的对称轴的交点为点P,连接AP.
∵抛物线的解析式为y=x2-2x-,
∴其对称轴为直线x=-=-=2.
设直线BC的解析式为y=kx+b(k≠0),且过B(5,0),C0,-,
∴解得∴直线BC的解析式为y=x-.
当x=2时,y=1-=-,
∴点P的坐标为2,-.
(3)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.
①如图2,当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C0,-,
∴N14,-;
②当点N在x轴上方时,
如图2,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
∴△AN2D≌△M2CO(ASA),
∴N2D=OC=,即N2点的纵坐标为,
∴x2-2x-=,解得x=2+或x=2-,
∴N22+,,N32-,.
综上所述,符合条件的点N的坐标为4,-或2+,或2-,.
变式练9 解:(1)把B(3,0),C(0,3)代入y=-x2+bx+c,
得解得
∴抛物线的解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴M(1,4).
设直线BM的解析式为y=kx+n,
把B(3,0),M(1,4)代入,
得解得
∴直线BM的解析式为y=-2x+6.
设P(m,-2m+6)(1≤m≤3),
则E(m,-m2+2m+3),
∴PE=-m2+4m-3=-(m-2)2+1,
∵1≤m≤3,
∴当m=2时,PE有最大值,最大值为1,点E的坐标为(2,3).
(3)存在.
∵∠PDC不可能为90°,
∴当∠DPC=90°时,PD=OC=3,即-2m+6=3,解得m=,此时P点坐标为,3;
当∠PCD=90°时,PC2+CD2=PD2,即m2+(-2m+3)2+32+m2=(-2m+6)2,
整理得m2+6m-9=0,解得m1=-3-3(舍去),m2=-3+3.
当m=-3+3时,y=-2m+6=6-6+6=12-6,此时P点坐标为(-3+3,12-6).
综上所述,当P点坐标为,3或(-3+3,12-6)时,△PCD为直角三角形.
同课章节目录
