22.3 实际问题与二次函数 同步培优训练(含答案)2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数 同步培优训练(含答案)2024-2025学年数学人教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 242.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:15:30 | ||
图片预览





文档简介
22.3 实际问题与二次函数
任务一 利用二次函数求解抛物线形的实际问题
子任务1 抛物线形建筑物问题
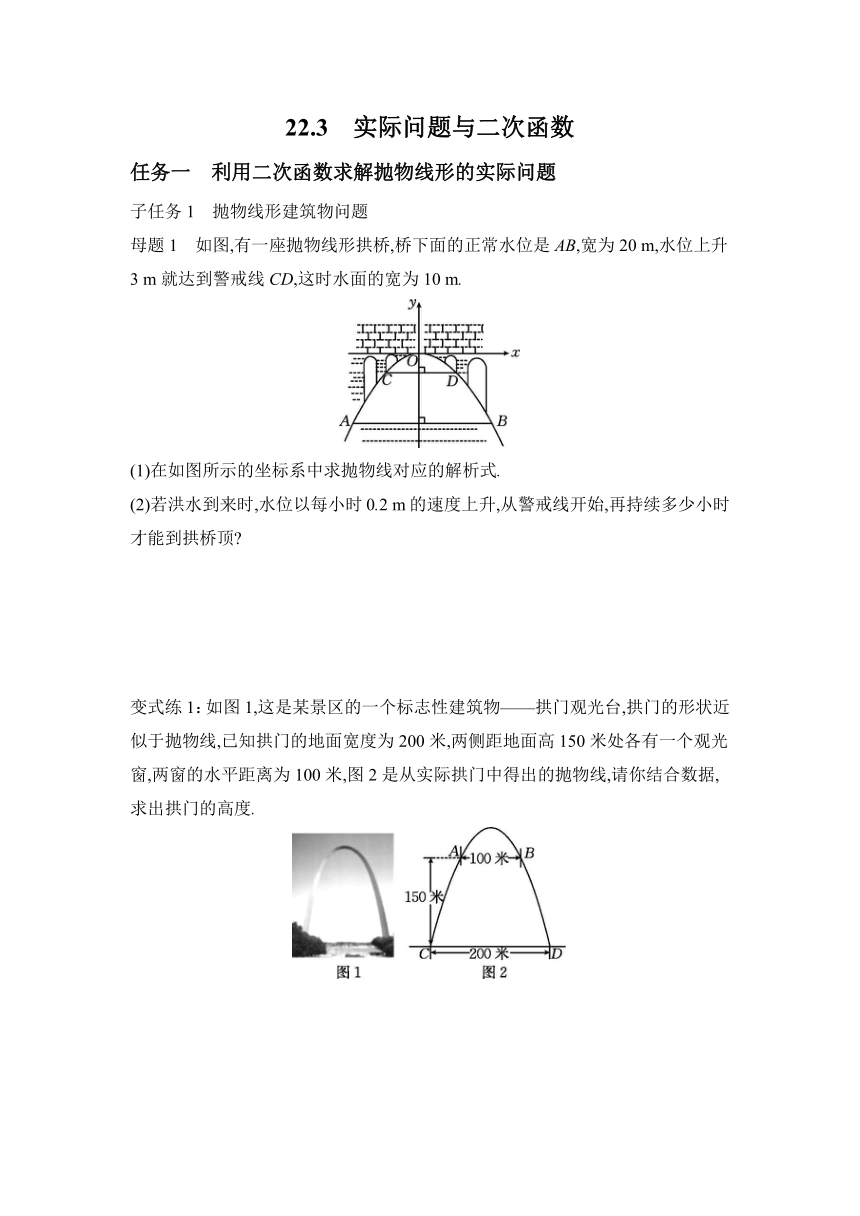
母题1 如图,有一座抛物线形拱桥,桥下面的正常水位是AB,宽为20 m,水位上升3 m就达到警戒线CD,这时水面的宽为10 m.
(1)在如图所示的坐标系中求抛物线对应的解析式.
(2)若洪水到来时,水位以每小时0.2 m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶
变式练1:如图1,这是某景区的一个标志性建筑物——拱门观光台,拱门的形状近似于抛物线,已知拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,图2是从实际拱门中得出的抛物线,请你结合数据,求出拱门的高度.
子任务2 抛物线形运动路线问题
母题2 如图1,排球场长为18 m,宽为9 m,网高为2.24 m,队员站在底线O点处发球,球从点O的正上方1.9 m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m,即BA=2.88m,这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数解析式(不必写出x的取值范围),并判断这次发球能否过网 是否出界 说明理由.
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1 m,边线0.5m),问发球点O在底线上的哪个位置 (参考数据: 取1.4)
变式练2:跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过K点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA为66 m,基准点K到起跳台的水平距离为75 m,高度为h(h为定值)m.设运动员从起跳点A起跳后的高度y(m)与水平距离x(m)之间的函数关系为y=ax2+bx+c(a≠0).
(1)c的值为 .
(2)①若运动员落地点恰好到达K点,且此时a=-,b=,求基准点K的高度h;
②若a=-时,运动员落地点要超过K点,则b的取值范围为 .
(3)若运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,试判断他的落地点能否超过K点,并说明理由.
母题3 为增强学生身体素质,创设体育文化氛围,某校开展田径运动会,小贤同学报了投铅球比赛的项目,如图,曲线AB就是他投出的铅球运动路线,呈抛物线形,出手点A离地面BC的高度为 m,铅球飞行的水平距离的长度为13 m.过A作AO⊥BC于点O,以OB所在直线为x轴,OA所在直线为y轴,建立平面直角坐标系,如图所示.
(1)写出A,B两点的坐标.
(2)若抛物线的解析式为y=ax2+bx+c(a≠0).
①求的取值范围;
②若=-10,求小贤同学投出的铅球运动路线(抛物线)的解析式.
变式练3:某公司为城市广场上一雕塑AB安装喷水装置.喷水口位于雕塑的顶端点B处,喷出的水柱轨迹呈现抛物线形状.据此建立平面直角坐标系,如图.
若喷出的水柱轨迹BC上某一点与支柱AB的水平距离为x(单位:m),与广场地面的垂直高度为y(单位:m).下面的表中记录了y与x的五组数据:
x/m 0 2 6 10
y/m 3
根据上述信息,解决以下问题:
(1)求出y与x之间的函数关系.
(2)求水柱落地点与雕塑AB的水平距离.
(3)为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:在喷出水柱轨迹的形状抛物线y=ax2+bx+c不变的前提下,把水柱喷水的半径(动态喷水时,点C到AB的距离)控制在7 m到14 m之间,请探究改建后喷水池水柱的最大高度和b的取值范围.
任务二 利用二次函数解决动态几何问题
母题4 如图,矩形ABCD的顶点A,B的坐标分别为(-4,0)和(2,0),BC=2.设直线AC与直线x=4交于点E.
(1)求以直线x=4为对称轴,且过点C与原点O的抛物线的函数解析式,并说明此抛物线一定过点E.
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于点C,N之间的一动点,求△CMN面积的最大值.
【关键点拨】
变式练4:在平面直角坐标系中,抛物线y=x2-2mx+m2+2m+2与x轴有两个交点.
(1)当m=-3时,求抛物线与x轴交点的坐标.
(2)过点P(0,m-1)作直线l⊥y轴,抛物线的顶点A在直线l与x轴之间(不包含点A在直线l上的情况),求m的取值范围.
(3)在(2)的条件下,设抛物线的对称轴与直线l相交于点B,当△ABO的面积最大时,求m的值.
参考答案
母题1 解:(1)设所求抛物线对应的解析式为y=ax2(a≠0),
由CD=10 m,可设D(5,b),
由AB=20 m,水位上升3 m就达到警戒线CD,
则B(10,b-3).
把点D,B的坐标分别代入y=ax2,
得
解得
∴y=-x2.
(2)∵b=-1,
∴拱桥顶O到CD的距离为1 m,
∴=5(小时),
∴再持续5小时才能到拱桥顶.
变式练1 解:建立平面直角坐标系如图所示,
此时,抛物线与x轴的交点为C(-100,0),D(100,0).
设这条抛物线的解析式为y=a(x-100)(x+100).
∵抛物线经过点B(50,150),
可得150=a(50-100)(50+100),
解得a=-,
∴抛物线的解析式为y=-(x-100)(x+100).
当x=0时,y=200,
∴拱门的高度为200米.
母题2 解:(1)能过网,但是出界了.理由:设抛物线的解析式为y=a(x-7)2+2.88,
将x=0,y=1.9代入上式并解得a=-,
故抛物线的解析式为y=-(x-7)2+2.88.
当x=9时,y=-(x-7)2+2.88=2.8>2.24;
当x=18时,y=-(x-7)2+2.88=0.46>0,
故这次发球能过网,但是出界了.
(2)如图,分别过点O,P作边线和底线的平行线,且交点为Q,
在Rt△OPQ中,OQ=18-1=17(m),
当y=0时,-(x-7)2+2.88=0,解得x1=19,x2=-5(不合题意,舍去),
∴OP=19 m,
∴PQ=6≈8.4 m.
∵9-8.4-0.5=0.1(m),
∴发球点O在底线上且距另一条边线0.1 m处.
变式练2 解:(1)∵起跳台的高度OA为66 m,
∴A(0,66).
把A(0,66)代入y=ax2+bx+c,
得c=66.
故答案为66.
(2)①∵a=-,b=,
∴y=-x2+x+66.
∵基准点K到起跳台的水平距离为75 m,
∴y=-×752+×75+66=21,
∴基准点K的高度h为21 m.
②∵a=-,
∴y=-x2+bx+66.
∵运动员落地点要超过K点,
∴x=75时,y>21,
即-×752+75b+66>21,
解得b>.
故答案为b>.
(3)他的落地点能超过K点.理由:
∵运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,
∴抛物线的顶点为(25,76).
设抛物线解析式为y=a(x-25)2+76,
把(0,66)代入得66=a(0-25)2+76,
解得a=-,
∴抛物线解析式为y=-(x-25)2+76.
当x=75时,y=-×(75-25)2+76=36,
∵36>21,
∴他的落地点能超过K点.
母题3 解:(1)∵出手点A离地面BC的高度为 m,铅球飞行的水平距离的长度为13 m.
∴A0,,B(13,0).
(2)①∵0<-<13,∴-26<<0.
②∵=-10,∴对称轴为直线x=5.
故该抛物线与x轴的另一个交点为(-3,0).
∴设抛物线的解析式为y=a(x+3)(x-13),
将0,代入上式,得=a(0+3)(0-13),
∴a=-,∴b=.
故小贤同学投出的铅球运动路线的解析式为y=-x2+x+.
变式练3 解:(1)设y与x之间的函数关系为y=ax2+bx+c,把(0,3)2,,6,代入得
解得
∴y=-x2+x+3.
(2)在y=-x2+x+3中,令y=0,得-x2+x+3=0,
解得x=14或x=-2(舍去),
∴水柱落地点与雕塑AB的水平距离是14 m.
(3)∵喷出水柱轨迹的形状不变,
∴a=-,
当水柱喷水的半径为7 m时,抛物线经过点(7,0),(0,3),
∴
解得
∴y=-x2+x+3=-x-2+,
∴当x=时,喷水池水柱的最大高度是 m,
由(2)知,水柱喷水的半径为14 m时,y=-x2+x+3=-(x-6)2+,
∴当x=6时,喷水池水柱的最大高度是 m,
综上所述,喷水池水柱的最大高度是 m,b的范围是≤b≤.
母题4 解:(1)设抛物线的函数解析式为y=a(x-4)2+m,由题意得C(2,2).
∵抛物线过点C与原点O,
∴
解得
∴所求抛物线的函数解析式为y=-(x-4)2+.
当x=4时,y=,即抛物线经过点4,.
设直线AC的函数解析式为y=kx+b,将点A,C的坐标代入,
得
解得
∴直线AC的函数解析式为y=x+,
∴点E的坐标为,
∴此抛物线一定过点E.
(2)如图,过点M作MQ∥y轴,交x轴于点Q,交直线CN于点P.
易知N(8,0),
可得直线CN的解析式为y=-x+.
设点Q的坐标为(n,0),则Pn,-n+,Mn,-n2+n,
∴MP=-n2+n-=-n2+n-.
∴S△CMN=S△CPM+S△MNP=MP·|xM-xC|+MP·|xN-xM|=MP·|xN-xC|=××6=-n2+5n-8,
即S=-(n-5)2+(2∵2<5<8,
∴当n=5时,S△CMN取得最大值,最大值为,
即△CMN面积的最大值为.
变式练4 解:(1)当 m=-3时,y=x2+6x+9-6+2=x2+6x+5,
当y=0时,即 x2+6x+5=0,
解得 x1=-1,x2=-5,
∴抛物线与x轴交点的坐标为(-1,0)和(-5,0).
(2)如图1,
∵抛物线 y=x2-2mx+m2+2m+2 与x轴有两个交点,
∴Δ=4m2-4×1×(m2+2m+2)>0,∴m<-1.
∵y=x2-2mx+m2+2m+2=(x-m)2+2m+2,
∴顶点A的坐标为(m,2m+2).
∵过点P(0,m-1)作直线l⊥y轴,抛物线的顶点A在直线l与x轴之间(不包含点A在直线l上的情况),
∴2m+2>m-1,
∴m>-3.
综上所述,m的取值范围是-3(3)如图2,
∵顶点A的坐标为(m,2m+2),P(0,m-1).
∴AB=2m+2-(m-1)=m+3.
∵△ABO的面积=·AB·PB=·(m+3)·(-m)=-m+2+,
当△ABO的面积最大时,m的值为-.
任务一 利用二次函数求解抛物线形的实际问题
子任务1 抛物线形建筑物问题
母题1 如图,有一座抛物线形拱桥,桥下面的正常水位是AB,宽为20 m,水位上升3 m就达到警戒线CD,这时水面的宽为10 m.
(1)在如图所示的坐标系中求抛物线对应的解析式.
(2)若洪水到来时,水位以每小时0.2 m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶
变式练1:如图1,这是某景区的一个标志性建筑物——拱门观光台,拱门的形状近似于抛物线,已知拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,图2是从实际拱门中得出的抛物线,请你结合数据,求出拱门的高度.
子任务2 抛物线形运动路线问题
母题2 如图1,排球场长为18 m,宽为9 m,网高为2.24 m,队员站在底线O点处发球,球从点O的正上方1.9 m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m,即BA=2.88m,这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数解析式(不必写出x的取值范围),并判断这次发球能否过网 是否出界 说明理由.
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1 m,边线0.5m),问发球点O在底线上的哪个位置 (参考数据: 取1.4)
变式练2:跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过K点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA为66 m,基准点K到起跳台的水平距离为75 m,高度为h(h为定值)m.设运动员从起跳点A起跳后的高度y(m)与水平距离x(m)之间的函数关系为y=ax2+bx+c(a≠0).
(1)c的值为 .
(2)①若运动员落地点恰好到达K点,且此时a=-,b=,求基准点K的高度h;
②若a=-时,运动员落地点要超过K点,则b的取值范围为 .
(3)若运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,试判断他的落地点能否超过K点,并说明理由.
母题3 为增强学生身体素质,创设体育文化氛围,某校开展田径运动会,小贤同学报了投铅球比赛的项目,如图,曲线AB就是他投出的铅球运动路线,呈抛物线形,出手点A离地面BC的高度为 m,铅球飞行的水平距离的长度为13 m.过A作AO⊥BC于点O,以OB所在直线为x轴,OA所在直线为y轴,建立平面直角坐标系,如图所示.
(1)写出A,B两点的坐标.
(2)若抛物线的解析式为y=ax2+bx+c(a≠0).
①求的取值范围;
②若=-10,求小贤同学投出的铅球运动路线(抛物线)的解析式.
变式练3:某公司为城市广场上一雕塑AB安装喷水装置.喷水口位于雕塑的顶端点B处,喷出的水柱轨迹呈现抛物线形状.据此建立平面直角坐标系,如图.
若喷出的水柱轨迹BC上某一点与支柱AB的水平距离为x(单位:m),与广场地面的垂直高度为y(单位:m).下面的表中记录了y与x的五组数据:
x/m 0 2 6 10
y/m 3
根据上述信息,解决以下问题:
(1)求出y与x之间的函数关系.
(2)求水柱落地点与雕塑AB的水平距离.
(3)为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:在喷出水柱轨迹的形状抛物线y=ax2+bx+c不变的前提下,把水柱喷水的半径(动态喷水时,点C到AB的距离)控制在7 m到14 m之间,请探究改建后喷水池水柱的最大高度和b的取值范围.
任务二 利用二次函数解决动态几何问题
母题4 如图,矩形ABCD的顶点A,B的坐标分别为(-4,0)和(2,0),BC=2.设直线AC与直线x=4交于点E.
(1)求以直线x=4为对称轴,且过点C与原点O的抛物线的函数解析式,并说明此抛物线一定过点E.
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于点C,N之间的一动点,求△CMN面积的最大值.
【关键点拨】
变式练4:在平面直角坐标系中,抛物线y=x2-2mx+m2+2m+2与x轴有两个交点.
(1)当m=-3时,求抛物线与x轴交点的坐标.
(2)过点P(0,m-1)作直线l⊥y轴,抛物线的顶点A在直线l与x轴之间(不包含点A在直线l上的情况),求m的取值范围.
(3)在(2)的条件下,设抛物线的对称轴与直线l相交于点B,当△ABO的面积最大时,求m的值.
参考答案
母题1 解:(1)设所求抛物线对应的解析式为y=ax2(a≠0),
由CD=10 m,可设D(5,b),
由AB=20 m,水位上升3 m就达到警戒线CD,
则B(10,b-3).
把点D,B的坐标分别代入y=ax2,
得
解得
∴y=-x2.
(2)∵b=-1,
∴拱桥顶O到CD的距离为1 m,
∴=5(小时),
∴再持续5小时才能到拱桥顶.
变式练1 解:建立平面直角坐标系如图所示,
此时,抛物线与x轴的交点为C(-100,0),D(100,0).
设这条抛物线的解析式为y=a(x-100)(x+100).
∵抛物线经过点B(50,150),
可得150=a(50-100)(50+100),
解得a=-,
∴抛物线的解析式为y=-(x-100)(x+100).
当x=0时,y=200,
∴拱门的高度为200米.
母题2 解:(1)能过网,但是出界了.理由:设抛物线的解析式为y=a(x-7)2+2.88,
将x=0,y=1.9代入上式并解得a=-,
故抛物线的解析式为y=-(x-7)2+2.88.
当x=9时,y=-(x-7)2+2.88=2.8>2.24;
当x=18时,y=-(x-7)2+2.88=0.46>0,
故这次发球能过网,但是出界了.
(2)如图,分别过点O,P作边线和底线的平行线,且交点为Q,
在Rt△OPQ中,OQ=18-1=17(m),
当y=0时,-(x-7)2+2.88=0,解得x1=19,x2=-5(不合题意,舍去),
∴OP=19 m,
∴PQ=6≈8.4 m.
∵9-8.4-0.5=0.1(m),
∴发球点O在底线上且距另一条边线0.1 m处.
变式练2 解:(1)∵起跳台的高度OA为66 m,
∴A(0,66).
把A(0,66)代入y=ax2+bx+c,
得c=66.
故答案为66.
(2)①∵a=-,b=,
∴y=-x2+x+66.
∵基准点K到起跳台的水平距离为75 m,
∴y=-×752+×75+66=21,
∴基准点K的高度h为21 m.
②∵a=-,
∴y=-x2+bx+66.
∵运动员落地点要超过K点,
∴x=75时,y>21,
即-×752+75b+66>21,
解得b>.
故答案为b>.
(3)他的落地点能超过K点.理由:
∵运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,
∴抛物线的顶点为(25,76).
设抛物线解析式为y=a(x-25)2+76,
把(0,66)代入得66=a(0-25)2+76,
解得a=-,
∴抛物线解析式为y=-(x-25)2+76.
当x=75时,y=-×(75-25)2+76=36,
∵36>21,
∴他的落地点能超过K点.
母题3 解:(1)∵出手点A离地面BC的高度为 m,铅球飞行的水平距离的长度为13 m.
∴A0,,B(13,0).
(2)①∵0<-<13,∴-26<<0.
②∵=-10,∴对称轴为直线x=5.
故该抛物线与x轴的另一个交点为(-3,0).
∴设抛物线的解析式为y=a(x+3)(x-13),
将0,代入上式,得=a(0+3)(0-13),
∴a=-,∴b=.
故小贤同学投出的铅球运动路线的解析式为y=-x2+x+.
变式练3 解:(1)设y与x之间的函数关系为y=ax2+bx+c,把(0,3)2,,6,代入得
解得
∴y=-x2+x+3.
(2)在y=-x2+x+3中,令y=0,得-x2+x+3=0,
解得x=14或x=-2(舍去),
∴水柱落地点与雕塑AB的水平距离是14 m.
(3)∵喷出水柱轨迹的形状不变,
∴a=-,
当水柱喷水的半径为7 m时,抛物线经过点(7,0),(0,3),
∴
解得
∴y=-x2+x+3=-x-2+,
∴当x=时,喷水池水柱的最大高度是 m,
由(2)知,水柱喷水的半径为14 m时,y=-x2+x+3=-(x-6)2+,
∴当x=6时,喷水池水柱的最大高度是 m,
综上所述,喷水池水柱的最大高度是 m,b的范围是≤b≤.
母题4 解:(1)设抛物线的函数解析式为y=a(x-4)2+m,由题意得C(2,2).
∵抛物线过点C与原点O,
∴
解得
∴所求抛物线的函数解析式为y=-(x-4)2+.
当x=4时,y=,即抛物线经过点4,.
设直线AC的函数解析式为y=kx+b,将点A,C的坐标代入,
得
解得
∴直线AC的函数解析式为y=x+,
∴点E的坐标为,
∴此抛物线一定过点E.
(2)如图,过点M作MQ∥y轴,交x轴于点Q,交直线CN于点P.
易知N(8,0),
可得直线CN的解析式为y=-x+.
设点Q的坐标为(n,0),则Pn,-n+,Mn,-n2+n,
∴MP=-n2+n-=-n2+n-.
∴S△CMN=S△CPM+S△MNP=MP·|xM-xC|+MP·|xN-xM|=MP·|xN-xC|=××6=-n2+5n-8,
即S=-(n-5)2+(2
∴当n=5时,S△CMN取得最大值,最大值为,
即△CMN面积的最大值为.
变式练4 解:(1)当 m=-3时,y=x2+6x+9-6+2=x2+6x+5,
当y=0时,即 x2+6x+5=0,
解得 x1=-1,x2=-5,
∴抛物线与x轴交点的坐标为(-1,0)和(-5,0).
(2)如图1,
∵抛物线 y=x2-2mx+m2+2m+2 与x轴有两个交点,
∴Δ=4m2-4×1×(m2+2m+2)>0,∴m<-1.
∵y=x2-2mx+m2+2m+2=(x-m)2+2m+2,
∴顶点A的坐标为(m,2m+2).
∵过点P(0,m-1)作直线l⊥y轴,抛物线的顶点A在直线l与x轴之间(不包含点A在直线l上的情况),
∴2m+2>m-1,
∴m>-3.
综上所述,m的取值范围是-3
∵顶点A的坐标为(m,2m+2),P(0,m-1).
∴AB=2m+2-(m-1)=m+3.
∵△ABO的面积=·AB·PB=·(m+3)·(-m)=-m+2+,
当△ABO的面积最大时,m的值为-.
同课章节目录
