23.1 图形的旋转 同步培优训练(含答案)2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 23.1 图形的旋转 同步培优训练(含答案)2024-2025学年数学人教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 435.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:20:15 | ||
图片预览





文档简介
23.1 图形的旋转
任务一 求旋转图形中相关角度的大小或线段的长度
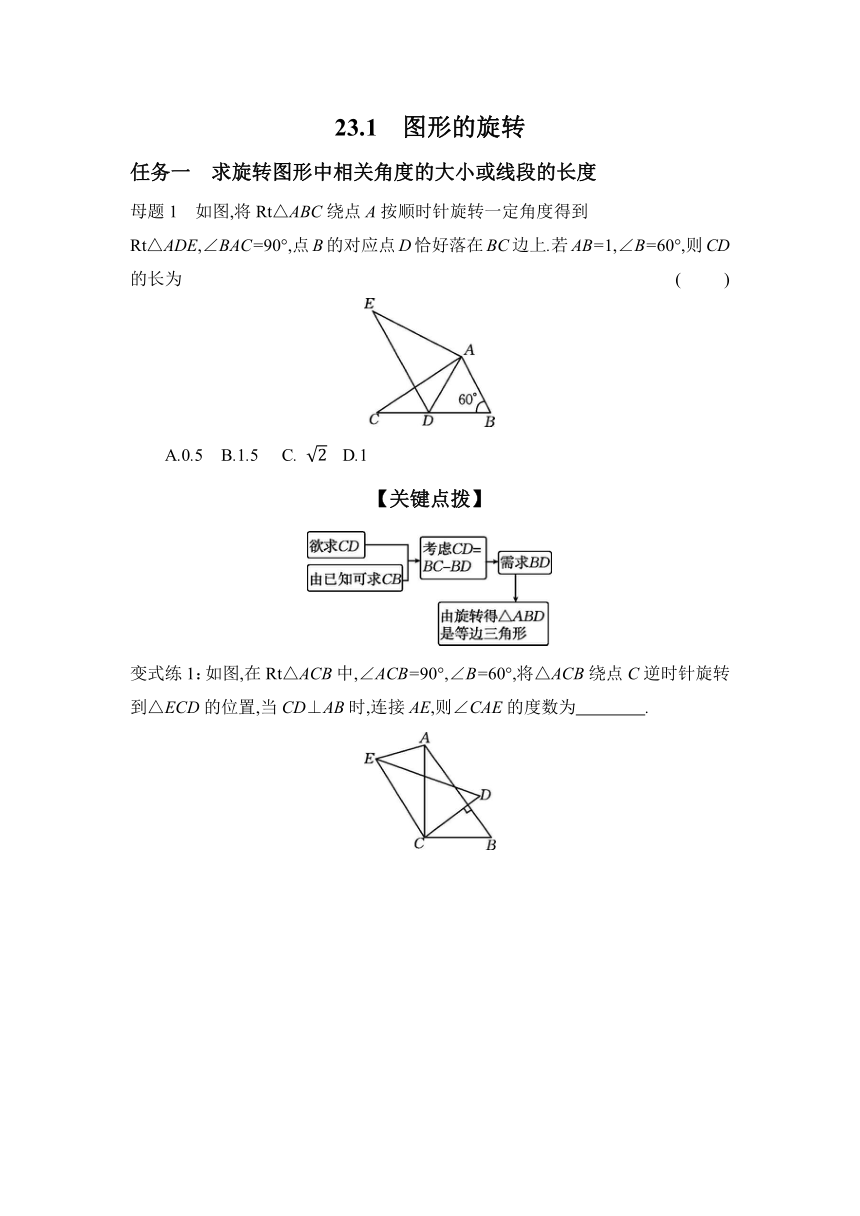
母题1 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,∠BAC=90°,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为 ( )
A.0.5 B.1.5 C. D.1
【关键点拨】
变式练1:如图,在Rt△ACB中,∠ACB=90°,∠B=60°,将△ACB绕点C逆时针旋转到△ECD的位置,当CD⊥AB时,连接AE,则∠CAE的度数为 .
任务二 旋转作图
子任务1 已知旋转中心和一对对应点,求作旋转后的图形
母题2 如图,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定点B,C,D的对应点的位置以及旋转后的四边形.
变式练2:如图,在Rt△ABC中,∠B=90°,将△ABC绕点A顺时针旋转得到△ADE,点B,C的对应点分别为点D,E,点D落在AC边上.尺规作图:作出△ADE(不写作法,保留作图痕迹).
子任务2 平面直角坐标系中的旋转作图
母题3 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1).
(1)把△ABC平移后,其中点A平移到点A1(4,5),在图中画出平移后得到的△A1B1C1,并写出点B1,C1的坐标.
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在图中画出旋转后的△A1B2C2,并写出点B2,C2的坐标.
变式练3:如图,在平面直角坐标系中,△AOB的三个顶点坐标分别为A(1,0),O(0,0),B(2,2).以点O为旋转中心,将△AOB逆时针旋转90°,得到△A1OB1.
(1)画出△A1OB1.
(2)直接写出点A1和点B1的坐标.
(3)求线段AB1的长度.
任务三 利用旋转的性质求阴影部分的面积
母题4 如图,正方形ABCD和正方形EFGO的边长都是2,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积是 ( )
A.1 B.2 C.3 D.4
【关键点拨】
变式练4:如图,边长为1的两个正方形互相重合,其中一个不动,另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是 ( )
A.-1 B.+1
C. D.
任务四 在平面直角坐标系中根据旋转求坐标
母题5 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O旋转150°得到△OA'B',则点A'的坐标为 .
【关键点拨】
变式练5:将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点旋转120°得到△OA'B',则点A的对应点A'的坐标为 .
任务五 利用旋转解决以特殊图形为背景的题目
子任务1 以特殊三角形为背景的旋转问题
母题6 如图,等边三角形ABC内有一点O,已知OA=4,OB=3,OC=5,求∠AOB的度数.
【关键点拨】
给什么,得什么 由线段OA,OB,OC的长度,可知它们是一组勾股数,可构造直角三角形
求什么,想什么 求∠AOB的度数,但由线段OA,OB,OC的长度无法直接求出,考虑利用旋转 将已知的三条线段移到同一个三角形中,可考虑旋转△BOC
变式练6:如图,在等腰三角形ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,且DA=1,DC=2,DB=3.
(1)若△ACD绕点C按顺时针方向旋转90°后所得的三角形为△BCE,请作出△BCE.
(2)连接DE,判断△BDE的形状.
(3)求∠ADC的度数.
子任务2 以正方形为背景的旋转问题
母题7 如图,P为正方形ABCD的边CD上一点,∠BAP的平分线交BC于点Q,求证:AP=DP+BQ.
【关键点拨】
给什么,得什么 由正方形ABCD的性质,得四条边相等,四个角都是直角;由AQ平分∠PAB,得∠PAQ=∠BAQ
求什么,想什么 求证AP=DP+BQ,考虑如何把线段DP,BQ转移到同一条直线上,因为AP,DP在△ADP中,BQ在△ABQ中,所以考虑将△ABQ绕点A逆时针旋转90°, 得到△ADE,则ED=BQ
差什么,找什么 需证PE=AP,由旋转的性质和角平分线的性质可得∠E=∠PAE
变式练7:如图,正方形ABCD的边长是5,点E在DC上,将△ADE顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度.
(2)如果连接EF,那么△AEF是怎样的三角形 请说明理由.
(3)△ABF向右平移到△DCH的位置,平移的距离是多少
(4)试猜想线段AE与DH的数量关系和位置关系,并说明理由.
参考答案
母题1 D 提示:∵∠BAC=90°,∠B=60°,
∴BC=2AB=2.
∵Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,
∴AD=AB.
∵∠B=60°,
∴△ABD为等边三角形,
∴BD=AB=1,
∴CD=BC-BD=2-1=1.
故选D.
变式练1 75° 提示:∵在Rt△ABC中,∠ACB=90°,∠B=60°,CD⊥AB,
∴∠BCD=30°.
∵△ACB绕点C逆时针旋转到△ECD的位置,
∴∠ECA=∠BCD=30°,CE=AC,
∴△ACE是等腰三角形,
∴∠CAE=×(180°-30°)=75°.
故答案为75°.
母题2 解:如图,四边形EFGH为所作.
变式练2 解:如图,△ADE为所求.
母题3 解:(1)如图,△A1B1C1为所求,B1,C1两点的坐标分别为(3,3),(7,3).
(2)如图,△A1 B2C2为所求,B2,C2两点的坐标分别为(6,4),(6,8).
变式练3 解:(1)如图,△A1OB1为所作.
(2)A1(0,1),B1(-2,2).
(3)线段AB1的长度==.
母题4 A 提示:如图,设AB与OE交于点N,BC与OG交于点M,
∵四边形ABCD和四边形EFGO都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠EOG=90°,
∴∠BON=∠COM.
在△OBN和△OCM中,
∴△OBN≌△OCM(ASA),
∴S△OBN=S△OCM,
∴S四边形OMBN=S△OBC=S正方形ABCD=×2×2=1.
故选A.
变式练4 A 提示:如图,连接AE.
∵四边形ABCD为正方形,
∴AB=BC=1,且∠B=90°.
由旋转易得∠D'CE=45°,
由勾股定理得AC==.
由题意得AD'=AB=1,∠AD'E=90°,
∴D'C=-1,∠D'EC=∠D'CE=45°,
∴D'E=D'C=-1,
∴S△D'EC=×(-1)2=-,
∴S阴影=×1×1-=-1.
故选A.
母题5 (0,-4)或(-2,-2)
提示:∵∠ABO=90°,∠A=30°,
∴∠AOB=60°.
①若是顺时针旋150°,如图1,点A'在y轴负半轴上,
则OA'=OA=4,
∴点A'的坐标为(0,-4).
②若是逆时针旋转150°,如图2,
∵旋转角为150°,
∴OA'与x轴负半轴夹角为30°.
过点A'作A'C⊥x轴于点C,
则A'C=OA'=×4=2,
由勾股定理得OC===2,
∴点A'的坐标为(-2,-2).
综上所述,点A'的坐标为(0,-4)或(-2,-2).
故答案为(0,-4)或(-2,-2).
变式练5 (-3,)或(0,-2) 提示:由题意可知∠AOB=30°,
∴点A的纵坐标为OA=×2=,
∴点A的横坐标为=3,
∴点A的坐标为(3,).
①当三角板绕原点逆时针旋转120°时,如图1所示:
可知点A'与点A关于y轴对称,
∴点A'的坐标为(-3,).
②当三角板绕原点顺时针旋转120°时,如图2所示:
∵OA=2,
∴点A'的坐标为(0,-2).
综上所述,点A'的坐标为(-3,)或(0,-2).
故答案为 (-3,)或(0,-2).
母题6 解:∵△ABC为等边三角形,
∴BA=BC.
可将△BOC绕点B逆时针旋转60°得△BEA,连接EO,如图,
则BE=BO=3,AE=CO=5,∠OBE=60°,
∴△BOE为等边三角形,
∴OE=OB=3,∠BOE=60°.
∵在△AEO中,AE=5,AO=4,OE=3,
∴AE2=OE2+OA2,
∴△AOE为直角三角形,且∠AOE=90°,
∴∠AOB=90°+60°=150°.
变式练6 解:(1)如图,△BCE为所作.
(2)∵△ACD绕点C按顺时针方向旋转90°后所得的三角形为△BCE,
∴∠DCE=∠ACB=90°,BE=AD=1,CE=CD=2,
∴△DCE为等腰直角三角形,
∴DE=CD=2.
在△BDE中,∵DE=2,BE=1,BD=3,
∴DE2+BE2=BD2,
∴△BDE为直角三角形,∠BED=90°.
(3)∵△DCE为等腰直角三角形,
∴∠DEC=45°,
∴∠BEC=∠BED+∠DEC=90°+45°=135°.
∵△ACD绕点C按顺时针方向旋转90°后所得的三角形为△BCE,
∴∠ADC=∠BEC=135°.
母题7 证明:如图,将△ABQ绕点A逆时针旋转90°得到△ADE,
由旋转的性质可得出∠E=∠AQB,∠EAD=∠QAB,DE=BQ.
又∵∠PAE=90°-∠PAQ=90°-∠BAQ=∠DAQ=∠AQB=∠E,
∴AP=PE=DP+DE=DP+BQ.
变式练7 解:(1)旋转的中心是点A,旋转的角度是90°.
(2)△AEF是等腰直角三角形.
理由:∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)∵正方形ABCD的边长是5,
∴△ABF向右平移到△DCH的位置,平移的距离是5.
(4)AE=DH,AE⊥DH.
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF.
又∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
任务一 求旋转图形中相关角度的大小或线段的长度
母题1 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,∠BAC=90°,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为 ( )
A.0.5 B.1.5 C. D.1
【关键点拨】
变式练1:如图,在Rt△ACB中,∠ACB=90°,∠B=60°,将△ACB绕点C逆时针旋转到△ECD的位置,当CD⊥AB时,连接AE,则∠CAE的度数为 .
任务二 旋转作图
子任务1 已知旋转中心和一对对应点,求作旋转后的图形
母题2 如图,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定点B,C,D的对应点的位置以及旋转后的四边形.
变式练2:如图,在Rt△ABC中,∠B=90°,将△ABC绕点A顺时针旋转得到△ADE,点B,C的对应点分别为点D,E,点D落在AC边上.尺规作图:作出△ADE(不写作法,保留作图痕迹).
子任务2 平面直角坐标系中的旋转作图
母题3 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1).
(1)把△ABC平移后,其中点A平移到点A1(4,5),在图中画出平移后得到的△A1B1C1,并写出点B1,C1的坐标.
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在图中画出旋转后的△A1B2C2,并写出点B2,C2的坐标.
变式练3:如图,在平面直角坐标系中,△AOB的三个顶点坐标分别为A(1,0),O(0,0),B(2,2).以点O为旋转中心,将△AOB逆时针旋转90°,得到△A1OB1.
(1)画出△A1OB1.
(2)直接写出点A1和点B1的坐标.
(3)求线段AB1的长度.
任务三 利用旋转的性质求阴影部分的面积
母题4 如图,正方形ABCD和正方形EFGO的边长都是2,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积是 ( )
A.1 B.2 C.3 D.4
【关键点拨】
变式练4:如图,边长为1的两个正方形互相重合,其中一个不动,另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是 ( )
A.-1 B.+1
C. D.
任务四 在平面直角坐标系中根据旋转求坐标
母题5 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O旋转150°得到△OA'B',则点A'的坐标为 .
【关键点拨】
变式练5:将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点旋转120°得到△OA'B',则点A的对应点A'的坐标为 .
任务五 利用旋转解决以特殊图形为背景的题目
子任务1 以特殊三角形为背景的旋转问题
母题6 如图,等边三角形ABC内有一点O,已知OA=4,OB=3,OC=5,求∠AOB的度数.
【关键点拨】
给什么,得什么 由线段OA,OB,OC的长度,可知它们是一组勾股数,可构造直角三角形
求什么,想什么 求∠AOB的度数,但由线段OA,OB,OC的长度无法直接求出,考虑利用旋转 将已知的三条线段移到同一个三角形中,可考虑旋转△BOC
变式练6:如图,在等腰三角形ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,且DA=1,DC=2,DB=3.
(1)若△ACD绕点C按顺时针方向旋转90°后所得的三角形为△BCE,请作出△BCE.
(2)连接DE,判断△BDE的形状.
(3)求∠ADC的度数.
子任务2 以正方形为背景的旋转问题
母题7 如图,P为正方形ABCD的边CD上一点,∠BAP的平分线交BC于点Q,求证:AP=DP+BQ.
【关键点拨】
给什么,得什么 由正方形ABCD的性质,得四条边相等,四个角都是直角;由AQ平分∠PAB,得∠PAQ=∠BAQ
求什么,想什么 求证AP=DP+BQ,考虑如何把线段DP,BQ转移到同一条直线上,因为AP,DP在△ADP中,BQ在△ABQ中,所以考虑将△ABQ绕点A逆时针旋转90°, 得到△ADE,则ED=BQ
差什么,找什么 需证PE=AP,由旋转的性质和角平分线的性质可得∠E=∠PAE
变式练7:如图,正方形ABCD的边长是5,点E在DC上,将△ADE顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度.
(2)如果连接EF,那么△AEF是怎样的三角形 请说明理由.
(3)△ABF向右平移到△DCH的位置,平移的距离是多少
(4)试猜想线段AE与DH的数量关系和位置关系,并说明理由.
参考答案
母题1 D 提示:∵∠BAC=90°,∠B=60°,
∴BC=2AB=2.
∵Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,
∴AD=AB.
∵∠B=60°,
∴△ABD为等边三角形,
∴BD=AB=1,
∴CD=BC-BD=2-1=1.
故选D.
变式练1 75° 提示:∵在Rt△ABC中,∠ACB=90°,∠B=60°,CD⊥AB,
∴∠BCD=30°.
∵△ACB绕点C逆时针旋转到△ECD的位置,
∴∠ECA=∠BCD=30°,CE=AC,
∴△ACE是等腰三角形,
∴∠CAE=×(180°-30°)=75°.
故答案为75°.
母题2 解:如图,四边形EFGH为所作.
变式练2 解:如图,△ADE为所求.
母题3 解:(1)如图,△A1B1C1为所求,B1,C1两点的坐标分别为(3,3),(7,3).
(2)如图,△A1 B2C2为所求,B2,C2两点的坐标分别为(6,4),(6,8).
变式练3 解:(1)如图,△A1OB1为所作.
(2)A1(0,1),B1(-2,2).
(3)线段AB1的长度==.
母题4 A 提示:如图,设AB与OE交于点N,BC与OG交于点M,
∵四边形ABCD和四边形EFGO都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠EOG=90°,
∴∠BON=∠COM.
在△OBN和△OCM中,
∴△OBN≌△OCM(ASA),
∴S△OBN=S△OCM,
∴S四边形OMBN=S△OBC=S正方形ABCD=×2×2=1.
故选A.
变式练4 A 提示:如图,连接AE.
∵四边形ABCD为正方形,
∴AB=BC=1,且∠B=90°.
由旋转易得∠D'CE=45°,
由勾股定理得AC==.
由题意得AD'=AB=1,∠AD'E=90°,
∴D'C=-1,∠D'EC=∠D'CE=45°,
∴D'E=D'C=-1,
∴S△D'EC=×(-1)2=-,
∴S阴影=×1×1-=-1.
故选A.
母题5 (0,-4)或(-2,-2)
提示:∵∠ABO=90°,∠A=30°,
∴∠AOB=60°.
①若是顺时针旋150°,如图1,点A'在y轴负半轴上,
则OA'=OA=4,
∴点A'的坐标为(0,-4).
②若是逆时针旋转150°,如图2,
∵旋转角为150°,
∴OA'与x轴负半轴夹角为30°.
过点A'作A'C⊥x轴于点C,
则A'C=OA'=×4=2,
由勾股定理得OC===2,
∴点A'的坐标为(-2,-2).
综上所述,点A'的坐标为(0,-4)或(-2,-2).
故答案为(0,-4)或(-2,-2).
变式练5 (-3,)或(0,-2) 提示:由题意可知∠AOB=30°,
∴点A的纵坐标为OA=×2=,
∴点A的横坐标为=3,
∴点A的坐标为(3,).
①当三角板绕原点逆时针旋转120°时,如图1所示:
可知点A'与点A关于y轴对称,
∴点A'的坐标为(-3,).
②当三角板绕原点顺时针旋转120°时,如图2所示:
∵OA=2,
∴点A'的坐标为(0,-2).
综上所述,点A'的坐标为(-3,)或(0,-2).
故答案为 (-3,)或(0,-2).
母题6 解:∵△ABC为等边三角形,
∴BA=BC.
可将△BOC绕点B逆时针旋转60°得△BEA,连接EO,如图,
则BE=BO=3,AE=CO=5,∠OBE=60°,
∴△BOE为等边三角形,
∴OE=OB=3,∠BOE=60°.
∵在△AEO中,AE=5,AO=4,OE=3,
∴AE2=OE2+OA2,
∴△AOE为直角三角形,且∠AOE=90°,
∴∠AOB=90°+60°=150°.
变式练6 解:(1)如图,△BCE为所作.
(2)∵△ACD绕点C按顺时针方向旋转90°后所得的三角形为△BCE,
∴∠DCE=∠ACB=90°,BE=AD=1,CE=CD=2,
∴△DCE为等腰直角三角形,
∴DE=CD=2.
在△BDE中,∵DE=2,BE=1,BD=3,
∴DE2+BE2=BD2,
∴△BDE为直角三角形,∠BED=90°.
(3)∵△DCE为等腰直角三角形,
∴∠DEC=45°,
∴∠BEC=∠BED+∠DEC=90°+45°=135°.
∵△ACD绕点C按顺时针方向旋转90°后所得的三角形为△BCE,
∴∠ADC=∠BEC=135°.
母题7 证明:如图,将△ABQ绕点A逆时针旋转90°得到△ADE,
由旋转的性质可得出∠E=∠AQB,∠EAD=∠QAB,DE=BQ.
又∵∠PAE=90°-∠PAQ=90°-∠BAQ=∠DAQ=∠AQB=∠E,
∴AP=PE=DP+DE=DP+BQ.
变式练7 解:(1)旋转的中心是点A,旋转的角度是90°.
(2)△AEF是等腰直角三角形.
理由:∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)∵正方形ABCD的边长是5,
∴△ABF向右平移到△DCH的位置,平移的距离是5.
(4)AE=DH,AE⊥DH.
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF.
又∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
同课章节目录
