24.3 正多边形和圆 同步培优训练 (含答案)2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 24.3 正多边形和圆 同步培优训练 (含答案)2024-2025学年数学人教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 265.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:17:02 | ||
图片预览

文档简介
24.3 正多边形和圆
任务一 正多边形与圆的有关计算
母题1 若一个正三角形和一个正六边形的面积相等,则正三角形与正六边形的边长比为 ( )
A.∶1 B.1∶
C.∶1 D.2∶1
变式练1:同一个圆的内接正方形和正三角形的边心距的比为 .
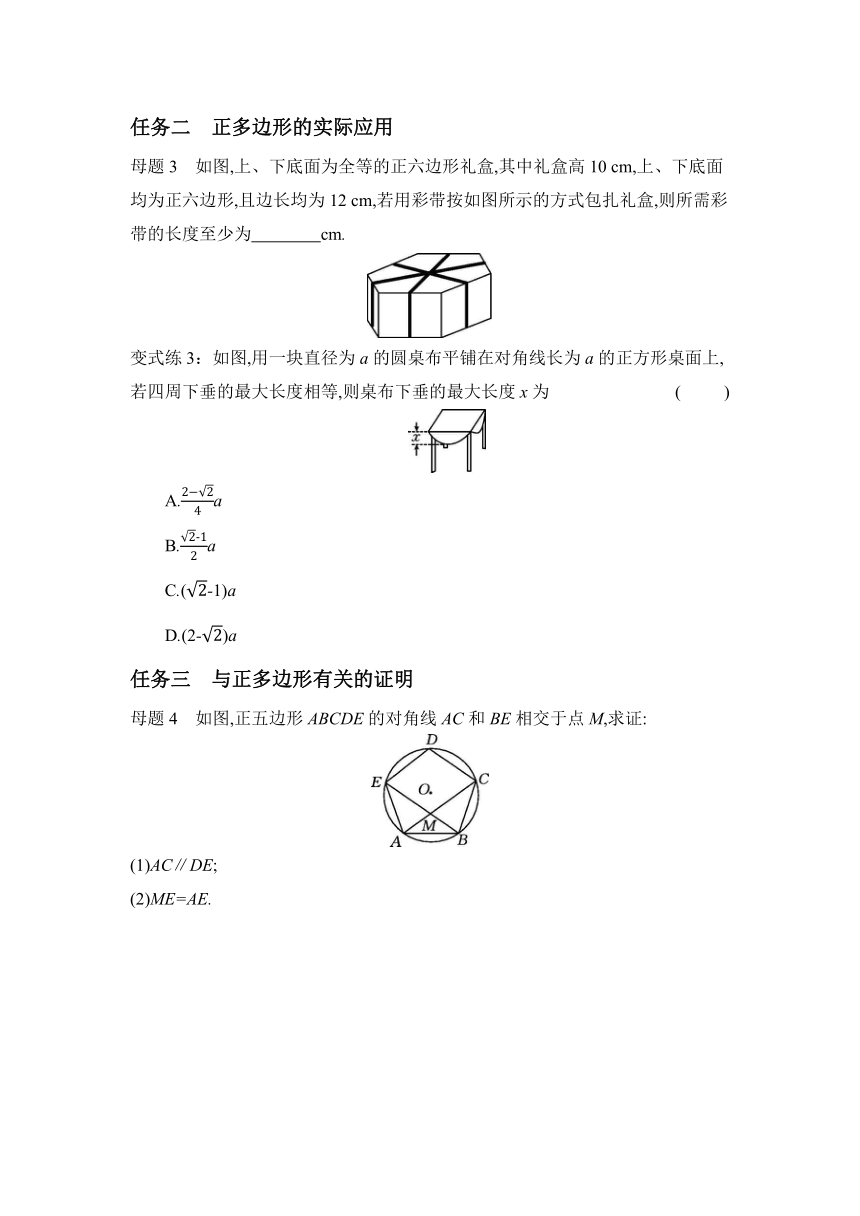
母题2 如图,正六边形ABCDEF内接于☉O,连接AD,已知☉O的周长等于6π cm.
(1)求∠ADB的度数.
(2)求正六边形ABCDEF的周长和面积.
变式练2:如图,☉O的周长等于8π cm,正六边形ABCDEF内接于☉O.
(1)求圆心O到CD的距离.
(2)求正六边形ABCDEF的面积.
任务二 正多边形的实际应用
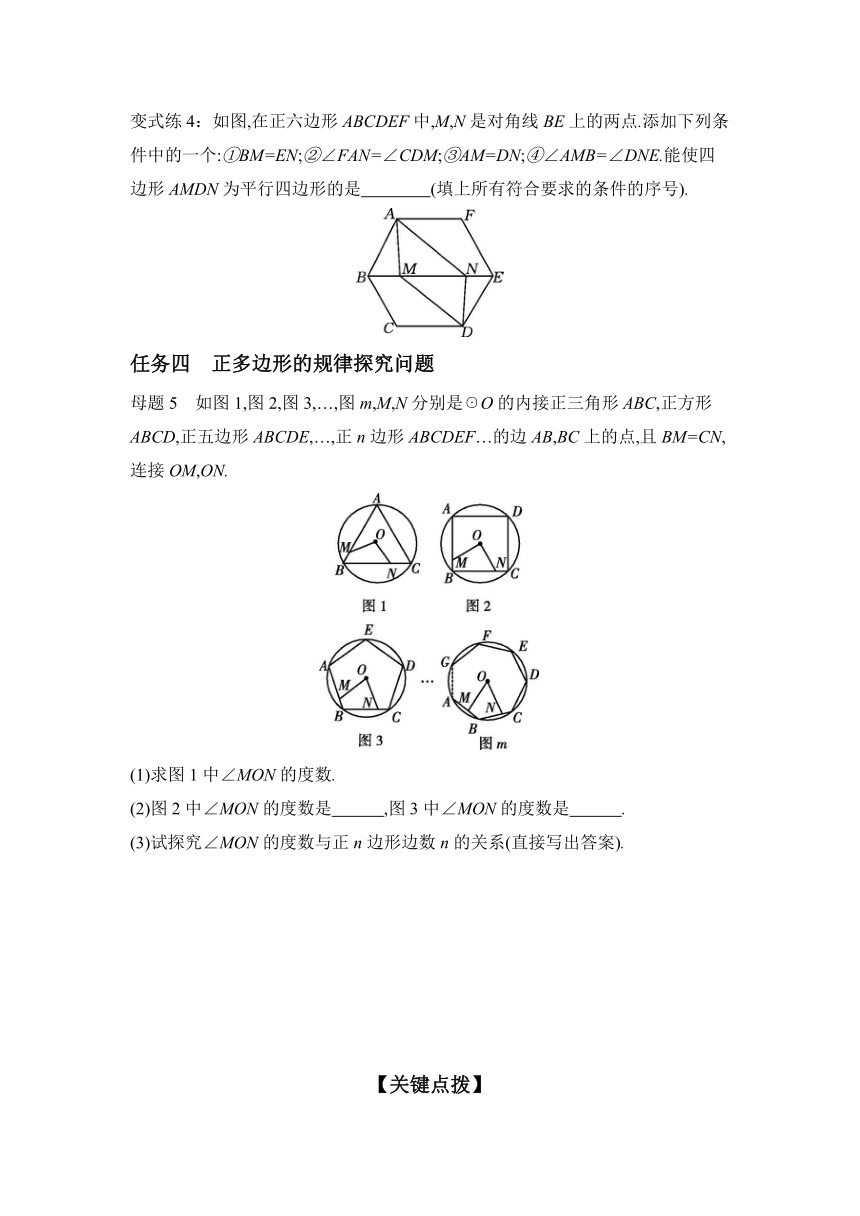
母题3 如图,上、下底面为全等的正六边形礼盒,其中礼盒高10 cm,上、下底面均为正六边形,且边长均为12 cm,若用彩带按如图所示的方式包扎礼盒,则所需彩带的长度至少为 cm.
变式练3:如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为 ( )
A.a
B.a
C.(-1)a
D.(2-)a
任务三 与正多边形有关的证明
母题4 如图,正五边形ABCDE的对角线AC和BE相交于点M,求证:
(1)AC∥DE;
(2)ME=AE.
变式练4:如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠FAN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN为平行四边形的是 (填上所有符合要求的条件的序号).
任务四 正多边形的规律探究问题
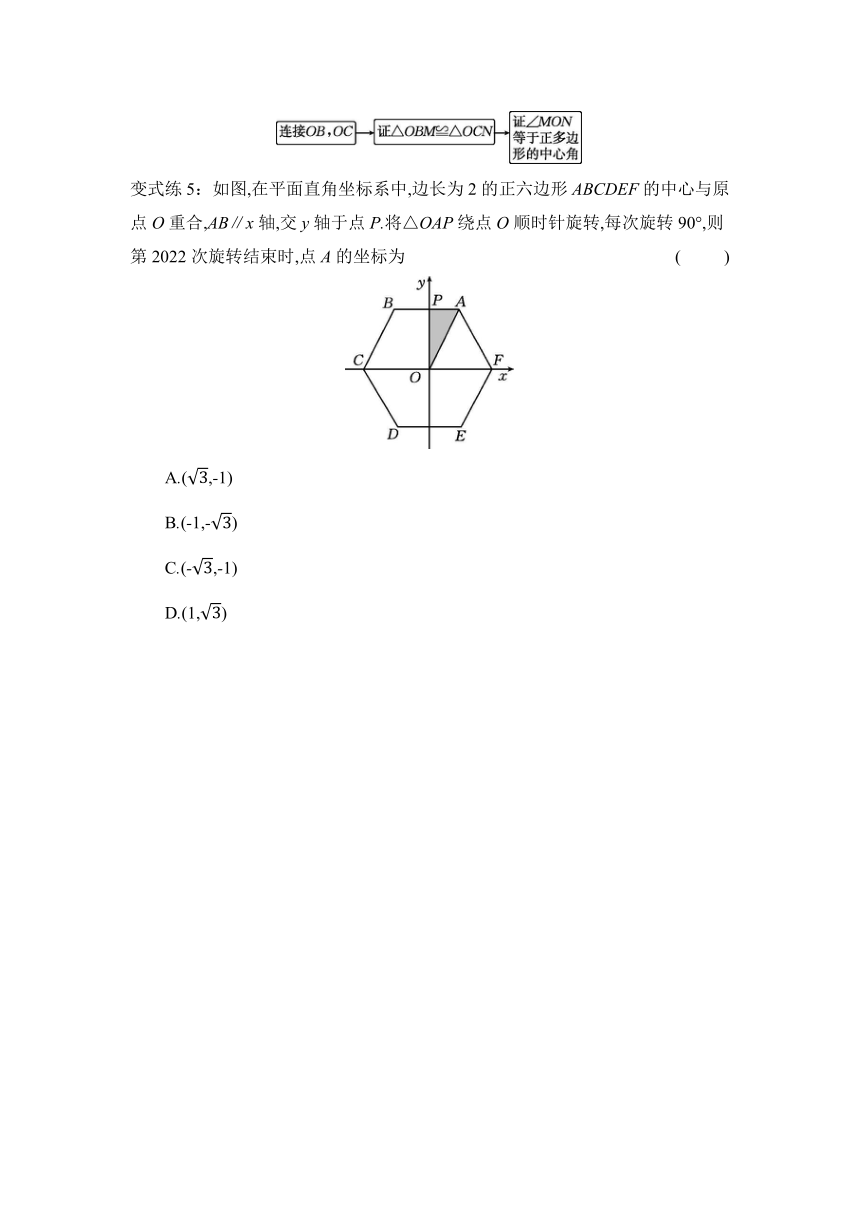
母题5 如图1,图2,图3,…,图m,M,N分别是☉O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图1中∠MON的度数.
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
【关键点拨】
变式练5:如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点A的坐标为 ( )
A.(,-1)
B.(-1,-)
C.(-,-1)
D.(1,)
参考答案
母题1 A 提示:设正三角形和正六边形的边长分别为a,b,
由题意得 a2=6××b2,
∴a=b,
∴a∶b=∶1,
故选A.
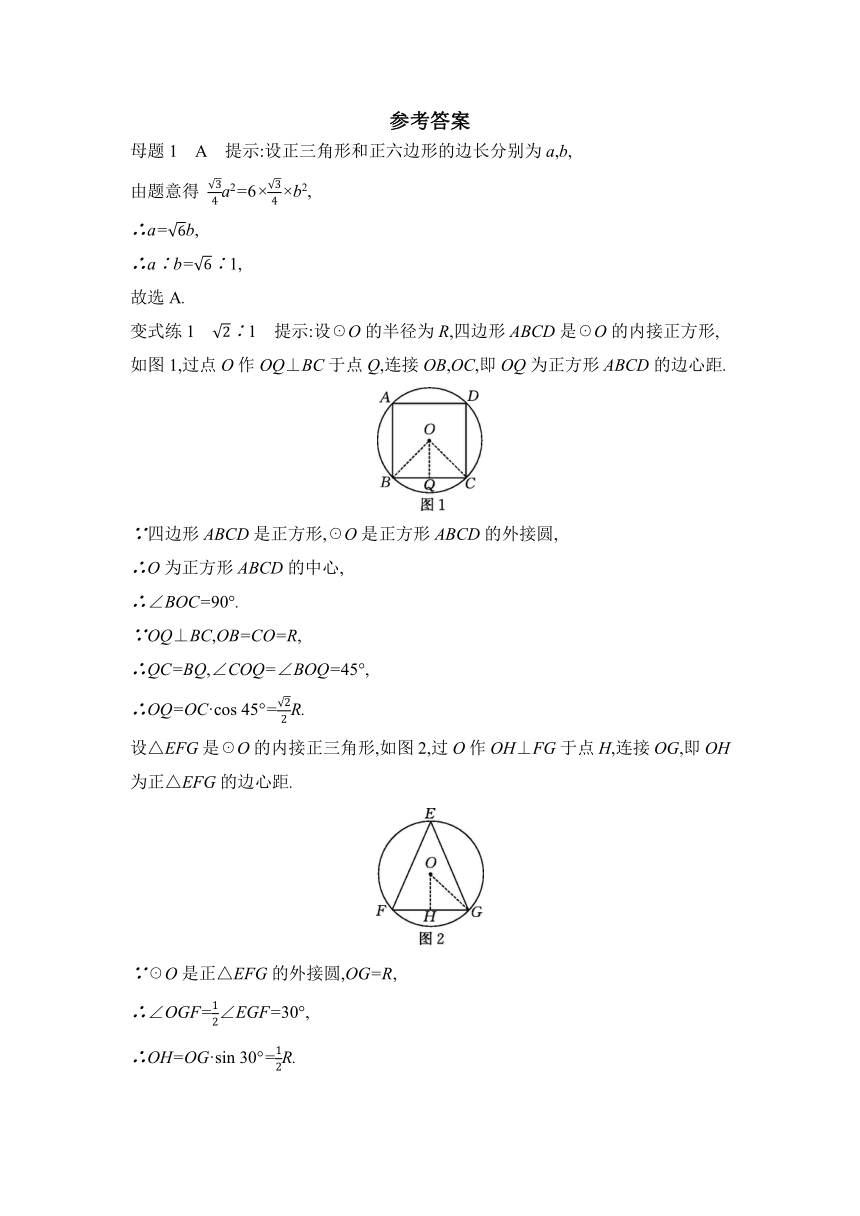
变式练1 ∶1 提示:设☉O的半径为R,四边形ABCD是☉O的内接正方形,如图1,过点O作OQ⊥BC于点Q,连接OB,OC,即OQ为正方形ABCD的边心距.
∵四边形ABCD是正方形,☉O是正方形ABCD的外接圆,
∴O为正方形ABCD的中心,
∴∠BOC=90°.
∵OQ⊥BC,OB=CO=R,
∴QC=BQ,∠COQ=∠BOQ=45°,
∴OQ=OC·cos 45°=R.
设△EFG是☉O的内接正三角形,如图2,过O作OH⊥FG于点H,连接OG,即OH为正△EFG的边心距.
∵☉O是正△EFG的外接圆,OG=R,
∴∠OGF=∠EGF=30°,
∴OH=OG·sin 30°=R.
∴OQ∶OH=∶=∶1.
故答案为 ∶1.
母题2 解:(1)如图,连接OB.
∵正六边形ABCDEF内接于☉O,
∴∠AOB=×360°=60°,
∴∠ADB=30°.
(2)如图,过点O作OH⊥AB于点H,
∴AH=AB.
∵☉O的周长等于6π cm,
∴☉O的半径为3 cm.
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA=3 cm,∴AH= cm,
∴OH==(cm),
∴S正六边形ABCDEF=6S△OAB=6××3×=(cm2),
C正六边形ABCDEF=6×3=18(cm),
∴正六边形ABCDEF的周长为18 cm,面积为 cm2.
变式练2 解:(1)如图,连接OC,OD,过点O作OH⊥CD于点H.
∵☉O的周长等于8π cm,∴半径OC=4 cm.
∵六边形ABCDEF是正六边形,
∴∠COD=60°,∴∠COH=30°,∴CH=OC=2 cm.
∵OH2+CH2=OC2,∴OH2+22=42,解得OH=2 cm,
∴圆心O到CD的距离为2 cm.
(2)正六边形ABCDEF的面积为×4×2×6=24(cm2).
母题3 72+60 提示:根据题意,作出实际图形的上底,如图,AC,CD是上底面的两边,作CB⊥AD于点B.
∵∠ACD=120°,AC=12 cm,
∴∠ACB=×120°=60°,
∴AB=AC·sin 60°=12×=6 cm,
∴AD=12 cm.
∵礼盒高10 cm,
∴彩带的长至少=12×6+10×6=(72+60)cm.
故答案为72+60.
变式练3 A 提示:如图,正方形ABCD为直径为a的☉O的内接正方形,作OE⊥BC于点E,交☉O于点F,连接OB,则OB=a,
∴△OBE为等腰直角三角形,
∴OE=OB=a,
∴EF=OF-OE=a-a=a,
即桌布下垂的最大长度x为a.
故选A.
母题4 证明:(1)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AB=BC,
∴∠CAB=∠BCA=36°,
∴∠EAC=108°-36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴AC∥DE.
(2)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AE=AB,
∴∠AEB=∠ABE=36°.
∵∠EAC=72°,
∴∠EMA=180°-36°-72°=72°,
∴∠EAM=∠EMA,
∴ME=AE.
变式练4 ①②④ 提示:①连接AD,交BE于点O,
∵正六边形ABCDEF中,∠BAO=∠ABO=∠OED=∠ODE=60°,
∴等边△AOB和等边△DOE全等,
∴OA=OD,OB=OE,
又∵BM=EN,
∴OM=ON,
∴四边形AMDN是平行四边形,故①符合题意;
②∵∠FAN=∠CDM,∠CDA=∠DAF,
∴∠OAN=∠ODM,
∴AN∥DM,
又∵∠AON=∠DOM,OA=OD,
∴△AON≌△DOM(ASA),
∴AN=DM,
∴四边形AMDN是平行四边形,故②符合题意;
③∵AM=DN,AB=DE,∠ABM=∠DEN,
∴△ABM与△DEN不一定全等,不能得出四边形AMDN是平行四边形,故③不符合题意;
④∵∠AMB=∠DNE,∠ABM=∠DEN,AB=DE,
∴△ABM≌△DEN(AAS),
∴AM=DN,
∵∠AMB+∠AMN=180°,∠DNM+∠DNE=180°,
∴∠AMN=∠DNM,
∴AM∥DN,
∴四边形AMDN是平行四边形,故④符合题意.
故答案为①②④.
母题5 解:(1)如图,连接OC,OB.
∵正三角形ABC内接于☉O,
∴OB=OC,∠BOC=120°,∠OBM=∠OCN=∠OBC=30°.
∵BM=CN,
∴△BOM≌△CON(SAS),
∴∠BOM=∠CON,
∴∠CON+∠BON=∠BON+∠BOM,
∴∠MON=∠BOC=120°.
(2)90°;72°.
(3)∠MON=.
变式练5 B 提示:∵边长为2的正六边形ABCDEF的中心与原点O重合,
∴OA=AB=2,∠BAO=60°.
∵AB∥x轴,
∴∠APO=90°,
∴∠AOP=30°,
∴AP=1,OP=,
∴A(1, ),
∵将△OAP绕点O顺时针旋转,每次旋转90°,可知点A2与点D重合,
由360°÷90°=4可知,每4次为一个循环,
∵2022÷4=505……2,
∴点A2022与点A2重合.
∵点A2与点A关于原点O对称,
∴A2(-1,-),
∴第2022次旋转结束时,点A的坐标为(-1,-),
故选B.
任务一 正多边形与圆的有关计算
母题1 若一个正三角形和一个正六边形的面积相等,则正三角形与正六边形的边长比为 ( )
A.∶1 B.1∶
C.∶1 D.2∶1
变式练1:同一个圆的内接正方形和正三角形的边心距的比为 .
母题2 如图,正六边形ABCDEF内接于☉O,连接AD,已知☉O的周长等于6π cm.
(1)求∠ADB的度数.
(2)求正六边形ABCDEF的周长和面积.
变式练2:如图,☉O的周长等于8π cm,正六边形ABCDEF内接于☉O.
(1)求圆心O到CD的距离.
(2)求正六边形ABCDEF的面积.
任务二 正多边形的实际应用
母题3 如图,上、下底面为全等的正六边形礼盒,其中礼盒高10 cm,上、下底面均为正六边形,且边长均为12 cm,若用彩带按如图所示的方式包扎礼盒,则所需彩带的长度至少为 cm.
变式练3:如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为 ( )
A.a
B.a
C.(-1)a
D.(2-)a
任务三 与正多边形有关的证明
母题4 如图,正五边形ABCDE的对角线AC和BE相交于点M,求证:
(1)AC∥DE;
(2)ME=AE.
变式练4:如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠FAN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN为平行四边形的是 (填上所有符合要求的条件的序号).
任务四 正多边形的规律探究问题
母题5 如图1,图2,图3,…,图m,M,N分别是☉O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图1中∠MON的度数.
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
【关键点拨】
变式练5:如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点A的坐标为 ( )
A.(,-1)
B.(-1,-)
C.(-,-1)
D.(1,)
参考答案
母题1 A 提示:设正三角形和正六边形的边长分别为a,b,
由题意得 a2=6××b2,
∴a=b,
∴a∶b=∶1,
故选A.
变式练1 ∶1 提示:设☉O的半径为R,四边形ABCD是☉O的内接正方形,如图1,过点O作OQ⊥BC于点Q,连接OB,OC,即OQ为正方形ABCD的边心距.
∵四边形ABCD是正方形,☉O是正方形ABCD的外接圆,
∴O为正方形ABCD的中心,
∴∠BOC=90°.
∵OQ⊥BC,OB=CO=R,
∴QC=BQ,∠COQ=∠BOQ=45°,
∴OQ=OC·cos 45°=R.
设△EFG是☉O的内接正三角形,如图2,过O作OH⊥FG于点H,连接OG,即OH为正△EFG的边心距.
∵☉O是正△EFG的外接圆,OG=R,
∴∠OGF=∠EGF=30°,
∴OH=OG·sin 30°=R.
∴OQ∶OH=∶=∶1.
故答案为 ∶1.
母题2 解:(1)如图,连接OB.
∵正六边形ABCDEF内接于☉O,
∴∠AOB=×360°=60°,
∴∠ADB=30°.
(2)如图,过点O作OH⊥AB于点H,
∴AH=AB.
∵☉O的周长等于6π cm,
∴☉O的半径为3 cm.
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA=3 cm,∴AH= cm,
∴OH==(cm),
∴S正六边形ABCDEF=6S△OAB=6××3×=(cm2),
C正六边形ABCDEF=6×3=18(cm),
∴正六边形ABCDEF的周长为18 cm,面积为 cm2.
变式练2 解:(1)如图,连接OC,OD,过点O作OH⊥CD于点H.
∵☉O的周长等于8π cm,∴半径OC=4 cm.
∵六边形ABCDEF是正六边形,
∴∠COD=60°,∴∠COH=30°,∴CH=OC=2 cm.
∵OH2+CH2=OC2,∴OH2+22=42,解得OH=2 cm,
∴圆心O到CD的距离为2 cm.
(2)正六边形ABCDEF的面积为×4×2×6=24(cm2).
母题3 72+60 提示:根据题意,作出实际图形的上底,如图,AC,CD是上底面的两边,作CB⊥AD于点B.
∵∠ACD=120°,AC=12 cm,
∴∠ACB=×120°=60°,
∴AB=AC·sin 60°=12×=6 cm,
∴AD=12 cm.
∵礼盒高10 cm,
∴彩带的长至少=12×6+10×6=(72+60)cm.
故答案为72+60.
变式练3 A 提示:如图,正方形ABCD为直径为a的☉O的内接正方形,作OE⊥BC于点E,交☉O于点F,连接OB,则OB=a,
∴△OBE为等腰直角三角形,
∴OE=OB=a,
∴EF=OF-OE=a-a=a,
即桌布下垂的最大长度x为a.
故选A.
母题4 证明:(1)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AB=BC,
∴∠CAB=∠BCA=36°,
∴∠EAC=108°-36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴AC∥DE.
(2)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AE=AB,
∴∠AEB=∠ABE=36°.
∵∠EAC=72°,
∴∠EMA=180°-36°-72°=72°,
∴∠EAM=∠EMA,
∴ME=AE.
变式练4 ①②④ 提示:①连接AD,交BE于点O,
∵正六边形ABCDEF中,∠BAO=∠ABO=∠OED=∠ODE=60°,
∴等边△AOB和等边△DOE全等,
∴OA=OD,OB=OE,
又∵BM=EN,
∴OM=ON,
∴四边形AMDN是平行四边形,故①符合题意;
②∵∠FAN=∠CDM,∠CDA=∠DAF,
∴∠OAN=∠ODM,
∴AN∥DM,
又∵∠AON=∠DOM,OA=OD,
∴△AON≌△DOM(ASA),
∴AN=DM,
∴四边形AMDN是平行四边形,故②符合题意;
③∵AM=DN,AB=DE,∠ABM=∠DEN,
∴△ABM与△DEN不一定全等,不能得出四边形AMDN是平行四边形,故③不符合题意;
④∵∠AMB=∠DNE,∠ABM=∠DEN,AB=DE,
∴△ABM≌△DEN(AAS),
∴AM=DN,
∵∠AMB+∠AMN=180°,∠DNM+∠DNE=180°,
∴∠AMN=∠DNM,
∴AM∥DN,
∴四边形AMDN是平行四边形,故④符合题意.
故答案为①②④.
母题5 解:(1)如图,连接OC,OB.
∵正三角形ABC内接于☉O,
∴OB=OC,∠BOC=120°,∠OBM=∠OCN=∠OBC=30°.
∵BM=CN,
∴△BOM≌△CON(SAS),
∴∠BOM=∠CON,
∴∠CON+∠BON=∠BON+∠BOM,
∴∠MON=∠BOC=120°.
(2)90°;72°.
(3)∠MON=.
变式练5 B 提示:∵边长为2的正六边形ABCDEF的中心与原点O重合,
∴OA=AB=2,∠BAO=60°.
∵AB∥x轴,
∴∠APO=90°,
∴∠AOP=30°,
∴AP=1,OP=,
∴A(1, ),
∵将△OAP绕点O顺时针旋转,每次旋转90°,可知点A2与点D重合,
由360°÷90°=4可知,每4次为一个循环,
∵2022÷4=505……2,
∴点A2022与点A2重合.
∵点A2与点A关于原点O对称,
∴A2(-1,-),
∴第2022次旋转结束时,点A的坐标为(-1,-),
故选B.
同课章节目录
