24.4 弧长和扇形面积 同步培优训练(含答案) 2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 24.4 弧长和扇形面积 同步培优训练(含答案) 2024-2025学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 372.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 00:00:00 | ||
图片预览


文档简介
24.4 弧长和扇形面积
任务一 弧长公式的应用
子任务1 弧长公式的实际应用
母题1 图中实线部分是半径为9 m的两条等弧组成的游泳池.若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为 ( )
A.12π m
B.18π m
C.20π m
D.24π m
变式练1:中国高铁的飞速发展,已成为中国式现代化建设的重要标志.如图,这是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.8千米,则这段圆曲线的长为 ( )
A. 千米 B. 千米
C. 千米 D. 千米
子任务2 求图形滚动问题中的路径长
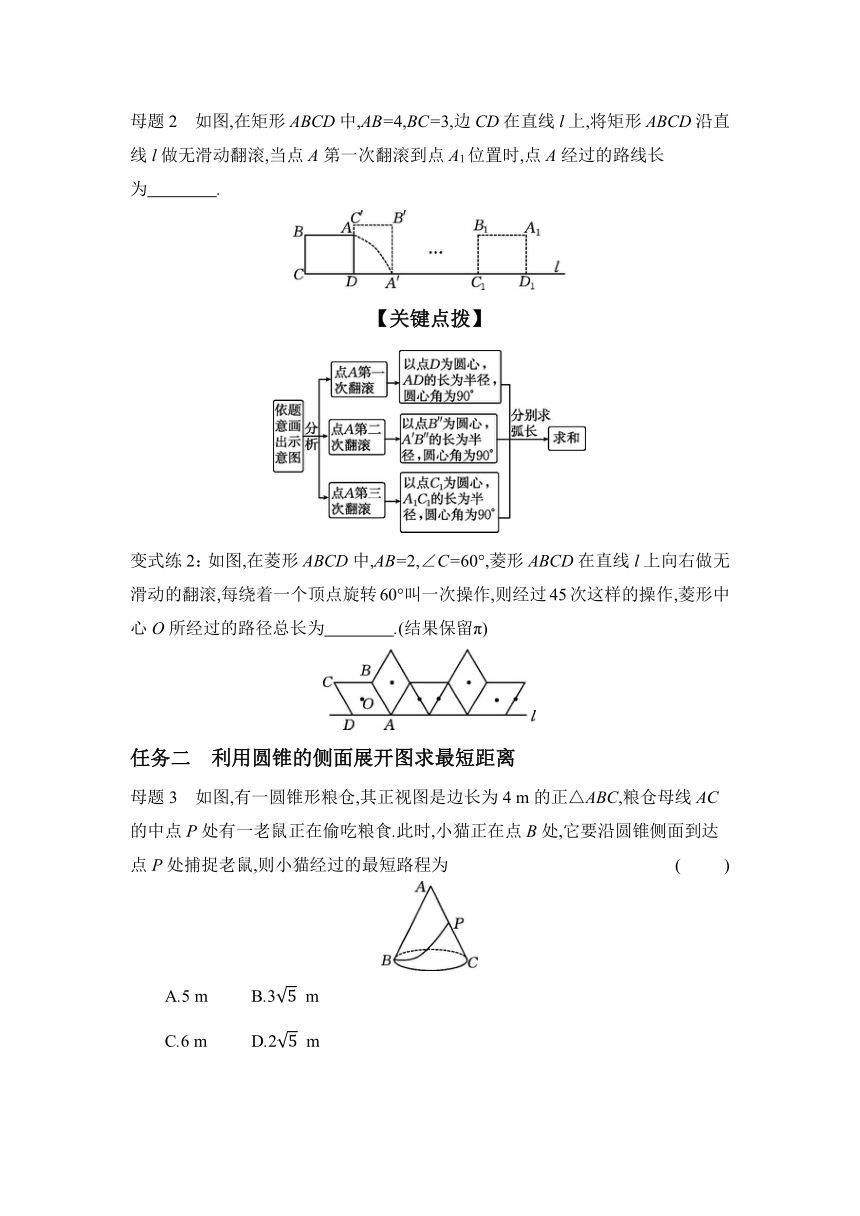
母题2 如图,在矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线l做无滑动翻滚,当点A第一次翻滚到点A1位置时,点A经过的路线长为 .
【关键点拨】
变式练2:如图,在菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右做无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过45次这样的操作,菱形中心O所经过的路径总长为 .(结果保留π)
任务二 利用圆锥的侧面展开图求最短距离
母题3 如图,有一圆锥形粮仓,其正视图是边长为4 m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达
点P处捕捉老鼠,则小猫经过的最短路程为 ( )
A.5 m B.3 m
C.6 m D.2 m
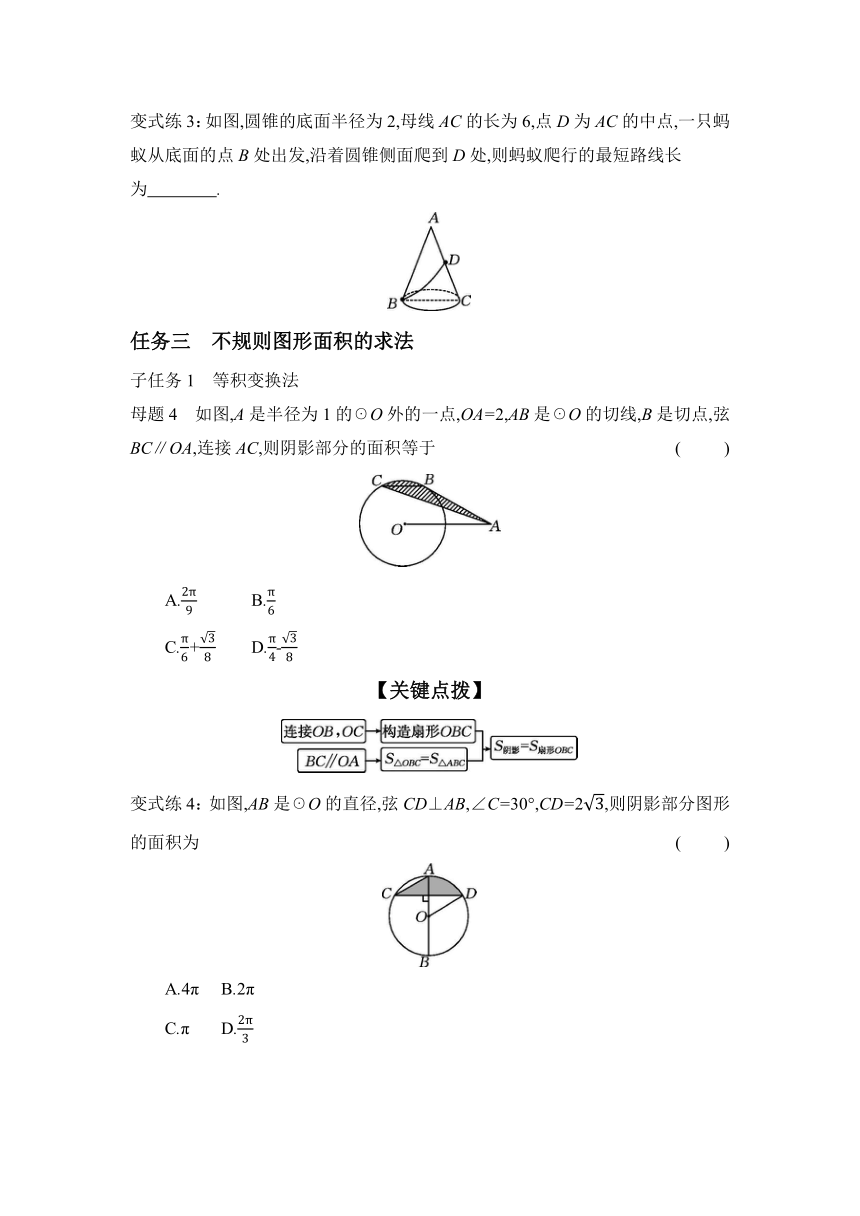
变式练3:如图,圆锥的底面半径为2,母线AC的长为6,点D为AC的中点,一只蚂蚁从底面的点B处出发,沿着圆锥侧面爬到D处,则蚂蚁爬行的最短路线长为 .
任务三 不规则图形面积的求法
子任务1 等积变换法
母题4 如图,A是半径为1的☉O外的一点,OA=2,AB是☉O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于 ( )
A. B.
C.+ D.-
【关键点拨】
变式练4:如图,AB是☉O的直径,弦CD⊥AB,∠C=30°,CD=2,则阴影部分图形的面积为 ( )
A.4π B.2π
C.π D.
子任务2 割补法
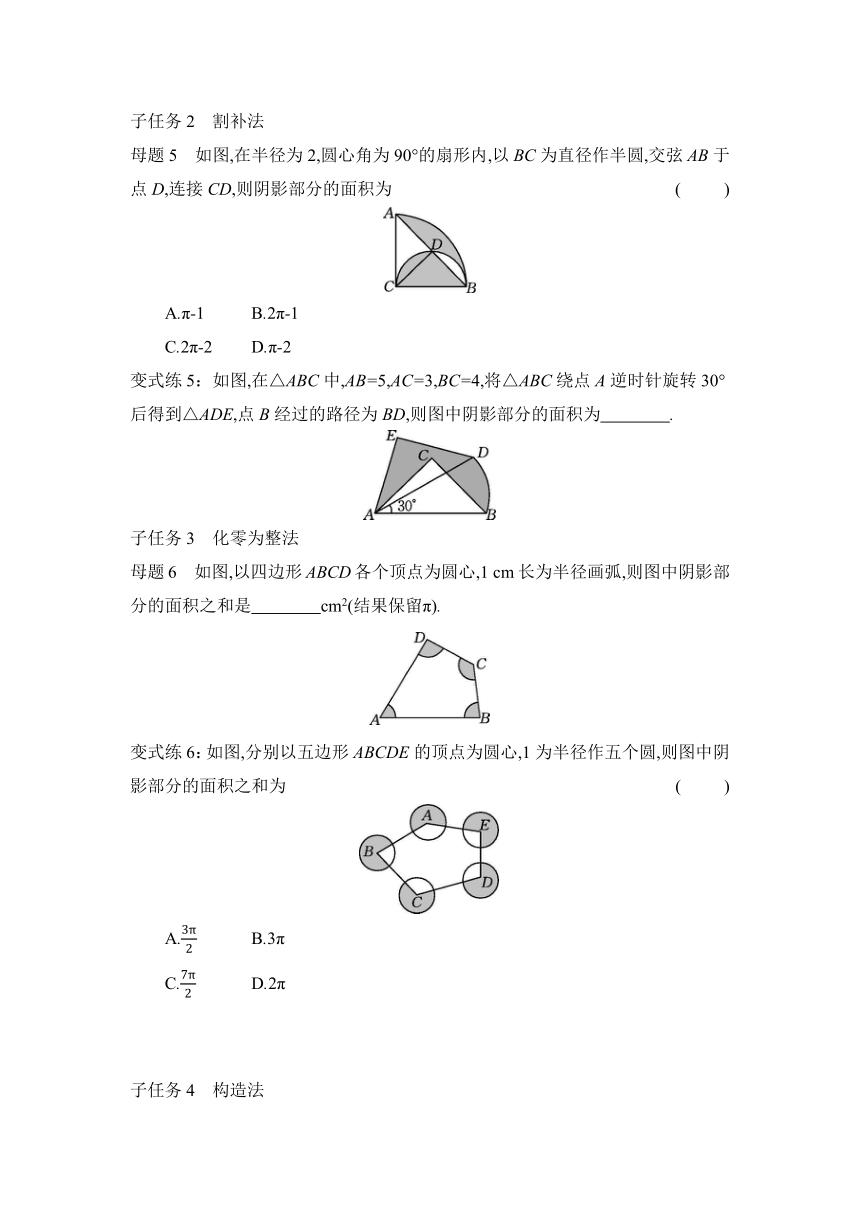
母题5 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为 ( )
A.π-1 B.2π-1
C.2π-2 D.π-2
变式练5:如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为BD,则图中阴影部分的面积为 .
子任务3 化零为整法
母题6 如图,以四边形ABCD各个顶点为圆心,1 cm长为半径画弧,则图中阴影部分的面积之和是 cm2(结果保留π).
变式练6:如图,分别以五边形ABCDE的顶点为圆心,1为半径作五个圆,则图中阴影部分的面积之和为 ( )
A. B.3π
C. D.2π
子任务4 构造法
母题7 如图,正方形ABCD的边长为1,分别以正方形的四个顶点为圆心,边长为半径,在正方形内画圆弧,求图中阴影部分的面积.
变式练7:山西著名工艺品平遥推光漆器外观古朴雅致、闪光发亮,绘饰金碧辉煌,以手掌推出光泽而得名.图1是平遥推光漆器的一种图案,图2是选取其某部分并且放大后的示意图.四边形ABCD是边长为2的正方形,分别以正方形的四个顶点为圆心,对角线的长为半径画弧,四条弧相交于点O,则图中阴影部分的面积为 ( )
A.2π-4 B.π-2
C.2π D. π
任务四 与图形滚动有关的计算
母题8 归纳猜想:同学们,让我们一起进行一次研究性学习.
(1)如图1,已知正三角形ABC的中心为O,半径为R,将其沿直线l向右翻滚,当正三角形翻滚一周时,其中心O经过的路程是多少
图1
(2)如图2,将半径为R的正方形沿直线l向右翻滚,当正方形翻滚一周时,其中心O经过的路程是多少
图2
(3)猜想:如图3,把半径为R的正多边形沿直线l翻滚一周,其中心O所经过的路程是多少 请说明理由.
图3
(4)进一步猜想:当将任意圆的内接多边形沿直线l翻滚一周时,其外心所经过的路程是不是一个定值 为什么 请以任意三角形(如图4)为例说明.
图4
变式练8:如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2的位置,若正六边形的边长为2 cm,求正六边形的中心O运动的路程长.
参考答案
母题1 D
变式练1 C 提示:∵CA,CB是切线,
∴OA⊥AC,OB⊥CB,∴∠OAC=∠OBC=90°,∴∠AOB+∠ACB=180°,∵∠ACB+α=180°,∴∠AOB=α=60°,∴的长==.故选C.
母题2 6π 提示:∵四边形ABCD是矩形,AB=4,BC=3,
∴BC=AD=3,∠ADC=90°,对角线AC=BD=5.
∵根据旋转的性质知,∠ADA'=90°,AD=A'D=BC=3,
∴点A第一次翻滚到点A'位置时,点A经过的路线长为=,
同理,点A'第一次翻滚到点A″位置时,点A'经过的路线长为=2π,
点A″第一次翻滚到点A1位置时,点A″经过的路线长为=,
则当点A第一次翻滚到点A1位置时,点A经过的路线长为+2π+=6π.
故答案为6π.
变式练2 10π+5π 提示:在菱形ABCD中,AB=2,∠C=60°,
所以第一、二次旋转形成弧的半径是,圆心角是60°,
所以第一、二次旋转的弧长和=+=2×=,
因为第三次旋转形成弧的半径是1,圆心角是60°,
所以第三次旋转的弧长==,
因为一个周期为3,
所以45÷3=15,
所以菱形中心O所经过的路径总长为
15×=10π+5π.
故答案为10π+5π.
母题3 D 提示:设圆锥侧面展开图的圆心角为n.
∵圆锥形粮仓的正视图是边长为4 m的正△ABC,
∴圆锥的底面周长是4π,则4π=,
∴n=180°,即圆锥侧面展开图的圆心角是180°.
在圆锥侧面展开图中,AP=2,AB=4,∠BAP=90°.
∴BP===2 m,
故小猫经过的最短距离是2 m.故选D.
变式练3 3 提示:把圆锥沿母线AB展开得到它的侧面积为扇形BAB',C'点为弧BB'的中点,如图,
设∠BAB'=n°,
根据题意得,2π×2=,解得n=120,
∴∠BAC'=60°,
∴△BAC'为等边三角形,
∵点D为AC的中点,
∴点D'为AC'的中点,
∴BD'⊥AC',∴AD'=3,
∴BD'==3,
∴蚂蚁爬行的最短路线长为3.
故答案为3.
母题4 B 提示:如图,连接OB,OC,过点O作OD⊥BC于点D.
∵BC∥OA,
∴点A到BC的距离等于点O到BC的距离,
∴S△BOC=S△ABC,
∴阴影部分的面积=扇形OBC的面积.
∵AB是☉O的切线,
∴OB⊥AB.
∵OA=2,OB=OC=1,
∴∠OAB=30°,
∴∠AOB=60°.
又∵BC∥OA,
∴∠OBC=∠AOB=60°,
∴△BOC为等边三角形,
∴∠COB=60°,
∴扇形OBC的面积==,
∴阴影部分的面积为.
故选B.
变式练4 D
母题5 A 提示:在Rt△ACB中,AB==2.
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,CD垂直平分AB,CD=BD=,
∴D为半圆的中点,
∴S阴影部分=S扇形ACB-S△ADC=π×22-×()2=π-1.
故选A.
变式练5 提示:由旋转的性质可知,△AED的面积=△ABC的面积,
∴图中阴影部分的面积=△AED的面积+扇形ADB的面积-△ABC的面积
=扇形ADB的面积
=
=.
故答案为.
母题6 π
变式练6 C 提示:n边形的内角和为(n-2)×180°,
圆形的空白部分的面积之和S==,
所以图中阴影部分的面积之和为5π-=.
故选C.
母题7 解:如图,在图中标注点E,连接BE,CE,并标注各部分的面积分别为m,n,阴影部分的面积为z,
由题意得4m+4n+z=12,①
2m+n=12-×12,②
3m+2n=12-2××12-××1,③
由③-②得,m+n=,④
将④代入①得z=.
变式练7 A 提示:正方形的对角线长为=2,
扇形的半径为=,
故两块空白部分的面积为22-π×()2=4-π,
所以四块空白部分的面积为2(4-π)=8-2π,
所以阴影部分的面积为22-(8-2π)=2π-4.
故选A.
母题8 解:(1)当正三角形ABC向右翻滚一周时,其中心O经过的路线是三条圆心角为120°的等弧,
所以其中心O经过的路程为×3=2πR.
(2)当正方形ABCD向右翻滚一周时,其中心O经过的路线是四条圆心角为90°的等弧,
所以其中心O经过的路程为×4=2πR.
(3)当正n边形向右翻滚一周时,其中心O经过的路线是n条圆心角为的等弧,
所以其中心O经过的路程为×n=2πR.
(4)是定值2πR,理由如下:
在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆☉ O的半径为R,把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,如图,当AC边与直线l重合时,点C与点C'重合,点A与点A'重合,点B与点B'重合,连接CO,C'O',则∠ACO=∠A'C'O',所以∠OCO'=∠ACA'=180°-γ,所以弧长为,
同理,另两条弧长分别为,,
所以外心O所经过的路程为++=2πR.
变式练8 解:正六边形的中心O运动的路程就是6个以正六边形顶点为圆心,正六边形的半径为半径旋转60°的弧长.
∵正六边形的边长为2 cm,
∴每次运动的路程长为=(cm).
∵从图1运动到图2共重复进行了六次上述的运动,
∴正六边形的中心O运动的路程长为6×=4π(cm).
任务一 弧长公式的应用
子任务1 弧长公式的实际应用
母题1 图中实线部分是半径为9 m的两条等弧组成的游泳池.若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为 ( )
A.12π m
B.18π m
C.20π m
D.24π m
变式练1:中国高铁的飞速发展,已成为中国式现代化建设的重要标志.如图,这是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.8千米,则这段圆曲线的长为 ( )
A. 千米 B. 千米
C. 千米 D. 千米
子任务2 求图形滚动问题中的路径长
母题2 如图,在矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线l做无滑动翻滚,当点A第一次翻滚到点A1位置时,点A经过的路线长为 .
【关键点拨】
变式练2:如图,在菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右做无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过45次这样的操作,菱形中心O所经过的路径总长为 .(结果保留π)
任务二 利用圆锥的侧面展开图求最短距离
母题3 如图,有一圆锥形粮仓,其正视图是边长为4 m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达
点P处捕捉老鼠,则小猫经过的最短路程为 ( )
A.5 m B.3 m
C.6 m D.2 m
变式练3:如图,圆锥的底面半径为2,母线AC的长为6,点D为AC的中点,一只蚂蚁从底面的点B处出发,沿着圆锥侧面爬到D处,则蚂蚁爬行的最短路线长为 .
任务三 不规则图形面积的求法
子任务1 等积变换法
母题4 如图,A是半径为1的☉O外的一点,OA=2,AB是☉O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于 ( )
A. B.
C.+ D.-
【关键点拨】
变式练4:如图,AB是☉O的直径,弦CD⊥AB,∠C=30°,CD=2,则阴影部分图形的面积为 ( )
A.4π B.2π
C.π D.
子任务2 割补法
母题5 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为 ( )
A.π-1 B.2π-1
C.2π-2 D.π-2
变式练5:如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为BD,则图中阴影部分的面积为 .
子任务3 化零为整法
母题6 如图,以四边形ABCD各个顶点为圆心,1 cm长为半径画弧,则图中阴影部分的面积之和是 cm2(结果保留π).
变式练6:如图,分别以五边形ABCDE的顶点为圆心,1为半径作五个圆,则图中阴影部分的面积之和为 ( )
A. B.3π
C. D.2π
子任务4 构造法
母题7 如图,正方形ABCD的边长为1,分别以正方形的四个顶点为圆心,边长为半径,在正方形内画圆弧,求图中阴影部分的面积.
变式练7:山西著名工艺品平遥推光漆器外观古朴雅致、闪光发亮,绘饰金碧辉煌,以手掌推出光泽而得名.图1是平遥推光漆器的一种图案,图2是选取其某部分并且放大后的示意图.四边形ABCD是边长为2的正方形,分别以正方形的四个顶点为圆心,对角线的长为半径画弧,四条弧相交于点O,则图中阴影部分的面积为 ( )
A.2π-4 B.π-2
C.2π D. π
任务四 与图形滚动有关的计算
母题8 归纳猜想:同学们,让我们一起进行一次研究性学习.
(1)如图1,已知正三角形ABC的中心为O,半径为R,将其沿直线l向右翻滚,当正三角形翻滚一周时,其中心O经过的路程是多少
图1
(2)如图2,将半径为R的正方形沿直线l向右翻滚,当正方形翻滚一周时,其中心O经过的路程是多少
图2
(3)猜想:如图3,把半径为R的正多边形沿直线l翻滚一周,其中心O所经过的路程是多少 请说明理由.
图3
(4)进一步猜想:当将任意圆的内接多边形沿直线l翻滚一周时,其外心所经过的路程是不是一个定值 为什么 请以任意三角形(如图4)为例说明.
图4
变式练8:如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2的位置,若正六边形的边长为2 cm,求正六边形的中心O运动的路程长.
参考答案
母题1 D
变式练1 C 提示:∵CA,CB是切线,
∴OA⊥AC,OB⊥CB,∴∠OAC=∠OBC=90°,∴∠AOB+∠ACB=180°,∵∠ACB+α=180°,∴∠AOB=α=60°,∴的长==.故选C.
母题2 6π 提示:∵四边形ABCD是矩形,AB=4,BC=3,
∴BC=AD=3,∠ADC=90°,对角线AC=BD=5.
∵根据旋转的性质知,∠ADA'=90°,AD=A'D=BC=3,
∴点A第一次翻滚到点A'位置时,点A经过的路线长为=,
同理,点A'第一次翻滚到点A″位置时,点A'经过的路线长为=2π,
点A″第一次翻滚到点A1位置时,点A″经过的路线长为=,
则当点A第一次翻滚到点A1位置时,点A经过的路线长为+2π+=6π.
故答案为6π.
变式练2 10π+5π 提示:在菱形ABCD中,AB=2,∠C=60°,
所以第一、二次旋转形成弧的半径是,圆心角是60°,
所以第一、二次旋转的弧长和=+=2×=,
因为第三次旋转形成弧的半径是1,圆心角是60°,
所以第三次旋转的弧长==,
因为一个周期为3,
所以45÷3=15,
所以菱形中心O所经过的路径总长为
15×=10π+5π.
故答案为10π+5π.
母题3 D 提示:设圆锥侧面展开图的圆心角为n.
∵圆锥形粮仓的正视图是边长为4 m的正△ABC,
∴圆锥的底面周长是4π,则4π=,
∴n=180°,即圆锥侧面展开图的圆心角是180°.
在圆锥侧面展开图中,AP=2,AB=4,∠BAP=90°.
∴BP===2 m,
故小猫经过的最短距离是2 m.故选D.
变式练3 3 提示:把圆锥沿母线AB展开得到它的侧面积为扇形BAB',C'点为弧BB'的中点,如图,
设∠BAB'=n°,
根据题意得,2π×2=,解得n=120,
∴∠BAC'=60°,
∴△BAC'为等边三角形,
∵点D为AC的中点,
∴点D'为AC'的中点,
∴BD'⊥AC',∴AD'=3,
∴BD'==3,
∴蚂蚁爬行的最短路线长为3.
故答案为3.
母题4 B 提示:如图,连接OB,OC,过点O作OD⊥BC于点D.
∵BC∥OA,
∴点A到BC的距离等于点O到BC的距离,
∴S△BOC=S△ABC,
∴阴影部分的面积=扇形OBC的面积.
∵AB是☉O的切线,
∴OB⊥AB.
∵OA=2,OB=OC=1,
∴∠OAB=30°,
∴∠AOB=60°.
又∵BC∥OA,
∴∠OBC=∠AOB=60°,
∴△BOC为等边三角形,
∴∠COB=60°,
∴扇形OBC的面积==,
∴阴影部分的面积为.
故选B.
变式练4 D
母题5 A 提示:在Rt△ACB中,AB==2.
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,CD垂直平分AB,CD=BD=,
∴D为半圆的中点,
∴S阴影部分=S扇形ACB-S△ADC=π×22-×()2=π-1.
故选A.
变式练5 提示:由旋转的性质可知,△AED的面积=△ABC的面积,
∴图中阴影部分的面积=△AED的面积+扇形ADB的面积-△ABC的面积
=扇形ADB的面积
=
=.
故答案为.
母题6 π
变式练6 C 提示:n边形的内角和为(n-2)×180°,
圆形的空白部分的面积之和S==,
所以图中阴影部分的面积之和为5π-=.
故选C.
母题7 解:如图,在图中标注点E,连接BE,CE,并标注各部分的面积分别为m,n,阴影部分的面积为z,
由题意得4m+4n+z=12,①
2m+n=12-×12,②
3m+2n=12-2××12-××1,③
由③-②得,m+n=,④
将④代入①得z=.
变式练7 A 提示:正方形的对角线长为=2,
扇形的半径为=,
故两块空白部分的面积为22-π×()2=4-π,
所以四块空白部分的面积为2(4-π)=8-2π,
所以阴影部分的面积为22-(8-2π)=2π-4.
故选A.
母题8 解:(1)当正三角形ABC向右翻滚一周时,其中心O经过的路线是三条圆心角为120°的等弧,
所以其中心O经过的路程为×3=2πR.
(2)当正方形ABCD向右翻滚一周时,其中心O经过的路线是四条圆心角为90°的等弧,
所以其中心O经过的路程为×4=2πR.
(3)当正n边形向右翻滚一周时,其中心O经过的路线是n条圆心角为的等弧,
所以其中心O经过的路程为×n=2πR.
(4)是定值2πR,理由如下:
在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆☉ O的半径为R,把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,如图,当AC边与直线l重合时,点C与点C'重合,点A与点A'重合,点B与点B'重合,连接CO,C'O',则∠ACO=∠A'C'O',所以∠OCO'=∠ACA'=180°-γ,所以弧长为,
同理,另两条弧长分别为,,
所以外心O所经过的路程为++=2πR.
变式练8 解:正六边形的中心O运动的路程就是6个以正六边形顶点为圆心,正六边形的半径为半径旋转60°的弧长.
∵正六边形的边长为2 cm,
∴每次运动的路程长为=(cm).
∵从图1运动到图2共重复进行了六次上述的运动,
∴正六边形的中心O运动的路程长为6×=4π(cm).
同课章节目录
