27.2 相似三角形同步培优训练(含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 27.2 相似三角形同步培优训练(含答案)2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 199.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:21:07 | ||
图片预览




文档简介
27.2 相似三角形
任务一 相似三角形的判定
母题1 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF与AD交于点E,与BC的延长线交于点F,连接AF.求证:△ABF∽△CAF.
变式练1:如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
任务二 相似三角形性质的应用
母题2 如图,在△ABC中,D,E分别为BC,AC边上的中点,AD,BE相交于点G.
若S△DEG=1,求S△ABC.
变式练2:如图,在 ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
(1)求证:△ABF∽△CEB.
(2)若△CEB的面积为9,求 ABCD的面积.
任务三 相似三角形的判定与性质的综合应用
母题3 如图,在△ABC中,点D在边BC上,连接AD,∠CDE=∠ADB,DE交边AC于点E,交BA的延长线于点F,且AD2=DE·DF.
求证:(1)△BFD∽△CAD;
(2)BF·DE=AB·AD.
变式练3:如图,在 ABCD中,AC,BD交于点O,M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN.
(2)求BD的长.
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
任务四 利用相似三角形解决实际问题
母题4 如图,直立在B处的标杆AB=2.4米,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8米,FB=2.5米,人高EF=1.5米,求树高CD.
变式练4:如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6 m,标杆FC=2.2 m,且BC=1m,CD=5m,FC,ED都垂直于地面,求电视塔的高ED.
任务五 与相似三角形有关的几何探究问题
母题5 证明体验
(1)如图1,AD为△ABC的角平分线,∠ADC=60°,点E在AB上,AE=AC.求证:DE平分∠ADB.
思考探究
(2)如图2,在(1)的条件下,F为AB上一点,连接FC交AD于点G.若FB=FC,DG=2,CD=3,求BD的长.
拓展延伸
(3)如图3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC.若BC=5,CD=2,AD=2AE,求AC的长.
图1 图2 图3
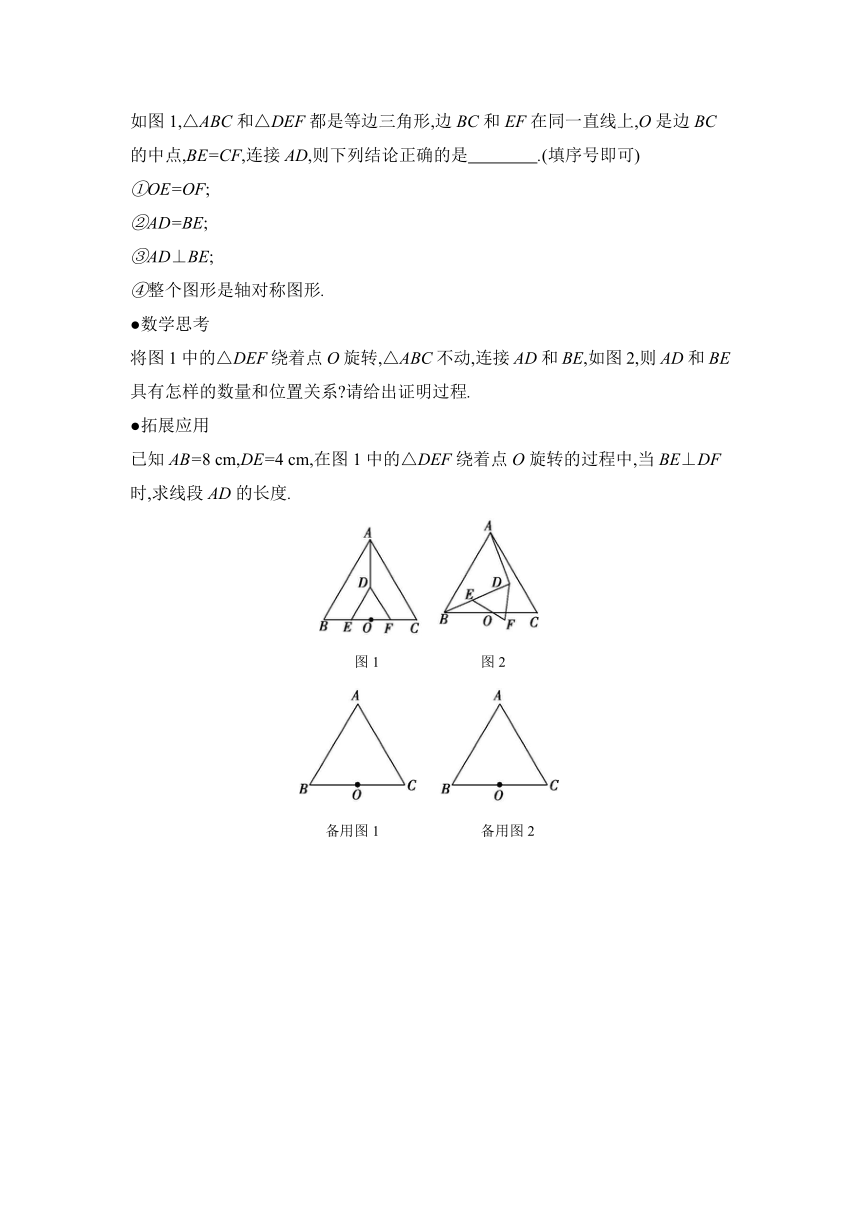
变式练5:●问题发现
如图1,△ABC和△DEF都是等边三角形,边BC和EF在同一直线上,O是边BC的中点,BE=CF,连接AD,则下列结论正确的是 .(填序号即可)
①OE=OF;
②AD=BE;
③AD⊥BE;
④整个图形是轴对称图形.
●数学思考
将图1中的△DEF绕着点O旋转,△ABC不动,连接AD和BE,如图2,则AD和BE具有怎样的数量和位置关系 请给出证明过程.
●拓展应用
已知AB=8 cm,DE=4 cm,在图1中的△DEF绕着点O旋转的过程中,当BE⊥DF时,求线段AD的长度.
图1 图2
备用图1 备用图2
参考答案
母题1 证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
∵EF垂直平分AD,
∴AF=DF,
∴∠ADF=∠DAF.
∵∠ACF=∠ADF+∠CAD,∠BAF=∠DAF+∠BAD,
∴∠ACF=∠BAF.
又∵∠CFA=∠AFB,
∴△ABF∽△CAF.
变式练1 证明:∵AD=DB,
∴∠B=∠EAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∠1=∠2,
∴∠C=∠ADE,
∴△ABC∽△EAD.
母题2 解:∵D,E分别为BC,AC边上的中点,
∴DE∥AB,DE=AB,
∴△AGB∽△DGE,
∴==,=2=2=4.
∵S△DEG=1,∴S△ABG=4.
∵△AEG中AG边上的高与△DEG中DG边上的高相等,
∴===2.
∴S△AEG=2.
同理可得S△DBG=2,
∴S四边形ABDE=S△ABG+S△AEG+S△DBG+S△DEG=4+2+2+1=9.
∵DE∥AB,∴△CED∽△CAB.
又∵DE=AB,
∴=2=2=,
∴S四边形ABDE∶S△ABC=3∶4,
∴S△ABC=12.
变式练2 解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,∴∠ABF=∠E.
在△ABF和△CEB中,∠A=∠C,∠ABF=∠E,
∴△ABF∽△CEB.
(2)∵AF=2FD,∴AD=3FD,
∴DF∶AD=1∶3.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴△ABF∽△DEF,△CEB∽△DEF,DF∶BC=1∶3,
∴S△ABF∶S△DEF=AF2∶FD2=4∶1,S△BCE∶S△FDE=BC2∶FD2=9∶1.
∵△CEB的面积为9,∴△FDE的面积为1,
∴△ABF的面积为4,
∴ ABCD的面积=9-1+4=12.
母题3 证明:(1)∵AD2=DE·DF,
∴=.
又∵∠ADF=∠EDA,
∴△ADF∽△EDA,
∴∠F=∠DAE.
∵∠ADB=∠CDE,
∴∠ADB+∠ADF=∠CDE+∠ADF,即∠BDF=∠CDA,
∴△BFD∽△CAD.
(2)∵△BFD∽△CAD,∴=.
∵=,∴=.
由(1)知,△BFD∽△CAD,
∴∠B=∠C,
∴AB=AC,
∴=,即BF·DE=AB·AD.
变式练3 解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠CBN,
∴△DMN∽△BCN.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,OB=OD=BD.
∵△DMN∽△BCN,∴=.
∵M为AD的中点,
∴AD=2DM,∴BC=2DM,
∴BN=2DN.
设OB=OD=x,
∴BD=2x,
∴BN=OB+ON=x+1,DN=OD-ON=x-1,
∴x+1=2(x-1),
解得x=3,
∴BD=2x=6,
∴BD的长为6.
(3)∵△MND∽△CNB,
∴DM∶BC=MN∶CN=DN∶BN=1∶2.
∵△DCN的面积为2,
∴S△MND=S△CND=1,S△BNC=2S△CND=4,
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5,
∴四边形ABNM的面积为5.
母题4 解:如图,过点E作EH⊥CD交CD于点H,交AB于点G.
由已知,得EF⊥FD,AB⊥FD,CD⊥FD.
∵易证四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB-GB=2.4-1.5=0.9(米).
∵EH⊥CD,EH⊥AB,∴AG∥CH,
∴△AEG∽△CEH,
∴=,∴=,
解得CH=3.78,
∴CD=CH+DH=3.78+1.5=5.28(米).
答:树高CD为5.28米.
变式练4 解:如图,过点A作AH⊥ED交ED于点H,交FC于点G.
∵FC⊥BD,ED⊥BD,AH⊥ED,AH⊥FG,
∴FG∥EH.
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC.
∵AB=1.6 m,FC=2.2 m,BC=1 m,CD=5 m,
∴FG=2.2-1.6=0.6 m,BD=6 m.
∵FG∥EH,∴=,即=,解得EH=3.6,
∴ED=3.6+1.6=5.2(m).
答:电视塔的高ED为5.2 m.
母题5 解:(1)证明:∵AD平分∠BAC,
∴∠EAD=∠CAD.
∵AE=AC,AD=AD,
∴△EAD≌△CAD(SAS),
∴∠ADE=∠ADC=60°,
∴∠EDB=180°-∠ADE-∠ADC=60°,
∴∠BDE=∠ADE,即DE平分∠ADB.
(2)∵FB=FC,
∴∠EBD=∠GCD.
∵∠BDE=∠CDG=60°,
∴△EBD∽△GCD,
∴=.
∵△EAD≌△CAD,
∴DE=DC=3.
∵DG=2,
∴BD=.
(3)如图,在AB上取一点F,使得AF=AD,连接CF.
∵AC平分∠BAD,
∴∠FAC=∠DAC.
∵AC=AC,AF=AD,
∴△AFC≌△ADC(SAS),
∴CF=CD,∠ACF=∠ACD,∠AFC=∠ADC.
∵∠ACF+∠BCF=∠ACB=2∠ACD,
∴∠DCE=∠BCF.
∵∠EDC=∠FBC,
∴△DCE∽△BCF,
∴=,∠CED=∠BFC.
∵BC=5,CF=CD=2,
∴CE=4.
∵∠AED=180°-∠CED=180°-∠BFC=∠AFC=∠ADC,
又∵∠EAD=∠DAC,
∴△EAD∽△DAC.
∵AD=2AE,
∴==,
∴AC=2AD=4AE,
∴AC=CE=.
变式练5 解:●问题发现:
①③④ 提示:∵O是边BC的中点,△ABC是等边三角形,
∴OB=OC.
又∵BE=CF,
∴OE=OF,∴①正确;
如图1,过点D作DG∥BE交AB于点G,
图1
∴∠AGD=∠B=60°,
∵△ABC和△DEF都是等边三角形,
∴∠B=∠DEF=60°.
∴BG∥DE,
∴四边形BEDG为平行四边形,
∴DG=BE≠AD,∴②不正确;
连接AO,DO,
∵△ABC和△DEF都是等边三角形,
∴AB=AC,DE=DF.
∵OB=OC,OE=OF,
∴AO⊥BC,DO⊥BC,
∴A,D,O三点共线,即AD⊥BE,∴③正确;
由③可知,整个图形关于直线AD成轴对称图形,∴④正确.
故答案为①③④.
●数学思考:AD=BE,AD⊥BE.证明如下:
如图2,连接AO,OD,由图1知,OB=OC,BE=CF,可得OE=OF.
图2
△DEF绕着点O旋转,OE=OF仍然成立.
∵△DEF是等边三角形,
∴DO⊥EF,∠EDO=∠EDF=30°,
∴OD=OE.
同理,AO⊥OB,OA=OB.
∴AO∶OB=DO∶EO=∶1,∠AOB=∠DOE,
∴∠BOE=∠AOD,∴△BOE∽△AOD,
∴AD=BE,∠OAD=∠OBE.
延长BE交AD于点H,交AO于点I,连接OH,
又∵∠AIH=BIO,∴△AIH∽△BIO,
∴∠AHI=∠IOB=90°,
∴AD⊥BE.
●拓展应用:
当BE⊥DF时,
∵AD⊥BE,
∴A,D,F三点共线.
如图3,连接AO,延长BE交AF于点H,
图3
设BE=x cm,
则AD=x cm,
∵AD⊥BE,
∴在Rt△ABH中,(x+2)2+(x+2)2=82.
解得x=-±.
又∵x>0,
∴x=-,
即AD=(3-3)cm.
如图4,设BE=y cm,则AD=y cm.
图4
∵AD⊥BE,
∴在Rt△ABH中,(y-2)2+(y-2)2=82,
解得y=±.
又y>0,
∴y=+,即AD=(3+3)cm.
综上所述,AD=(3±3)cm.
任务一 相似三角形的判定
母题1 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF与AD交于点E,与BC的延长线交于点F,连接AF.求证:△ABF∽△CAF.
变式练1:如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
任务二 相似三角形性质的应用
母题2 如图,在△ABC中,D,E分别为BC,AC边上的中点,AD,BE相交于点G.
若S△DEG=1,求S△ABC.
变式练2:如图,在 ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
(1)求证:△ABF∽△CEB.
(2)若△CEB的面积为9,求 ABCD的面积.
任务三 相似三角形的判定与性质的综合应用
母题3 如图,在△ABC中,点D在边BC上,连接AD,∠CDE=∠ADB,DE交边AC于点E,交BA的延长线于点F,且AD2=DE·DF.
求证:(1)△BFD∽△CAD;
(2)BF·DE=AB·AD.
变式练3:如图,在 ABCD中,AC,BD交于点O,M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN.
(2)求BD的长.
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
任务四 利用相似三角形解决实际问题
母题4 如图,直立在B处的标杆AB=2.4米,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8米,FB=2.5米,人高EF=1.5米,求树高CD.
变式练4:如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6 m,标杆FC=2.2 m,且BC=1m,CD=5m,FC,ED都垂直于地面,求电视塔的高ED.
任务五 与相似三角形有关的几何探究问题
母题5 证明体验
(1)如图1,AD为△ABC的角平分线,∠ADC=60°,点E在AB上,AE=AC.求证:DE平分∠ADB.
思考探究
(2)如图2,在(1)的条件下,F为AB上一点,连接FC交AD于点G.若FB=FC,DG=2,CD=3,求BD的长.
拓展延伸
(3)如图3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC.若BC=5,CD=2,AD=2AE,求AC的长.
图1 图2 图3
变式练5:●问题发现
如图1,△ABC和△DEF都是等边三角形,边BC和EF在同一直线上,O是边BC的中点,BE=CF,连接AD,则下列结论正确的是 .(填序号即可)
①OE=OF;
②AD=BE;
③AD⊥BE;
④整个图形是轴对称图形.
●数学思考
将图1中的△DEF绕着点O旋转,△ABC不动,连接AD和BE,如图2,则AD和BE具有怎样的数量和位置关系 请给出证明过程.
●拓展应用
已知AB=8 cm,DE=4 cm,在图1中的△DEF绕着点O旋转的过程中,当BE⊥DF时,求线段AD的长度.
图1 图2
备用图1 备用图2
参考答案
母题1 证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
∵EF垂直平分AD,
∴AF=DF,
∴∠ADF=∠DAF.
∵∠ACF=∠ADF+∠CAD,∠BAF=∠DAF+∠BAD,
∴∠ACF=∠BAF.
又∵∠CFA=∠AFB,
∴△ABF∽△CAF.
变式练1 证明:∵AD=DB,
∴∠B=∠EAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∠1=∠2,
∴∠C=∠ADE,
∴△ABC∽△EAD.
母题2 解:∵D,E分别为BC,AC边上的中点,
∴DE∥AB,DE=AB,
∴△AGB∽△DGE,
∴==,=2=2=4.
∵S△DEG=1,∴S△ABG=4.
∵△AEG中AG边上的高与△DEG中DG边上的高相等,
∴===2.
∴S△AEG=2.
同理可得S△DBG=2,
∴S四边形ABDE=S△ABG+S△AEG+S△DBG+S△DEG=4+2+2+1=9.
∵DE∥AB,∴△CED∽△CAB.
又∵DE=AB,
∴=2=2=,
∴S四边形ABDE∶S△ABC=3∶4,
∴S△ABC=12.
变式练2 解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,∴∠ABF=∠E.
在△ABF和△CEB中,∠A=∠C,∠ABF=∠E,
∴△ABF∽△CEB.
(2)∵AF=2FD,∴AD=3FD,
∴DF∶AD=1∶3.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴△ABF∽△DEF,△CEB∽△DEF,DF∶BC=1∶3,
∴S△ABF∶S△DEF=AF2∶FD2=4∶1,S△BCE∶S△FDE=BC2∶FD2=9∶1.
∵△CEB的面积为9,∴△FDE的面积为1,
∴△ABF的面积为4,
∴ ABCD的面积=9-1+4=12.
母题3 证明:(1)∵AD2=DE·DF,
∴=.
又∵∠ADF=∠EDA,
∴△ADF∽△EDA,
∴∠F=∠DAE.
∵∠ADB=∠CDE,
∴∠ADB+∠ADF=∠CDE+∠ADF,即∠BDF=∠CDA,
∴△BFD∽△CAD.
(2)∵△BFD∽△CAD,∴=.
∵=,∴=.
由(1)知,△BFD∽△CAD,
∴∠B=∠C,
∴AB=AC,
∴=,即BF·DE=AB·AD.
变式练3 解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠CBN,
∴△DMN∽△BCN.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,OB=OD=BD.
∵△DMN∽△BCN,∴=.
∵M为AD的中点,
∴AD=2DM,∴BC=2DM,
∴BN=2DN.
设OB=OD=x,
∴BD=2x,
∴BN=OB+ON=x+1,DN=OD-ON=x-1,
∴x+1=2(x-1),
解得x=3,
∴BD=2x=6,
∴BD的长为6.
(3)∵△MND∽△CNB,
∴DM∶BC=MN∶CN=DN∶BN=1∶2.
∵△DCN的面积为2,
∴S△MND=S△CND=1,S△BNC=2S△CND=4,
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5,
∴四边形ABNM的面积为5.
母题4 解:如图,过点E作EH⊥CD交CD于点H,交AB于点G.
由已知,得EF⊥FD,AB⊥FD,CD⊥FD.
∵易证四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB-GB=2.4-1.5=0.9(米).
∵EH⊥CD,EH⊥AB,∴AG∥CH,
∴△AEG∽△CEH,
∴=,∴=,
解得CH=3.78,
∴CD=CH+DH=3.78+1.5=5.28(米).
答:树高CD为5.28米.
变式练4 解:如图,过点A作AH⊥ED交ED于点H,交FC于点G.
∵FC⊥BD,ED⊥BD,AH⊥ED,AH⊥FG,
∴FG∥EH.
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC.
∵AB=1.6 m,FC=2.2 m,BC=1 m,CD=5 m,
∴FG=2.2-1.6=0.6 m,BD=6 m.
∵FG∥EH,∴=,即=,解得EH=3.6,
∴ED=3.6+1.6=5.2(m).
答:电视塔的高ED为5.2 m.
母题5 解:(1)证明:∵AD平分∠BAC,
∴∠EAD=∠CAD.
∵AE=AC,AD=AD,
∴△EAD≌△CAD(SAS),
∴∠ADE=∠ADC=60°,
∴∠EDB=180°-∠ADE-∠ADC=60°,
∴∠BDE=∠ADE,即DE平分∠ADB.
(2)∵FB=FC,
∴∠EBD=∠GCD.
∵∠BDE=∠CDG=60°,
∴△EBD∽△GCD,
∴=.
∵△EAD≌△CAD,
∴DE=DC=3.
∵DG=2,
∴BD=.
(3)如图,在AB上取一点F,使得AF=AD,连接CF.
∵AC平分∠BAD,
∴∠FAC=∠DAC.
∵AC=AC,AF=AD,
∴△AFC≌△ADC(SAS),
∴CF=CD,∠ACF=∠ACD,∠AFC=∠ADC.
∵∠ACF+∠BCF=∠ACB=2∠ACD,
∴∠DCE=∠BCF.
∵∠EDC=∠FBC,
∴△DCE∽△BCF,
∴=,∠CED=∠BFC.
∵BC=5,CF=CD=2,
∴CE=4.
∵∠AED=180°-∠CED=180°-∠BFC=∠AFC=∠ADC,
又∵∠EAD=∠DAC,
∴△EAD∽△DAC.
∵AD=2AE,
∴==,
∴AC=2AD=4AE,
∴AC=CE=.
变式练5 解:●问题发现:
①③④ 提示:∵O是边BC的中点,△ABC是等边三角形,
∴OB=OC.
又∵BE=CF,
∴OE=OF,∴①正确;
如图1,过点D作DG∥BE交AB于点G,
图1
∴∠AGD=∠B=60°,
∵△ABC和△DEF都是等边三角形,
∴∠B=∠DEF=60°.
∴BG∥DE,
∴四边形BEDG为平行四边形,
∴DG=BE≠AD,∴②不正确;
连接AO,DO,
∵△ABC和△DEF都是等边三角形,
∴AB=AC,DE=DF.
∵OB=OC,OE=OF,
∴AO⊥BC,DO⊥BC,
∴A,D,O三点共线,即AD⊥BE,∴③正确;
由③可知,整个图形关于直线AD成轴对称图形,∴④正确.
故答案为①③④.
●数学思考:AD=BE,AD⊥BE.证明如下:
如图2,连接AO,OD,由图1知,OB=OC,BE=CF,可得OE=OF.
图2
△DEF绕着点O旋转,OE=OF仍然成立.
∵△DEF是等边三角形,
∴DO⊥EF,∠EDO=∠EDF=30°,
∴OD=OE.
同理,AO⊥OB,OA=OB.
∴AO∶OB=DO∶EO=∶1,∠AOB=∠DOE,
∴∠BOE=∠AOD,∴△BOE∽△AOD,
∴AD=BE,∠OAD=∠OBE.
延长BE交AD于点H,交AO于点I,连接OH,
又∵∠AIH=BIO,∴△AIH∽△BIO,
∴∠AHI=∠IOB=90°,
∴AD⊥BE.
●拓展应用:
当BE⊥DF时,
∵AD⊥BE,
∴A,D,F三点共线.
如图3,连接AO,延长BE交AF于点H,
图3
设BE=x cm,
则AD=x cm,
∵AD⊥BE,
∴在Rt△ABH中,(x+2)2+(x+2)2=82.
解得x=-±.
又∵x>0,
∴x=-,
即AD=(3-3)cm.
如图4,设BE=y cm,则AD=y cm.
图4
∵AD⊥BE,
∴在Rt△ABH中,(y-2)2+(y-2)2=82,
解得y=±.
又y>0,
∴y=+,即AD=(3+3)cm.
综上所述,AD=(3±3)cm.
