27.3 位似 同步培优训练(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 27.3 位似 同步培优训练(含答案) 2024-2025学年数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 320.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:21:32 | ||
图片预览


文档简介
27.3 位似
任务一 平面直角坐标系中的位似变换
子任务1 位似中心是坐标原点
母题1 如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形△OB'C'.
(2)按(1)的方式得到的B点的对应点B'的坐标是 ;C点的对应点C'的坐标是 .
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P'的坐标是 .
变式练1:如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,位似比为2∶1,在y轴的左侧画出△ABC放大后的△A1B1C1.
(2)在(1)中,若M(m,n)为线段BC上任一点,则变化后点M的对应点M'的坐标为 .
(3)直接写出△A1B1C1外接圆的圆心D的坐标: .
子任务2 位似中心不是坐标原点
母题2 如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B'的横坐标是 .
变式练2:如图,在平面直角坐标系中,△ABC的顶点A在第二象限,点B的坐标为(-2,0),点C的坐标为(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C.若点A的对应点A'的坐标为(2,-3),点B的对应点B'的坐标为(1,0),则点A的坐标为 ( )
A.(-3,2) B.-3,
C.-, D.-,2
任务二 与位似图形有关的分类讨论问题
母题3 如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是 .
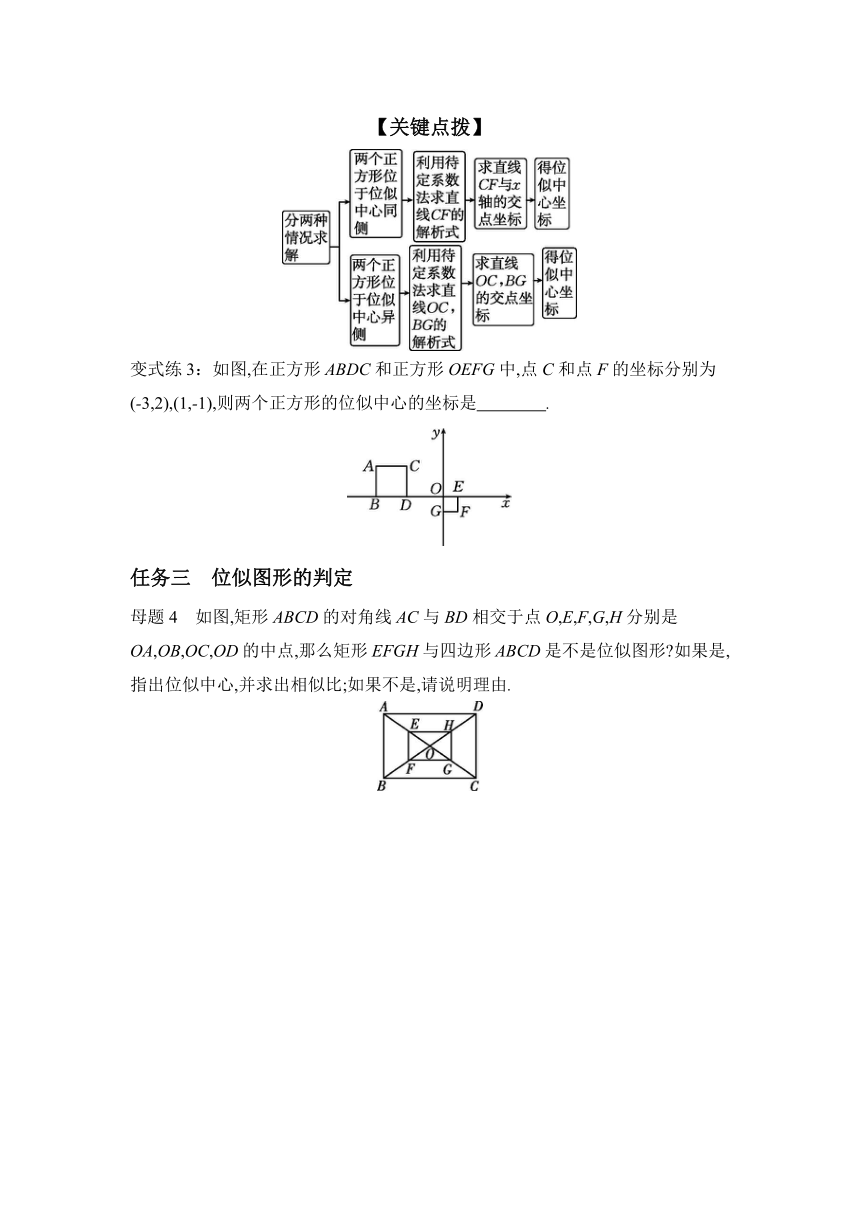
【关键点拨】
变式练3:如图,在正方形ABDC和正方形OEFG中,点C和点F的坐标分别为(-3,2),(1,-1),则两个正方形的位似中心的坐标是 .
任务三 位似图形的判定
母题4 如图,矩形ABCD的对角线AC与BD相交于点O,E,F,G,H分别是OA,OB,OC,OD的中点,那么矩形EFGH与四边形ABCD是不是位似图形 如果是,指出位似中心,并求出相似比;如果不是,请说明理由.
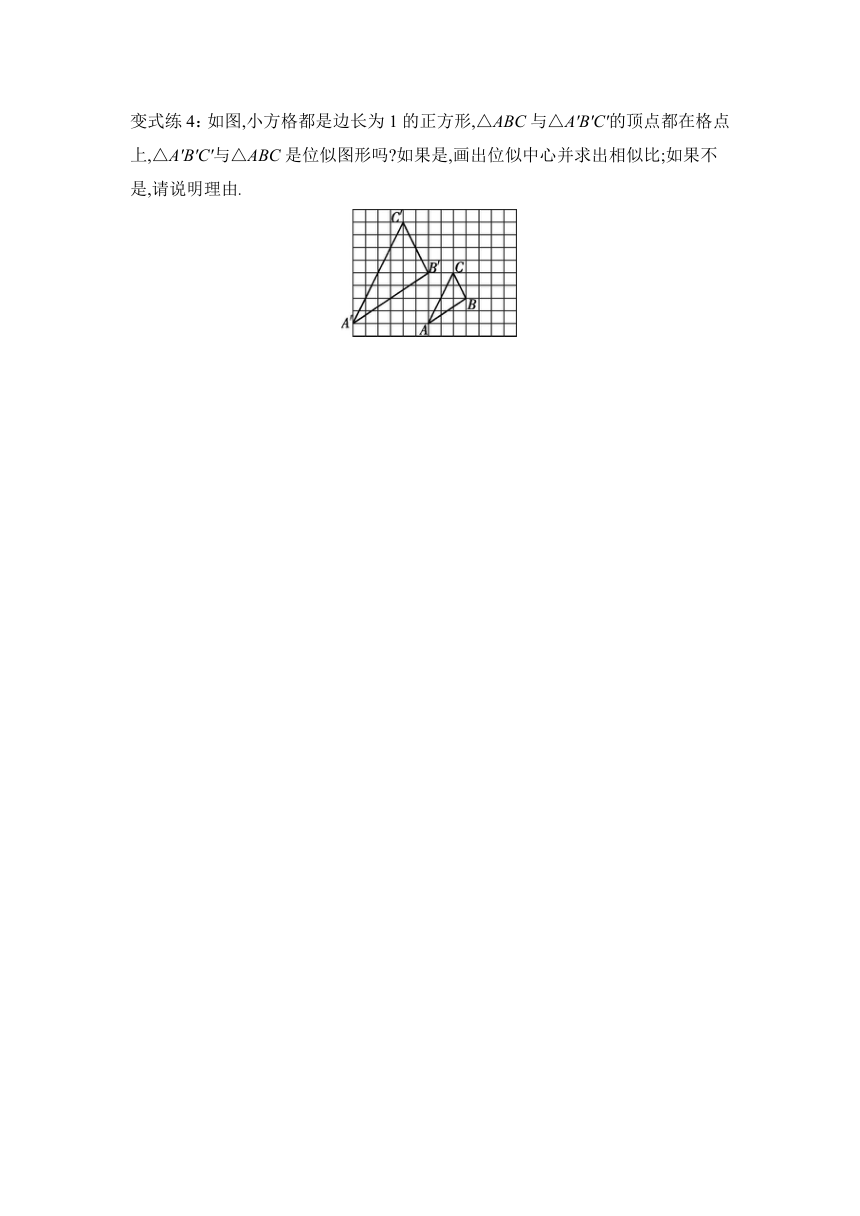
变式练4:如图,小方格都是边长为1的正方形,△ABC与△A'B'C'的顶点都在格点上,△A'B'C'与△ABC是位似图形吗 如果是,画出位似中心并求出相似比;如果不是,请说明理由.
参考答案
母题1 解:(1)如图,△OB'C'为所作.
(2)B点的对应点B'的坐标是(-6,2);C点的对应点C'的坐标是(-4,-2).
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P'的坐标为(-2x,-2y).
变式练1 解:(1)根据以原点O为位似中心的坐标变换规律,可得点A1,B1,C1的坐标分别为A1(-4,2),B1(-2,8),C1(-6,4),描点即可得到图中所示图形△A1B1C1.
(2)根据位似比和以原点O为位似中心的坐标变换规律可得,点M'的坐标为(2m,2n).
(3)如图所示,由网格的特点可得,∠A1C1B1=90°.
∵△A1B1C1是直角三角形,∴A1B1是圆的直径,
∴A1B1的中点即为△A1B1C1外接圆的圆心,
∴点D的坐标为(-3,5).
母题2 3-2a 提示:过点B作BD⊥x轴于点D,B'E⊥x轴于点E,
则BD∥B'E,
∴△BCD∽△B'CE,
∴==.
∵点C的坐标是(1,0),
∴OC=1.
∵点B的横坐标是a,
∴CD=a-1,
∴CE=2CD=2a-2,
∴OE=2a-3,
∴点B的对应点B'的横坐标是3-2a.
故答案为3-2a.
变式练2 C 提示:如图,过点A作AE⊥x轴于E,过点A'作A'F⊥x轴于F.
∵B(-2,0),C(-1,0),B'(1,0),A'(2,-3),
∴OB=2,OC=OB'=1,OF=2,A'F=3,
∴BC=1,CB'=2,CF=3.
∵△ABC∽△A'B'C,
∴==,
∴AE=.
∵∠ACE=∠A'CF,∠AEC=∠A'FC=90°,
∴△AEC∽△A'FC,
∴==,
∴EC=,
∴OE=EC+OC=,
∴A-,.
故选C.
母题3 (-2,0)或, 提示:如图,当两个图形位似时,①位似中心就是CF与x轴的交点.
设直线CF的解析式为y=kx+b,
将C(4,2),F(1,1)代入,
得解得即y=x+.
令y=0,得x=-2,
∴点O'的坐标是(-2,0).
②OC和BG的交点也是位似中心.
直线BG的解析式为y=-x+1,直线OC的解析式为y=x,
由解得
∴位似中心的坐标是,.
故答案为(-2,0)或,.
变式练3 (-1,0)或(5,-2) 提示:∵四边形ABDC和四边形OEFG是正方形,点C和点F的坐标分别为(-3,2),(1,-1),
∴A(-5,2),B(-5,0),E(1,0),G(0,-1).
设直线AF的解析式为y=k1x+b1(k1≠0),
把A(-5,2),F(1,-1)代入y=k1x+b1(k1≠0),
得解得
∴直线AF的解析式为y=-x-.
设直线CG的解析式为y=k2+b2(k2≠0),
把 G(0,-1),C(-3,2)代入y=k2x+b2(k2≠0),
得解得
∴直线CG的解析式为y=-x-1.
①如图1,当两个正方形位于位似中心异侧时,直线AF和直线CG的交点即为位似中心,
由解得
∴位似中心的坐标为(-1,0).
②如图2,当两个正方形位于位似中心同侧时,连接CE,DF并延长,CE与DF交于点M,过点M作MN⊥x轴于点N.
∵C(-3,2),F(1,-1),
∴位似比为2∶1,
∴EF=CD,即EF是△MCD的中位线,
∴CE=EM.
又∵∠CED=∠MEN,∠CDE=∠MNE=90°,
∴△CDE≌△MNE(AAS),
∴EN=DE=DO+OE=3+1=4,MN=CD=2,
∴ON=OE+EN=1+4=5,
∴点M的坐标为(5,-2).
故答案为(-1,0)或(5,-2).
图1 图2
母题4 解:∵E,F,G,H分别是OA,OB,OC,OD的中点,
∴EF AB,GH DC.
又∵四边形ABCD是矩形,
∴AB CD,∠BAD=90°,
∴EF∥GH,EF=GH,∠FEH=90°,
∴四边形EFGH是矩形.
又∵====,
∴矩形EFGH与矩形ABCD相似,且相似比为.
又∵两个图形的对应点所在直线都经过点O,
∴它们是位似图形,位似中心是点O,相似比为.
变式练4 解:由勾股定理,得AB==,
BC==,AC==2,
A'B'==2,B'C'==2,
A'C'==4.
∵=2,=2,=2,
∴==,
∴△ABC∽△A'B'C'.
如图,两个图形的对应点所在直线都经过点O,
∴△A'B'C'与△ABC是位似图形,点O为位似中心.
∵OA'=12,OA=6,
∴相似比为==2.
任务一 平面直角坐标系中的位似变换
子任务1 位似中心是坐标原点
母题1 如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形△OB'C'.
(2)按(1)的方式得到的B点的对应点B'的坐标是 ;C点的对应点C'的坐标是 .
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P'的坐标是 .
变式练1:如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,位似比为2∶1,在y轴的左侧画出△ABC放大后的△A1B1C1.
(2)在(1)中,若M(m,n)为线段BC上任一点,则变化后点M的对应点M'的坐标为 .
(3)直接写出△A1B1C1外接圆的圆心D的坐标: .
子任务2 位似中心不是坐标原点
母题2 如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B'的横坐标是 .
变式练2:如图,在平面直角坐标系中,△ABC的顶点A在第二象限,点B的坐标为(-2,0),点C的坐标为(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C.若点A的对应点A'的坐标为(2,-3),点B的对应点B'的坐标为(1,0),则点A的坐标为 ( )
A.(-3,2) B.-3,
C.-, D.-,2
任务二 与位似图形有关的分类讨论问题
母题3 如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是 .
【关键点拨】
变式练3:如图,在正方形ABDC和正方形OEFG中,点C和点F的坐标分别为(-3,2),(1,-1),则两个正方形的位似中心的坐标是 .
任务三 位似图形的判定
母题4 如图,矩形ABCD的对角线AC与BD相交于点O,E,F,G,H分别是OA,OB,OC,OD的中点,那么矩形EFGH与四边形ABCD是不是位似图形 如果是,指出位似中心,并求出相似比;如果不是,请说明理由.
变式练4:如图,小方格都是边长为1的正方形,△ABC与△A'B'C'的顶点都在格点上,△A'B'C'与△ABC是位似图形吗 如果是,画出位似中心并求出相似比;如果不是,请说明理由.
参考答案
母题1 解:(1)如图,△OB'C'为所作.
(2)B点的对应点B'的坐标是(-6,2);C点的对应点C'的坐标是(-4,-2).
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P'的坐标为(-2x,-2y).
变式练1 解:(1)根据以原点O为位似中心的坐标变换规律,可得点A1,B1,C1的坐标分别为A1(-4,2),B1(-2,8),C1(-6,4),描点即可得到图中所示图形△A1B1C1.
(2)根据位似比和以原点O为位似中心的坐标变换规律可得,点M'的坐标为(2m,2n).
(3)如图所示,由网格的特点可得,∠A1C1B1=90°.
∵△A1B1C1是直角三角形,∴A1B1是圆的直径,
∴A1B1的中点即为△A1B1C1外接圆的圆心,
∴点D的坐标为(-3,5).
母题2 3-2a 提示:过点B作BD⊥x轴于点D,B'E⊥x轴于点E,
则BD∥B'E,
∴△BCD∽△B'CE,
∴==.
∵点C的坐标是(1,0),
∴OC=1.
∵点B的横坐标是a,
∴CD=a-1,
∴CE=2CD=2a-2,
∴OE=2a-3,
∴点B的对应点B'的横坐标是3-2a.
故答案为3-2a.
变式练2 C 提示:如图,过点A作AE⊥x轴于E,过点A'作A'F⊥x轴于F.
∵B(-2,0),C(-1,0),B'(1,0),A'(2,-3),
∴OB=2,OC=OB'=1,OF=2,A'F=3,
∴BC=1,CB'=2,CF=3.
∵△ABC∽△A'B'C,
∴==,
∴AE=.
∵∠ACE=∠A'CF,∠AEC=∠A'FC=90°,
∴△AEC∽△A'FC,
∴==,
∴EC=,
∴OE=EC+OC=,
∴A-,.
故选C.
母题3 (-2,0)或, 提示:如图,当两个图形位似时,①位似中心就是CF与x轴的交点.
设直线CF的解析式为y=kx+b,
将C(4,2),F(1,1)代入,
得解得即y=x+.
令y=0,得x=-2,
∴点O'的坐标是(-2,0).
②OC和BG的交点也是位似中心.
直线BG的解析式为y=-x+1,直线OC的解析式为y=x,
由解得
∴位似中心的坐标是,.
故答案为(-2,0)或,.
变式练3 (-1,0)或(5,-2) 提示:∵四边形ABDC和四边形OEFG是正方形,点C和点F的坐标分别为(-3,2),(1,-1),
∴A(-5,2),B(-5,0),E(1,0),G(0,-1).
设直线AF的解析式为y=k1x+b1(k1≠0),
把A(-5,2),F(1,-1)代入y=k1x+b1(k1≠0),
得解得
∴直线AF的解析式为y=-x-.
设直线CG的解析式为y=k2+b2(k2≠0),
把 G(0,-1),C(-3,2)代入y=k2x+b2(k2≠0),
得解得
∴直线CG的解析式为y=-x-1.
①如图1,当两个正方形位于位似中心异侧时,直线AF和直线CG的交点即为位似中心,
由解得
∴位似中心的坐标为(-1,0).
②如图2,当两个正方形位于位似中心同侧时,连接CE,DF并延长,CE与DF交于点M,过点M作MN⊥x轴于点N.
∵C(-3,2),F(1,-1),
∴位似比为2∶1,
∴EF=CD,即EF是△MCD的中位线,
∴CE=EM.
又∵∠CED=∠MEN,∠CDE=∠MNE=90°,
∴△CDE≌△MNE(AAS),
∴EN=DE=DO+OE=3+1=4,MN=CD=2,
∴ON=OE+EN=1+4=5,
∴点M的坐标为(5,-2).
故答案为(-1,0)或(5,-2).
图1 图2
母题4 解:∵E,F,G,H分别是OA,OB,OC,OD的中点,
∴EF AB,GH DC.
又∵四边形ABCD是矩形,
∴AB CD,∠BAD=90°,
∴EF∥GH,EF=GH,∠FEH=90°,
∴四边形EFGH是矩形.
又∵====,
∴矩形EFGH与矩形ABCD相似,且相似比为.
又∵两个图形的对应点所在直线都经过点O,
∴它们是位似图形,位似中心是点O,相似比为.
变式练4 解:由勾股定理,得AB==,
BC==,AC==2,
A'B'==2,B'C'==2,
A'C'==4.
∵=2,=2,=2,
∴==,
∴△ABC∽△A'B'C'.
如图,两个图形的对应点所在直线都经过点O,
∴△A'B'C'与△ABC是位似图形,点O为位似中心.
∵OA'=12,OA=6,
∴相似比为==2.
