28.1 锐角三角函数 同步培优训练(含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 28.1 锐角三角函数 同步培优训练(含答案)2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 352.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 00:00:00 | ||
图片预览




文档简介
28.1 锐角三角函数
任务一 求锐角三角函数值
子任务1 利用参数法求锐角三角函数值
母题1 如图,在Rt△ABC中,∠C=90°,BC=3AC,则tan B= ( )
A.
B.3
C.
D.
变式练1:在直角三角形ABC中,若2AB=AC,则cos C的值为 ( )
A.或
B.或
C.或
D.或
子任务2 构造直角三角形求锐角三角函数值
母题2 如图,已知钝角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC=,求tan D的值.
变式练2:如图,△ABC与△BDC均为直角三角形,若∠ACB=30°,∠DBC=45°,求∠ADB的正切值.
母题3 如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为 ( )
A. B.
C. D.
变式练3:如图,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连接AC.若tan B=,则tan∠CAD的值为 .
子任务3 利用等角转换法求锐角三角函数值
母题4 如图,在半径为3的☉O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tan D= ( )
A.2 B.
C. D.
【关键点拨】
变式练4:如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,求sin∠BPC.
子任务4 利用网格求锐角三角函数值
母题5 如图,这是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是 .
【关键点拨】
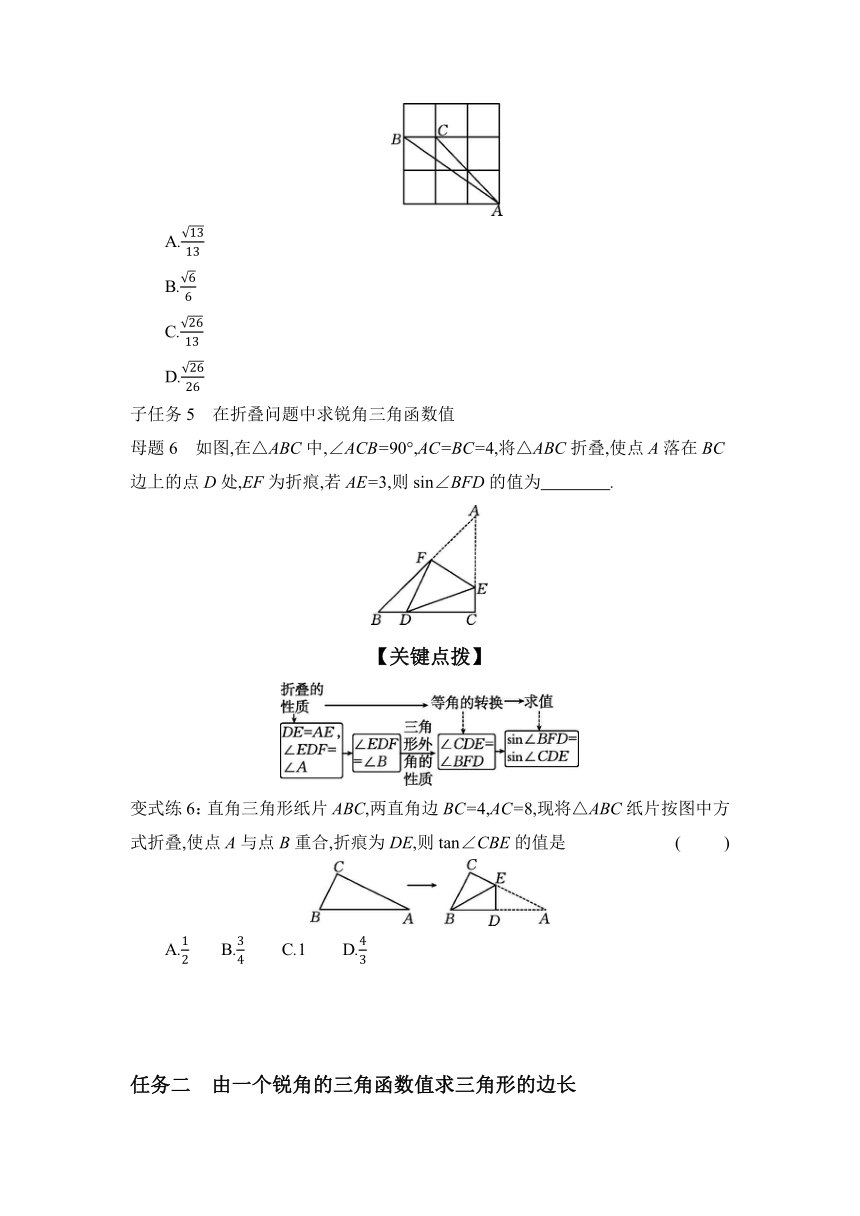
变式练5:如图,点A,B,C在正方形网格的格点上,则sin∠BAC= ( )
A.
B.
C.
D.
子任务5 在折叠问题中求锐角三角函数值
母题6 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为 .
【关键点拨】
变式练6:直角三角形纸片ABC,两直角边BC=4,AC=8,现将△ABC纸片按图中方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 ( )
A. B. C.1 D.
任务二 由一个锐角的三角函数值求三角形的边长
母题7 在Rt△ABC中,∠C=90°,sin A=,AC=8 cm,则BC的长度为 ( )
A.3 cm B.4 cm
C.5 cm D.6 cm
变式练7:已知∠A是锐角,sin A=,则cos A的值为 ( )
A. B. C. D.
任务三 由一个锐角的三角函数值求三角形的面积
母题8 已知△ABC中,tan B=,BC=6,过点A作BC边上的高,垂足为点D,且满足BD∶CD=2∶1,则△ABC面积的所有可能值为 .
变式练8:在△ABC中,AB=3,AC=6,∠B=45°,则BC= .
任务四 锐角三角函数的探究问题
母题9 如图1,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sin A=,sin B=,∴c=,c=,
∴=.
根据你掌握的三角函数知识,在图2的锐角三角形ABC中,探究,,之间的关系,并写出探究过程.
图1 图2
变式练9:把(sin α)2记作sin2α,根据图完成下列各题:
图1
图2
(1)如图1,sin2A1+cos2A1= ,sin2A2+cos2A2= ,
sin2A3+cos2A3= .
(2)观察上述等式后猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A= .
(3)如图2,在Rt△ABC中证明(2)题中的猜想.
(4)已知在△ABC中,∠A+∠B=90°,且sin A=,求cos A的值.
参考答案
母题1 A 提示:在Rt△ABC中,∠C=90°,BC=3AC,
∴tan B===.
故选A.
变式练1 C 提示:①当AC为直角边时,
∵2AB=AC,
∴BC==AB,
∴cos C===;
②当AC为斜边时,
∵2AB=AC,
∴BC==AB,
∴cos C===.
综上,cos C=或.
故选C.
母题2 解:∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
∴∠CAD=∠D,
∴CA=CD.
∵∠DAB=90°,
∴∠B+∠D=90°,∠BAC+∠CAD=90°,
∴∠B=∠BAC,
∴AC=CB,
∴BD=2AC=2×=3.
在Rt△ABD中,∵∠DAB=90°,AD=2,
∴AB==,
∴tan D==.
变式练2
解:如图,过点A作DB延长线的垂线,垂足为点E,
则∠E=90°,∠ABE=45°,AE=BE.
设AE=BE=x,则AB=x,BC=x,BD=CD=x,
∴DE=x+x,∴tan∠ADB====.
母题3 D 提示:如图,过点A作AD⊥BC,垂足为D,
在Rt△ACD中,CD=CA·cos C=1,
∴AD==.
在Rt△ABD中,BD=CB-CD=3,AD=.
∴AB==2.
∴sin B==.故选D.
变式练3 提示:如图,延长AD,过点C作CE⊥AD,垂足为E.
在Rt△BAD中,tan B==.
可设AD=5x,则AB=3x.
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴===,
∴CE=x,DE=x,
∴AE=AD+DE=x,
∴在Rt△AEC中,tan∠CAD==.
故答案为.
母题4 A 提示:如图,连接BC.
∵AB是直径,∴∠ACB=90°.
∵☉O的半径为3,∴AB=6,
∴BC===4,
∴tan D=tan A===2.
故选A.
变式练4 解:如图,作AD⊥BC于点D.
∵AB=AC=5,BC=8,
∴BD=CD=4,∠BAD=∠BAC.
∵∠ADB=90°,∴sin∠BAD==.
又∵∠BPC=∠BAC,
∴∠BPC=∠BAD,
∴sin∠BPC=.
母题5 2 提示:如图,过点Q作QC∥BA,连接PC,
∴∠QMB=∠CQP.
由题意得CQ2=22+22=8,
PC2=42+42=32,
PQ2=22+62=40,
∴PC2+CQ2=PQ2,
∴△PCQ是直角三角形,
∴∠PCQ=90°,
∴tan∠CQP===2,
∴tan∠QMB=tan∠CQP=2.
故答案为2.
变式练5 D 提示:如图,延长AC到点D,连接BE交CD于点O,
∴BE⊥CD,AB==,OB=BE==,
∴sin∠BAC===.
故选D.
母题6 提示:∵在△ABC中,∠ACB=90°,AC=BC=4,
∴∠A=∠B.
由折叠的性质得到△AEF≌△DEF,
∴∠EDF=∠A,
∴∠EDF=∠B,
∴∠CDE+∠BDF+∠EDF=∠BFD+∠BDF+∠B=180°,
∴∠CDE=∠BFD.
又∵AE=DE=3,
∴CE=4-3=1.
在直角△ECD中,sin∠CDE==,
∴sin∠BFD=.
故答案为.
变式练6 B 提示:根据题意,BE=AE.设BE=x,则CE=8-x.
在Rt△BCE中,x2=(8-x)2+42,
解得x=5,
∴CE=8-5=3,
∴tan∠CBE==.
故选B.
母题7 D 提示:∵sin A==,
∴设BC=3x,AB=5x.
又∵AC2+BC2=AB2,
∴82+(3x)2=(5x)2,
解得x=2或x=-2(舍去),
∴BC=3x=6 cm.
故选D.
变式练7 B 提示:∵sin2A+cos2A=1,
∴cos A==.
故选B.
母题8 8或24 提示:如图1所示,
∵BC=6,BD∶CD=2∶1,
∴BD=4.
∵AD⊥BC,tan B=,
∴=,
∴AD=BD=,
∴S△ABC=BC AD=×6×=8.
如图2所示,
∵BC=6,BD∶CD=2∶1,∴BD=12.
∵AD⊥BC,tan B=,∴=,∴AD=BD=8,
∴S△ABC=BC AD=×6×8=24.
综上所述,△ABC面积的所有可能值为8或24.
故答案为8或24.
图1 图2
变式练8 3+3或3-3 提示:①当△ABC为锐角三角形时,
过点A作AD⊥BC于点D,如图1.
图1
∵AB=3,∠B=45°,
∴AD=BD=AB·sin 45°=3,
∴CD==3,∴BC=BD+CD=3+3.
②当△ABC为钝角三角形时,
过点A作AD⊥BC交BC延长线于点D,如图2.
图2
∵AB=3,∠B=45°,
∴AD=BD=AB·sin 45°=3,
∴CD==3,
∴BC=BD-CD=3-3.
综上,BC的长为3+3或3-3.
故答案为3+3或3-3.
母题9 解:==.理由如下:如图,过点A作AD⊥BC,过点B作BE⊥AC,
在Rt△ABD中,sin B=,即AD=csin B,
在Rt△ADC中,sin C=,即AD=bsin C,
∴csin B=bsin C,即=,
同理可得=,
则==.
变式练9 解:(1)1;1;1 提示:sin2A1+cos2A1=2+2=+=1,
sin2A2+cos2A2=2+2=+=1,
sin2A3+cos2A3=2+2=+=1.故答案为1;1;1.
(2)1.
(3)在题图2中,∵sin A=,cos A=,且a2+b2=c2,
则sin2A+cos2A=2+2=+===1,
即sin2A+cos2A=1.
(4)在△ABC中,∠A+∠B=90°,∴∠C=90°.
∵sin2A+cos2A=1,∴2+cos2A=1,
解得cos A=或cos A=-(舍去),∴cos A=.
任务一 求锐角三角函数值
子任务1 利用参数法求锐角三角函数值
母题1 如图,在Rt△ABC中,∠C=90°,BC=3AC,则tan B= ( )
A.
B.3
C.
D.
变式练1:在直角三角形ABC中,若2AB=AC,则cos C的值为 ( )
A.或
B.或
C.或
D.或
子任务2 构造直角三角形求锐角三角函数值
母题2 如图,已知钝角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC=,求tan D的值.
变式练2:如图,△ABC与△BDC均为直角三角形,若∠ACB=30°,∠DBC=45°,求∠ADB的正切值.
母题3 如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为 ( )
A. B.
C. D.
变式练3:如图,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连接AC.若tan B=,则tan∠CAD的值为 .
子任务3 利用等角转换法求锐角三角函数值
母题4 如图,在半径为3的☉O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tan D= ( )
A.2 B.
C. D.
【关键点拨】
变式练4:如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,求sin∠BPC.
子任务4 利用网格求锐角三角函数值
母题5 如图,这是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是 .
【关键点拨】
变式练5:如图,点A,B,C在正方形网格的格点上,则sin∠BAC= ( )
A.
B.
C.
D.
子任务5 在折叠问题中求锐角三角函数值
母题6 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为 .
【关键点拨】
变式练6:直角三角形纸片ABC,两直角边BC=4,AC=8,现将△ABC纸片按图中方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 ( )
A. B. C.1 D.
任务二 由一个锐角的三角函数值求三角形的边长
母题7 在Rt△ABC中,∠C=90°,sin A=,AC=8 cm,则BC的长度为 ( )
A.3 cm B.4 cm
C.5 cm D.6 cm
变式练7:已知∠A是锐角,sin A=,则cos A的值为 ( )
A. B. C. D.
任务三 由一个锐角的三角函数值求三角形的面积
母题8 已知△ABC中,tan B=,BC=6,过点A作BC边上的高,垂足为点D,且满足BD∶CD=2∶1,则△ABC面积的所有可能值为 .
变式练8:在△ABC中,AB=3,AC=6,∠B=45°,则BC= .
任务四 锐角三角函数的探究问题
母题9 如图1,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sin A=,sin B=,∴c=,c=,
∴=.
根据你掌握的三角函数知识,在图2的锐角三角形ABC中,探究,,之间的关系,并写出探究过程.
图1 图2
变式练9:把(sin α)2记作sin2α,根据图完成下列各题:
图1
图2
(1)如图1,sin2A1+cos2A1= ,sin2A2+cos2A2= ,
sin2A3+cos2A3= .
(2)观察上述等式后猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A= .
(3)如图2,在Rt△ABC中证明(2)题中的猜想.
(4)已知在△ABC中,∠A+∠B=90°,且sin A=,求cos A的值.
参考答案
母题1 A 提示:在Rt△ABC中,∠C=90°,BC=3AC,
∴tan B===.
故选A.
变式练1 C 提示:①当AC为直角边时,
∵2AB=AC,
∴BC==AB,
∴cos C===;
②当AC为斜边时,
∵2AB=AC,
∴BC==AB,
∴cos C===.
综上,cos C=或.
故选C.
母题2 解:∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
∴∠CAD=∠D,
∴CA=CD.
∵∠DAB=90°,
∴∠B+∠D=90°,∠BAC+∠CAD=90°,
∴∠B=∠BAC,
∴AC=CB,
∴BD=2AC=2×=3.
在Rt△ABD中,∵∠DAB=90°,AD=2,
∴AB==,
∴tan D==.
变式练2
解:如图,过点A作DB延长线的垂线,垂足为点E,
则∠E=90°,∠ABE=45°,AE=BE.
设AE=BE=x,则AB=x,BC=x,BD=CD=x,
∴DE=x+x,∴tan∠ADB====.
母题3 D 提示:如图,过点A作AD⊥BC,垂足为D,
在Rt△ACD中,CD=CA·cos C=1,
∴AD==.
在Rt△ABD中,BD=CB-CD=3,AD=.
∴AB==2.
∴sin B==.故选D.
变式练3 提示:如图,延长AD,过点C作CE⊥AD,垂足为E.
在Rt△BAD中,tan B==.
可设AD=5x,则AB=3x.
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴===,
∴CE=x,DE=x,
∴AE=AD+DE=x,
∴在Rt△AEC中,tan∠CAD==.
故答案为.
母题4 A 提示:如图,连接BC.
∵AB是直径,∴∠ACB=90°.
∵☉O的半径为3,∴AB=6,
∴BC===4,
∴tan D=tan A===2.
故选A.
变式练4 解:如图,作AD⊥BC于点D.
∵AB=AC=5,BC=8,
∴BD=CD=4,∠BAD=∠BAC.
∵∠ADB=90°,∴sin∠BAD==.
又∵∠BPC=∠BAC,
∴∠BPC=∠BAD,
∴sin∠BPC=.
母题5 2 提示:如图,过点Q作QC∥BA,连接PC,
∴∠QMB=∠CQP.
由题意得CQ2=22+22=8,
PC2=42+42=32,
PQ2=22+62=40,
∴PC2+CQ2=PQ2,
∴△PCQ是直角三角形,
∴∠PCQ=90°,
∴tan∠CQP===2,
∴tan∠QMB=tan∠CQP=2.
故答案为2.
变式练5 D 提示:如图,延长AC到点D,连接BE交CD于点O,
∴BE⊥CD,AB==,OB=BE==,
∴sin∠BAC===.
故选D.
母题6 提示:∵在△ABC中,∠ACB=90°,AC=BC=4,
∴∠A=∠B.
由折叠的性质得到△AEF≌△DEF,
∴∠EDF=∠A,
∴∠EDF=∠B,
∴∠CDE+∠BDF+∠EDF=∠BFD+∠BDF+∠B=180°,
∴∠CDE=∠BFD.
又∵AE=DE=3,
∴CE=4-3=1.
在直角△ECD中,sin∠CDE==,
∴sin∠BFD=.
故答案为.
变式练6 B 提示:根据题意,BE=AE.设BE=x,则CE=8-x.
在Rt△BCE中,x2=(8-x)2+42,
解得x=5,
∴CE=8-5=3,
∴tan∠CBE==.
故选B.
母题7 D 提示:∵sin A==,
∴设BC=3x,AB=5x.
又∵AC2+BC2=AB2,
∴82+(3x)2=(5x)2,
解得x=2或x=-2(舍去),
∴BC=3x=6 cm.
故选D.
变式练7 B 提示:∵sin2A+cos2A=1,
∴cos A==.
故选B.
母题8 8或24 提示:如图1所示,
∵BC=6,BD∶CD=2∶1,
∴BD=4.
∵AD⊥BC,tan B=,
∴=,
∴AD=BD=,
∴S△ABC=BC AD=×6×=8.
如图2所示,
∵BC=6,BD∶CD=2∶1,∴BD=12.
∵AD⊥BC,tan B=,∴=,∴AD=BD=8,
∴S△ABC=BC AD=×6×8=24.
综上所述,△ABC面积的所有可能值为8或24.
故答案为8或24.
图1 图2
变式练8 3+3或3-3 提示:①当△ABC为锐角三角形时,
过点A作AD⊥BC于点D,如图1.
图1
∵AB=3,∠B=45°,
∴AD=BD=AB·sin 45°=3,
∴CD==3,∴BC=BD+CD=3+3.
②当△ABC为钝角三角形时,
过点A作AD⊥BC交BC延长线于点D,如图2.
图2
∵AB=3,∠B=45°,
∴AD=BD=AB·sin 45°=3,
∴CD==3,
∴BC=BD-CD=3-3.
综上,BC的长为3+3或3-3.
故答案为3+3或3-3.
母题9 解:==.理由如下:如图,过点A作AD⊥BC,过点B作BE⊥AC,
在Rt△ABD中,sin B=,即AD=csin B,
在Rt△ADC中,sin C=,即AD=bsin C,
∴csin B=bsin C,即=,
同理可得=,
则==.
变式练9 解:(1)1;1;1 提示:sin2A1+cos2A1=2+2=+=1,
sin2A2+cos2A2=2+2=+=1,
sin2A3+cos2A3=2+2=+=1.故答案为1;1;1.
(2)1.
(3)在题图2中,∵sin A=,cos A=,且a2+b2=c2,
则sin2A+cos2A=2+2=+===1,
即sin2A+cos2A=1.
(4)在△ABC中,∠A+∠B=90°,∴∠C=90°.
∵sin2A+cos2A=1,∴2+cos2A=1,
解得cos A=或cos A=-(舍去),∴cos A=.
