29.1 投影 同步培优训练(含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 29.1 投影 同步培优训练(含答案)2024-2025学年数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 150.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 11:23:11 | ||
图片预览


文档简介
29.1 投影
任务一 与平行投影有关的计算
母题1 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,木杆EF的长为2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
变式练1:如图,在阳光下,小亮利用所学的数学知识测量某竹竿AB的高度,已知小亮的身高为1.72 m,在同一时刻测得小亮和竹竿AB的投影长分别为0.86 m和6m,求竹竿AB的高.
任务二 与中心投影有关的计算
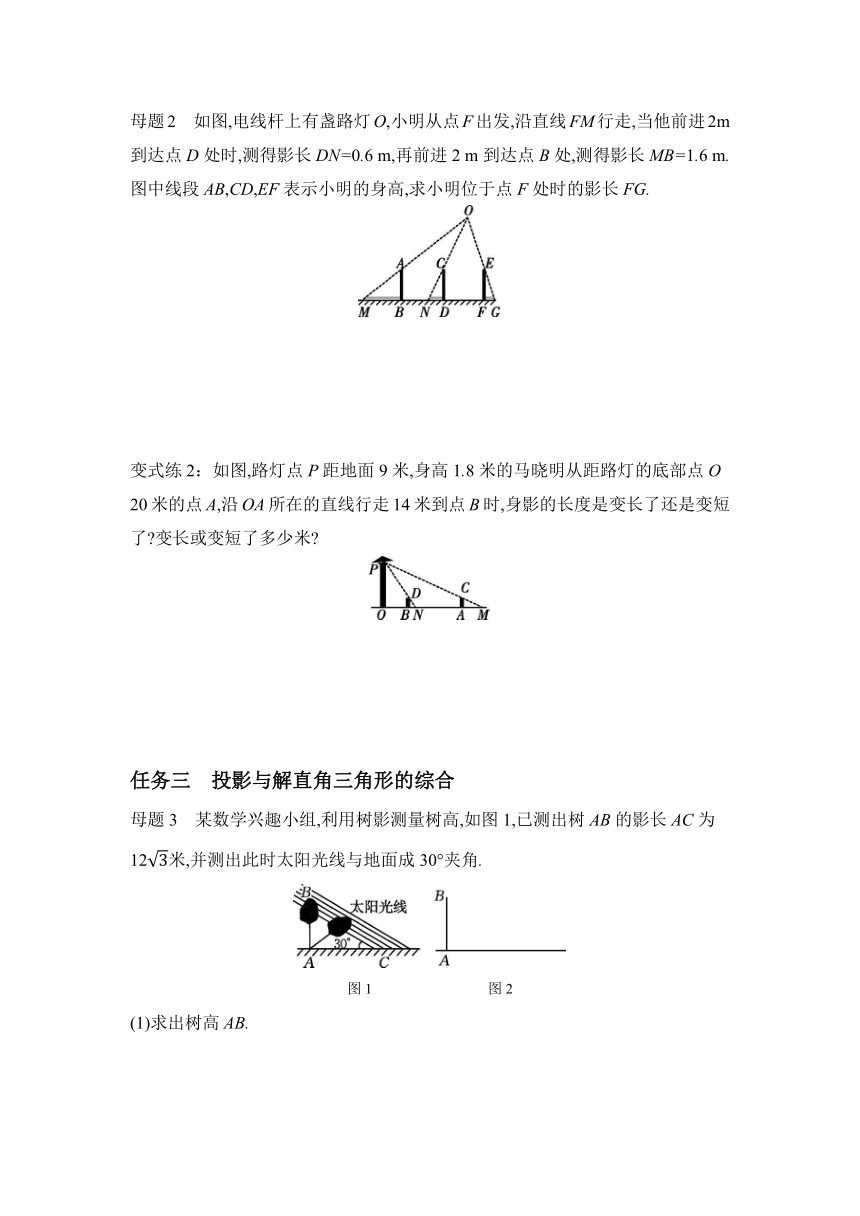
母题2 如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM行走,当他前进2m到达点D处时,测得影长DN=0.6 m,再前进2 m到达点B处,测得影长MB=1.6 m.图中线段AB,CD,EF表示小明的身高,求小明位于点F处时的影长FG.
变式练2:如图,路灯点P距地面9米,身高1.8米的马晓明从距路灯的底部点O
20米的点A,沿OA所在的直线行走14米到点B时,身影的长度是变长了还是变短了 变长或变短了多少米
任务三 投影与解直角三角形的综合
母题3 某数学兴趣小组,利用树影测量树高,如图1,已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
图1 图2
(1)求出树高AB.
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,求树与地面成45°角时的影长.【用图2解答,结果保留根号】
变式练3:如图,太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是10 cm,则皮球的直径是 .
任务四 投影问题的综合应用
母题4 如图,有一根路灯杆AB,在光线下小明在点D处的影长DE=3 m,沿BD方向行走到达点G处,测得DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯杆AB的高度.(结果精确到0.1 m)
变式练4:如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
参考答案
母题1 解:∵BF∥ED,
∴∠BAO=∠EDF.
又∵∠AOB=∠DFE=90°,
∴△ABO∽△DEF.
∴=,
即=,
解得BO=134,
即金字塔的高度BO为134 m.
变式练1 解:由平行投影的性质,可知△DEF∽△ABC,
∴=,
即=,
解得AB=12,
因此竹竿AB的高为12 m.
母题2 解:如图,过点O作OH⊥MG于点H,设DH=x m,
由AB∥CD∥OH,得△ABM∽△OHM,△CDN∽△OHN,
∴=,=.
∵AB=CD,
∴=,
∴=,
解得x=1.2.
设FG=y m,同理得=,
∴=,
解得y=0.4,
所以小明位于点F处时的影长FG为0.4 m.
变式练2 解:∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP,
∴=,
即=,
解得MA=5.
同理,由△NBD∽△NOP,
可求得NB=1.5,
则马晓明的身影变短了5-1.5=3.5(米).
母题3 解:(1)AB=ACtan 30°=12×=12(米).
答:树高约为12米.
(2)如图,B1N=AN=AB1sin 45°=12×=6(米),
NC1=NB1tan 60°=6×=6(米),
AC1=AN+NC1=(6+6)米.
变式练3 解:如图,∵由题意得DC=2R,DE=10,∠CED=60°,
∴DC=DEsin 60°=15(cm).
故答案为15 cm.
母题4 解:由题意,得CD∥AB,
∴△CDE∽△ABE,
∴=,
即=①.
同理,△FGH∽△ABH,
∴=,
即=②.
联立①②,解得BD=7.5,AB=5.95≈6.0.
答:路灯杆AB的高度6.0米.
变式练4 解:如图,过点C作CE⊥AB于点E,过点B作BF⊥CD于点F,
在Rt△BFD中,
∵∠DBF=30°,
∴sin∠DBF==,cos∠DBF==.
∵BD=6,
∴DF=3,BF=3.
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=3,CF=BE=CD-DF=1.
在Rt△ACE中,∠ACE=45°,
∴AE=CE=3,
∴AB=(3+1)米.
答:铁塔AB的高为(3+1)米.
任务一 与平行投影有关的计算
母题1 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,木杆EF的长为2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
变式练1:如图,在阳光下,小亮利用所学的数学知识测量某竹竿AB的高度,已知小亮的身高为1.72 m,在同一时刻测得小亮和竹竿AB的投影长分别为0.86 m和6m,求竹竿AB的高.
任务二 与中心投影有关的计算
母题2 如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM行走,当他前进2m到达点D处时,测得影长DN=0.6 m,再前进2 m到达点B处,测得影长MB=1.6 m.图中线段AB,CD,EF表示小明的身高,求小明位于点F处时的影长FG.
变式练2:如图,路灯点P距地面9米,身高1.8米的马晓明从距路灯的底部点O
20米的点A,沿OA所在的直线行走14米到点B时,身影的长度是变长了还是变短了 变长或变短了多少米
任务三 投影与解直角三角形的综合
母题3 某数学兴趣小组,利用树影测量树高,如图1,已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
图1 图2
(1)求出树高AB.
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,求树与地面成45°角时的影长.【用图2解答,结果保留根号】
变式练3:如图,太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是10 cm,则皮球的直径是 .
任务四 投影问题的综合应用
母题4 如图,有一根路灯杆AB,在光线下小明在点D处的影长DE=3 m,沿BD方向行走到达点G处,测得DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯杆AB的高度.(结果精确到0.1 m)
变式练4:如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
参考答案
母题1 解:∵BF∥ED,
∴∠BAO=∠EDF.
又∵∠AOB=∠DFE=90°,
∴△ABO∽△DEF.
∴=,
即=,
解得BO=134,
即金字塔的高度BO为134 m.
变式练1 解:由平行投影的性质,可知△DEF∽△ABC,
∴=,
即=,
解得AB=12,
因此竹竿AB的高为12 m.
母题2 解:如图,过点O作OH⊥MG于点H,设DH=x m,
由AB∥CD∥OH,得△ABM∽△OHM,△CDN∽△OHN,
∴=,=.
∵AB=CD,
∴=,
∴=,
解得x=1.2.
设FG=y m,同理得=,
∴=,
解得y=0.4,
所以小明位于点F处时的影长FG为0.4 m.
变式练2 解:∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP,
∴=,
即=,
解得MA=5.
同理,由△NBD∽△NOP,
可求得NB=1.5,
则马晓明的身影变短了5-1.5=3.5(米).
母题3 解:(1)AB=ACtan 30°=12×=12(米).
答:树高约为12米.
(2)如图,B1N=AN=AB1sin 45°=12×=6(米),
NC1=NB1tan 60°=6×=6(米),
AC1=AN+NC1=(6+6)米.
变式练3 解:如图,∵由题意得DC=2R,DE=10,∠CED=60°,
∴DC=DEsin 60°=15(cm).
故答案为15 cm.
母题4 解:由题意,得CD∥AB,
∴△CDE∽△ABE,
∴=,
即=①.
同理,△FGH∽△ABH,
∴=,
即=②.
联立①②,解得BD=7.5,AB=5.95≈6.0.
答:路灯杆AB的高度6.0米.
变式练4 解:如图,过点C作CE⊥AB于点E,过点B作BF⊥CD于点F,
在Rt△BFD中,
∵∠DBF=30°,
∴sin∠DBF==,cos∠DBF==.
∵BD=6,
∴DF=3,BF=3.
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=3,CF=BE=CD-DF=1.
在Rt△ACE中,∠ACE=45°,
∴AE=CE=3,
∴AB=(3+1)米.
答:铁塔AB的高为(3+1)米.
