上海市华东师大二附中2016届高三(上)期中数学试卷(解析版)
文档属性
| 名称 | 上海市华东师大二附中2016届高三(上)期中数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-24 00:00:00 | ||
图片预览




文档简介
2015-2016学年上海市华东师大二附中高三(上)期中数学试卷
一、填空题(本题满分56分)本大题共有14题,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.已知全集U=R,集合,则 UM= .
2.设z1=1﹣i,z2=a+2ai(a∈R),其中i 是虚数单位,若复数z1+z2 是纯虚数,则a= .
3.经过圆(x﹣1)2+y2=1的圆心M,且与直线x﹣y=0垂直的直线方程是 .
4.△ABC中,a,b,c分别是角A,B,C的对边,,则A= .
5.已知数列{an}是等差数列,且a1+a7+a13=2π,则tan(a2+a12)═ .
6.若命题“ x∈R,使得x2+(a﹣1)x+1<0”是真命题,则实数a的取值范围是 .
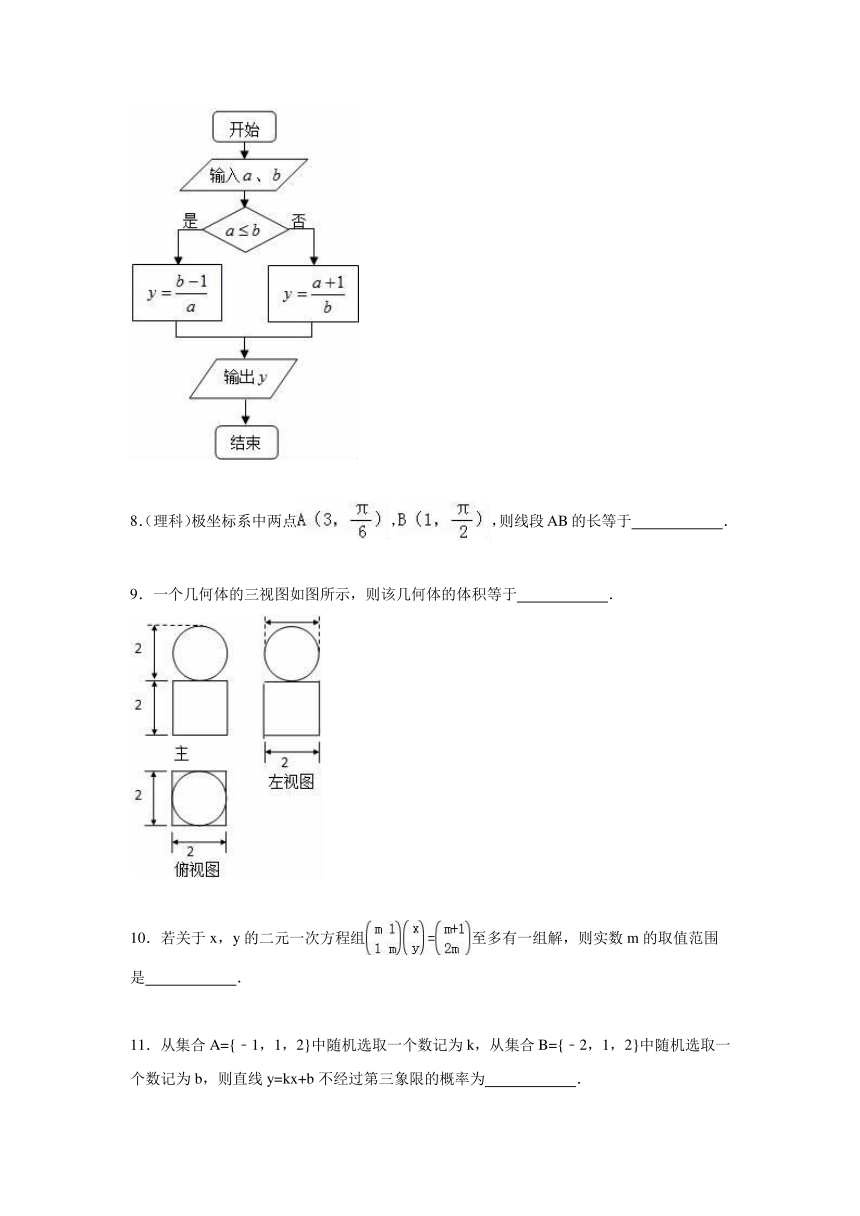
7.对任意非零实数a、b,定义一种运算:a b,其结果y=a b的值由如图确定,则= .
8.(理科)极坐标系中两点,,则线段AB的长等于 .
9.一个几何体的三视图如图所示,则该几何体的体积等于 .
10.若关于x,y的二元一次方程组至多有一组解,则实数m的取值范围是 .
11.从集合A={﹣1,1,2}中随机选取一个数记为k,从集合B={﹣2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第三象限的概率为 .
12.不等式sin2x+acosx+a2≥1+cosx对一切x∈R成立,则实数a的取值范围为 .
13.如图已知每条棱长都为3的直平行六面体ABCD﹣A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为 .
14.在平面直角坐标系中,定义(n∈N*为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么的值为= .
15.若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:
①τ={ ,{a},{c},{a,b,c}};
②τ={ ,{b},{c},{b,c},{a,b,c}};
③τ={ ,{a},{a,b},{a,c}};
④τ={ ,{a,c},{b,c},{c},{a,b,c}}.
其中是集合X上的拓扑的集合τ的序号是 .
二、选择题(本题满分16分)本大题共有5题,每题都给出四个结论,其中有且只有一个结论是正确的选对得4分,否则一律得零分.
16.A,B两点在半径为2的球面上,且以线段AB为直径的小圆周长为2π,则A,B两点间的球面距离为( )
A.π B.2π C. D.
17.已知函数,则“f(2)<f(3)”是“f(x)在区间(﹣2,+∞)上单调递增”的什么条件.( )
A.“充要” B.“充分不必要”
C.“必要不充分” D.“既不充分也不必要”
18.设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④M中所有直线均经过一个定点;
⑤不存在定点P不在M中的任一条直线上;
⑥对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上;
⑦M中的直线所能围成的正三角形面积都相等.
A.3 B.4 C.5 D.6
19.(2015秋 上海校级期中)在约束条件下,若3≤S≤5,则目标函数z=3x+2y的最大值变化范围是( )
A.[6,8] B.[6,15] C.[7,8] D.[7,15]
20.长度分别为2、x、x、x、x、x的六条线段能成为同一个四面体的六条棱的充要条件是( )
A.x B. C. D.x>1
三、解答题
21.关于x的不等式<0的解集为(﹣1,b).
(1)求实数a、b的值;
(2)若z1=a+bi,z2=cosα+isinα,且z1z2为纯虚数,求的值.
22.如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为,求k的值
(3)现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
23.如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(﹣,C,内切圆圆心I(1,t).设A点的轨迹为L
(1)求L的方程;
(2)过点C作直线m交曲线L于不同的两点M、N,问在x轴上是否存在一个异于点C的定点Q.使对任意的直线m都成立?若存在,求出Q的坐标,若不存在,说明理由.
24.设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件,试求Sn的最大值.
25.已知f(x)=.
(1)求f(f(x));
(2)对参数a的哪些值,方程|x|+||=a正好有3个实数解;
(3)设b为任意实数,证明:x+﹣=b共有3个不同的实数解x1,x2,x3,并且x1+x2+x3=b.
2015-2016学年上海市华东师大二附中高三(上)期中数学试卷
参考答案与试题解析
一、填空题(本题满分56分)本大题共有14题,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.已知全集U=R,集合,则 UM= {x|x<1} .
【考点】函数的定义域及其求法;补集及其运算.
【专题】计算题.
【分析】由题意全集U=R,再根据函数的定义域写出集合M,然后根据交集的定义和运算法则进行计算即可.
【解答】解:因为集合M={x|x﹣1≥0}={x|x≥1},
全集U=R,
∴CUM={x|x<1}.
故答案为:{x|x<1}.
【点评】本题考查集合的补集运算和求函数的定义域,属容易题.
2.设z1=1﹣i,z2=a+2ai(a∈R),其中i 是虚数单位,若复数z1+z2 是纯虚数,则a= ﹣1 .
【考点】复数的基本概念.
【专题】计算题.
【分析】首先把两个复数相加,实部和虚部分别相加,得到复数的标准形式,根据所给的复数是一个纯虚数,得到实部等于0,虚部不等于0,解出结果.
【解答】解:∵z1=1﹣i,z2=a+2ai,
∴z1+z2=a+1+(2a﹣1)i,
∵复数z1+z2 是纯虚数,
∴a+1=0,2a﹣1≠0,
∴a=﹣1,
故答案为:﹣1.
【点评】本题考查复数的基本概念和加减运算,是一个基础题,解题的关键是看清题目中的要求,注意一定要上虚部不等于0.
3.经过圆(x﹣1)2+y2=1的圆心M,且与直线x﹣y=0垂直的直线方程是 x+y﹣1=0 .
【考点】圆的切线方程.
【专题】计算题;方程思想;综合法;圆锥曲线的定义、性质与方程.
【分析】易得圆心坐标,由垂直关系可得直线的斜率,可得点斜式方程,化为一般式即可.
【解答】解:圆(x﹣1)2+y2=1的圆心M为(1,0),
又直线x﹣y=0的斜率为1,
由垂直关系可得要求直线的斜率为﹣1,
∴直线方程为y﹣0=﹣(x﹣1),即x+y﹣1=0.
故答案为:x+y﹣1=0.
【点评】本题考查直线的一般式方程和垂直关系,涉及圆的标准方程,属基础题.
4.△ABC中,a,b,c分别是角A,B,C的对边,,则A= 45° .
【考点】正弦定理.
【专题】计算题.
【分析】由a,b及sinB的值,利用正弦定理求出sinA的值,再由a小于b,利用三角形中大边对大角得到A小于B,确定出A的范围,进而由sinA的值,利用特殊角的三角函数值即可求出A的度数.
【解答】解:∵a=,b=,B=60°,
∴由正弦定理=得:sinA==,
又<,即a<b,∴A<B,
则A=45°.
故答案为:45°
【点评】此题考查了正弦定理,三角形的边角关系,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.
5.已知数列{an}是等差数列,且a1+a7+a13=2π,则tan(a2+a12)═ .
【考点】等差数列的性质.
【专题】等差数列与等比数列.
【分析】由等差数列的性质易得a7=,进而可得tan(a2+a12)=tan(2a7),代值计算可得.
【解答】解:由等差数列的性质可得a1+a7+a13=3a7=2π,∴a7=,
∴tan(a2+a12)=tan(2a7)=tan=
故答案为:
【点评】本题考查等差数列的性质,涉及正切的运算,属基础题.
6.若命题“ x∈R,使得x2+(a﹣1)x+1<0”是真命题,则实数a的取值范围是 (﹣∞,﹣1)∪(3,+∞) .
【考点】二次函数的性质.
【专题】计算题.
【分析】因为不等式对应的是二次函数,其开口向上,若“ x∈R,使得x2+(a﹣1)x+1<0”,则相应二次方程有不等的实根.
【解答】解:∵“ x∈R,使得x2+(a﹣1)x+1<0
∴x2+(a﹣1)x+1=0有两个不等实根
∴△=(a﹣1)2﹣4>0
∴a<﹣1或a>3
故答案为:(﹣∞,﹣1)∪(3,+∞)
【点评】本题主要考查一元二次不等式,二次函数,二次方程间的相互转化及相互应用,这是在函数中考查频率较高的题目,灵活多变,难度可大可小,是研究函数的重要方面.
7.对任意非零实数a、b,定义一种运算:a b,其结果y=a b的值由如图确定,则= 1 .
【考点】程序框图.
【专题】计算题;图表型;分类讨论;算法和程序框图.
【分析】通过程序框图判断出新运算S=a b的解析式,化简,再利用新运算法则求出值.
【解答】解:由程序框图知 S=a b=,
∴=3 4==1
故答案为:1.
【点评】本题考查判断程序框图的功能即判断出新运算法则.利用运算法则求值,属于基础题.
8.(理科)极坐标系中两点,,则线段AB的长等于 .
【考点】由三视图求面积、体积.
【专题】数形结合;定义法;坐标系和参数方程.
【分析】根据极坐标系中两点间的距离公式,求出线段AB的长即可.
【解答】解:极坐标系中,,
∴线段AB的长为
|AB|==.
故答案为:.
【点评】本题考查了极坐标系中两点间的距离公式的应用问题,是基础题目.
9.一个几何体的三视图如图所示,则该几何体的体积等于 .
【考点】由三视图求面积、体积.
【专题】计算题.
【分析】由三视图知,原几何体是一个球和一个正方体构成的组合体,再根据三视图得到球的半径和正方体的棱长,即可求体积
【解答】解:由三视图知原几何体是一个球和一个正方体构成的组合体,球的直径为2,半径为1,正方体的棱长为2
∴原几何体的体积为:
故答案为:
【点评】本题考查三视图,要求能把三视图还原成原几何体,能根据三视图找到原几何体的长度关系,要求有较好的空间想象力.属简单题
10.若关于x,y的二元一次方程组至多有一组解,则实数m的取值范围是 (﹣∞,1)∪(1,+∞) .
【考点】系数矩阵的逆矩阵解方程组;二元一次方程组的矩阵形式.
【专题】计算题.
【分析】先根据矩阵的乘法进行化简得到二元一次方程组,然后消去y得(m2﹣1)x=m(m﹣1),当m﹣1≠0时(m2﹣1)x=m(m﹣1)至多有一组解,从而求出m的范围.
【解答】解:关于x,y的二元一次方程组
即二元一次方程组
①×m﹣②得(m2﹣1)x=m(m﹣1)
当m﹣1≠0时(m2﹣1)x=m(m﹣1)至多有一组解
∴m≠1
故答案为:(﹣∞,1)∪(1,+∞)
【点评】本题主要考查了二元一次方程组的解的个数,以及矩阵的乘法运算,属于中档题.
11.从集合A={﹣1,1,2}中随机选取一个数记为k,从集合B={﹣2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第三象限的概率为 .
【考点】古典概型及其概率计算公式.
【专题】计算题;概率与统计.
【分析】本题是一个古典概型,试验发生包含的事件(k,b)的取值所有可能的结果可以列举出,满足条件的事件直线不经过第三象限,符合条件的(k,b)有2种结果,根据古典概型概率公式得到结果.
【解答】解:由题意知本题是一个古典概型,试验发生包含的事件k∈A={﹣1,1,2},b∈B={﹣2,1,2},
得到(k,b)的取值所有可能的结果有:(﹣1,﹣2);(﹣1,1);(﹣1,2);(1,﹣2);(1,1);(1,2);
(2,﹣2);(2,1);(2,2)共9种结果.
而当时,直线不经过第三象限,符合条件的(k,b)有2种结果,
∴直线不过第四象限的概率P=,
故答案为.
【点评】古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、体积的比值得到,属于基础题.
12.不等式sin2x+acosx+a2≥1+cosx对一切x∈R成立,则实数a的取值范围为 a≥1或a≤﹣2 .
【考点】三角函数的最值;三角函数中的恒等变换应用.
【专题】函数的性质及应用;三角函数的图像与性质.
【分析】不等式进行等价转化为关于cosx的一元二次不等式,利用二次函数的性质和图象列不等式组求得答案.
【解答】解;不等式等价于1﹣cos2x+acosx+a2﹣1﹣cosx≥0,恒成立,
整理得﹣cos2x+(a﹣1)cosx+a2≥0,
设cosx=t,则﹣1≤t≤1,
g(t)=﹣t2+(a﹣1)t+a2,要使不等式恒成立需
,求得a≥1或a≤﹣2,
故答案为:a≥1或a≤﹣2.
【点评】本题主要考查了一元二次不等式的解法,二次函数的性质.注重了对数形结合思想的运用和问题的分析.
13.如图已知每条棱长都为3的直平行六面体ABCD﹣A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为 .
【考点】棱柱、棱锥、棱台的体积;棱柱的结构特征.
【专题】计算题.
【分析】先推导点P的轨迹,从而确定点P与平行六面体所围成的几何体的形状,然后求几何体的体积
【解答】解:取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
以DE所在直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立如图空间直角坐标系
设M(0,0,z),N(x,y,0),则P()
MN=
∴x2+y2+z2=4
∴
∴OP2=1
即OP=1
∴点P的轨迹是以原点D为球心,以1为半径的球的一部分
又∵∠BAD=60°
∴∠ADC=120°
∴点P的轨迹是球的
∴几何体的体积为
故答案为:
【点评】本题考查几何体的体积,须先用代数法确定点的轨迹,然后熟练应用体积公式即可.属中档题
14.在平面直角坐标系中,定义(n∈N*为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么的值为= 2+ .
【考点】数列的极限.
【专题】新定义;转化思想;分析法;等差数列与等比数列.
【分析】由题设知a1=|(0,1) (1,1)|=1,a2=|(1,1) (0,2)|=,a3=|(0,2) (2,2)|=2,a4=|(2,2) (0,4)|=2,…,an=()n﹣1,Sn=a1+a2+a3+…+an=.由此可求出的值.
【解答】解:由题设知P1(0,1),P2(1,1),a1=|P1P2|=1,
且当n≥2时,an2=|PnPn+1|2=(xn+1﹣xn)2﹣(yn+1﹣yn)2
=[(yn﹣xn)﹣xn]2+[(yn+xn)﹣yn]2=5xn2﹣4xnyn+yn2
an﹣12=|Pn﹣1Pn|2=(xn﹣xn﹣1)2﹣(yn﹣yn﹣1)2①
由定义(n∈N),得,
∴,
代入①计算化简得an﹣12=|Pn﹣1Pn|2=()2+()2=(5xn2﹣4xnyn+yn2)=an2.
∴=(n≥2),
∴数列{an}是以为公比的等比数列,且首项a1=1,
∴an=()n﹣1,
∴Sn=a1+a2+a3+…+an=.
∴= =,
则===2+.
故答案为:.
【点评】本题考查集合的性质和运算,解题时要注意等比数列前n项和公式的合理运用,属于中档题.
15.若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:
①τ={ ,{a},{c},{a,b,c}};
②τ={ ,{b},{c},{b,c},{a,b,c}};
③τ={ ,{a},{a,b},{a,c}};
④τ={ ,{a,c},{b,c},{c},{a,b,c}}.
其中是集合X上的拓扑的集合τ的序号是 ②④ .
【考点】集合的包含关系判断及应用.
【专题】压轴题;新定义.
【分析】根据集合X上的拓扑的集合τ的定义,逐个验证即可:①{a}∪{c}={a,c} τ,③{a,b}∪{a,c}={a,b,c} τ,因此①③都不是;
②④满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ,因此②④是,从而得到答案.
【解答】解:①τ={ ,{a},{c},{a,b,c}};
而{a}∪{c}={a,c} τ,故①不是集合X上的拓扑的集合τ;
②τ={ ,{b},{c},{b,c},{a,b,c}},满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ
因此②是集合X上的拓扑的集合τ;
③τ={ ,{a},{a,b},{a,c}};
而{a,b}∪{a,c}={a,b,c} τ,故③不是集合X上的拓扑的集合τ;
④τ={ ,{a,c},{b,c},{c},{a,b,c}}.
满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ
因此④是集合X上的拓扑的集合τ;
故答案为②④.
【点评】此题是基础题.这是考查学生理解能力和对知识掌握的灵活程度的问题,重在理解题意.本题是开放型的问题,要认真分析条件,探求结论,对分析问题解决问题的能力要求较高.
二、选择题(本题满分16分)本大题共有5题,每题都给出四个结论,其中有且只有一个结论是正确的选对得4分,否则一律得零分.
16.A,B两点在半径为2的球面上,且以线段AB为直径的小圆周长为2π,则A,B两点间的球面距离为( )
A.π B.2π C. D.
【考点】多面体和旋转体表面上的最短距离问题.
【专题】数形结合;数形结合法;立体几何.
【分析】求出球的半径,利用等边三角形求出∠AOB的大小,再求球面距离弧AB.
【解答】解:根据题意画出示意图,如图所示:
∵球的半径为R=2,且以线段AB为直径的小圆周长为2π,
∴小圆直径为AB=2;
∴在三角形AOB中,AO=AB=BO=2,
∴∠AOB=,
∴A,B两点间的球面距离为:l=R=.
故选:D.
【点评】本题考查了球面距离的应用问题,也考查了圆的周长与弧长的计算问题,是基础题目.
17.已知函数,则“f(2)<f(3)”是“f(x)在区间(﹣2,+∞)上单调递增”的什么条件.( )
A.“充要” B.“充分不必要”
C.“必要不充分” D.“既不充分也不必要”
【考点】必要条件、充分条件与充要条件的判断.
【专题】函数思想;综合法;圆锥曲线的定义、性质与方程.
【分析】先求出函数f(x)的导数,求出“f(x)在区间(﹣2,+∞)上单调递增”的充要条件,从而得到答案.
【解答】解:f′(x)==,
如f(x)在区间(﹣2,+∞)上单调递增,
则2a﹣1>0,解得:a>,
由f(2)<f(3),得:<,解得:a>,
故f(2)<f(3)”是“f(x)在区间(﹣2,+∞)上单调递增”的充要条件,
故选:A.
【点评】本题考查了充分必要条件,考查函数的单调性问题,是一道基础题.
18.设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④M中所有直线均经过一个定点;
⑤不存在定点P不在M中的任一条直线上;
⑥对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上;
⑦M中的直线所能围成的正三角形面积都相等.
A.3 B.4 C.5 D.6
【考点】直线的斜截式方程.
【分析】根据已知可知直线系M都为以(0,2)为圆心,以1为半径的圆的切线,取半径为2即可得到所以①对;存在圆心为(0,2),半径为的圆与直线都不相交,所以②对;③显然对;④错;⑤错,存在可取一点(0,2)即可验证;⑥可去三角形的外接正三角形所有边均在M中的直线上且面积相等,所以⑥都正确.⑦可以举反例.
【解答】解:根据直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π)得到所有直线都为圆心为(0,2),半径为1的圆的切线;
可取圆心为(0,2),半径分别为2,,1得到①②③正确;所有的直线与一个圆相切,没有过定点,④错;存在(0,2)不在M中的任一条直线上,所以⑤错;存在等边三角形的三边都在M中的直线上,⑥对,可取圆的外接正三角形其所有边均在M中的直线上且面积相等;⑦可以做在圆的三等分点做圆的切线,把其中一条平移到另外两个点中点时,可知⑦错误;故①②③⑥正确,④⑤⑦错,所以真命题的个数为4个
故选:B
【点评】考查学生利用直线的斜截式方程得到直线系M为平面内除过一个圆的区域.
19.(2015秋 上海校级期中)在约束条件下,若3≤S≤5,则目标函数z=3x+2y的最大值变化范围是( )
A.[6,8] B.[6,15] C.[7,8] D.[7,15]
【考点】简单线性规划.
【专题】不等式的解法及应用.
【分析】先根据约束条件画出可行域,设z=3x+2y,再利用z的几何意义求最值,只需求出直线z=3x+2y过可行域内的点时,从而得到z=3x+2y的最大值即可.
【解答】解:先根据约束条件画出可行域,
设z=3x+2y,
将z的值转化为直线z=3x+2y在y轴上的截距,
当S=3时,对应的平面区域为四边形OCAD,
当直线z=3x+2y经过点A(1,2)时,z最大,最大值为7.
当S=5时,对应的平面区域为三角形OBD,
当直线z=3x+2y经过点B(0,4)时,z最大,最大值为8,
故当3≤S≤5时,目标函数z=3x+2y的最大值的变化范围是[7,8].
故选:C
【点评】本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,利用数形结合是解决本题的关键.
20.长度分别为2、x、x、x、x、x的六条线段能成为同一个四面体的六条棱的充要条件是( )
A.x B. C. D.x>1
【考点】棱锥的结构特征.
【专题】压轴题;探究型.
【分析】用极限的角度考虑,可求x接近最小的数值,得不到最大值,求出结果.
【解答】解:用极限的角度考虑,四面体趋近于在一个平面内的菱形时x最小,
不能低于,最大可以无穷大(就是两个等边三角形的二面角可以无限趋于0),
【点评】本题考查棱锥的结构特征,考查空间想象能力,极限思想的应用,是中档题.
三、解答题
21.关于x的不等式<0的解集为(﹣1,b).
(1)求实数a、b的值;
(2)若z1=a+bi,z2=cosα+isinα,且z1z2为纯虚数,求的值.
【考点】二阶矩阵;两角和与差的余弦函数.
【专题】计算题.
【分析】(1)将原不等式转化为(x+a)x﹣2<0,即x2+ax﹣2<0,根据解集为(﹣1,b)得到﹣1,b是方程x2+ax﹣2=0的两个根,结合根与系数的关系即可列出关于a,b的方程组,并利用解二元一次方程组的方法即可求解
(2)根据z1z2为纯虚数,得知实部为0,虚部不为0,即可得到关于α的条件式并解得:tanα=﹣,再利用两角差的余弦,倍角公式和同角的三角关系将化为关于tanα的代数式即可求解
【解答】解:(1)原不等式等价于(x+a)x﹣2<0,
即x2+ax﹣2<0
由题意得,
解得a=﹣1,b=2.
(2)z1=﹣1+2i,z1z2=(﹣cosα﹣2sinα)+i(2cosα﹣sinα)
若z1z2为纯虚数,则,
解得
==.
【点评】本题考查了二阶矩阵,两角和与差的余弦函数及解三角方程的能力,属于基础题.
22.如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为,求k的值
(3)现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
【考点】用空间向量求直线与平面的夹角;棱柱、棱锥、棱台的侧面积和表面积;直线与平面垂直的判定;直线与平面所成的角.
【专题】压轴题;空间位置关系与距离;空间角.
【分析】(1)取DC得中点E,连接BE,可证明四边形ABED是平行四边形,再利用勾股定理的逆定理可得BE⊥CD,即CD⊥AD,又侧棱AA1⊥底面ABCD,可得AA1⊥DC,利用线面垂直的判定定理即可证明.(2)通过建立空间直角坐标系,求出平面的法向量与斜线的方向向量的夹角即可得出;(3)由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案
新四棱柱共有此4种不同方案.写出每一方案下的表面积,通过比较即可得出f(k).
【解答】(1)证明:取DC的中点E,连接BE,∵AB∥ED,AB=ED=3k,
∴四边形ABED是平行四边形,
∴BE∥AD,且BE=AD=4k,∴BE2+EC2=(4k)2+(3k)2=(5k)2=BC2,∴∠BEC=90°,∴BE⊥CD,
又∵BE∥AD,∴CD⊥AD.
∵侧棱AA1⊥底面ABCD,∴AA1⊥CD,
∵AA1∩AD=A,∴CD⊥平面ADD1A1.
(2)解:以D为坐标原点,、、的方向为x,y,z轴的正方向建立空间直角坐标系,
则A(4k,0,0),C(0,6k,0),B1(4k,3k,1),A1(4k,0,1).
∴,,.
设平面AB1C的一个法向量为=(x,y,z),则,取y=2,则z=﹣6k,x=3.∴.
设AA1与平面AB1C所成角为θ,则===,解得k=1,故所求k=1.
(3)由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案新四棱柱共有此4种不同方案.
写出每一方案下的表面积,通过比较即可得出f(k)=
【点评】本题主要考查了线线、线面的位置关系、通过建立空间直角坐标系利用法向量求线面角、柱体的定义积表面积、勾股定理的逆定理等基础知识,考查了空间想象能力、推理能力和计算能力及化归与转化能力.
23.如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(﹣,C,内切圆圆心I(1,t).设A点的轨迹为L
(1)求L的方程;
(2)过点C作直线m交曲线L于不同的两点M、N,问在x轴上是否存在一个异于点C的定点Q.使对任意的直线m都成立?若存在,求出Q的坐标,若不存在,说明理由.
【考点】轨迹方程;直线与圆锥曲线的关系.
【专题】计算题.
【分析】(1)由切线长定理得,从一点出发的切线长相等,得到A点到两个点B,C的距离之差是常数,根据双曲线的定义得A点的轨迹是双曲线,从而即可求出L的方程;
(2)对于存在性问题,可先假设存在,设点Q(x0,0),再设M(x1,y1),N(x2,y2),由条件得∠MQC=∠NQC,下面分类讨论:①当MN⊥x,②当MN不垂直x时,第一种情况比较简单,对于第二种情况,将直线的方程代入双曲线方程,消去y得到关于x的二次方程,结合根与系数的关系,利用斜率相等求得,从而说明存在点Q.
【解答】解:(1)由题意|AD|=|AF|.|BD|=|BE|,|CE|=|CF|.
∴|AB|﹣|AC|=|BD|﹣|CF|=|BE|﹣|CE|=|BO|+|OE|﹣(|OC|﹣|OE|)=2|OE|
I(1,t),E(1,0),|OE|=1,|AB|﹣|AC|=2
x2﹣y2=1(x>1)
(2)设点Q(x0,0),设M(x1,y1),N(x2,y2)
∵ ∠MQC=∠NQC
于是:①当MN⊥x,点Q(x0,0)在x上任何一点处,都能够使得:
∠MQC=∠NQC成立,
②当MN不垂直x时,设直线.
由得:
则:
∴
∵,要使∠MQC=∠NQC成立,
只要tan∠MQC=tan∠NQC: x2y1﹣x0y1+x1y2﹣x0y2=0
即=
∴ ∴当时,能够使:
对任意的直线m成立.
【点评】本题主要考查了轨迹方程、直线与圆锥曲线的交点等知识,属于中档题.
24.设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件,试求Sn的最大值.
【考点】等差数列与等比数列的综合;数列的求和.
【专题】综合题;等差数列与等比数列.
【分析】(1)设{an}的公差为d,利用裂项法原等式可化为(﹣+﹣+…+﹣)=,整理可得(k﹣1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
(2)当k=1,b=0时,假设p是q的必要条件,分当n=1时,当n≥2时,当n≥3时讨论即可判断结论是否正确;
(3)由+≤M,可设a1=rcosθ,an+1=rsinθ,代入求和公式Sn=,利用三角函数的有界性即可求得其最大值.
【解答】解:(1)设{an}的公差为d,则原等式可化为(﹣+﹣+…+﹣)=,
所以 =,
即(k﹣1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…
(2)当k=1,b=0时,假设p是q的必要条件,即“若++…+=①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
当n=1时, =显然成立.…
当n≥2时,若++…+=②,
由①﹣②得, =(﹣),即nan﹣(n﹣1)an+1=a1③.
当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n﹣1)an﹣1﹣(n﹣2)an=a1④,即2an=an﹣1+an+1.所以{an}为等差数列,即p是q的必要条件.…
(3)由+≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤.
设{an}的公差为d,则an+1﹣a1=nd=rsinθ﹣rcosθ,
所以d=,
所以an=rsinθ﹣,
Sn==r≤ =,
所以Sn的最大值为…
【点评】本题考查等差数列与等比数列的综合,突出考查“充分、必要条件”在数列中的综合应用,判断(2)中“p是否为q的必要条件”是难点,考查参数方程及三角函数的有界性,属于难题.
25.已知f(x)=.
(1)求f(f(x));
(2)对参数a的哪些值,方程|x|+||=a正好有3个实数解;
(3)设b为任意实数,证明:x+﹣=b共有3个不同的实数解x1,x2,x3,并且x1+x2+x3=b.
【考点】根的存在性及根的个数判断;函数的值.
【专题】计算题;作图题;证明题;数形结合;函数的性质及应用.
【分析】(1)化简可得f(f(x))=f()=x,
(2)作函数y=||与函数y=a﹣|x|的图象,从而化为x+=a有一个解,从而利用判别式解得.
(3)化简方程可得x3﹣bx2+(b﹣21)x+2b﹣7=0,从而令g(x)=x3﹣bx2+(b﹣21)x+2b﹣7,从而利用零点的判定定理判断即可.
【解答】解:(1)∵f(x)=,
∴f(f(x))=f()=x,
(2)作函数y=||与函数y=a﹣|x|的图象如下,
若使方程|x|+||=a正好有3个实数解,
则x+=a有一个解,
即3x2﹣3ax+a+1=0有一个解,
故△=9a2﹣12a﹣12=0,
解得,a=2或a=﹣(舍去);
故a=2;
(3)证明:∵x+﹣=b,
∴=b,
∴x3﹣bx2+(b﹣21)x+2b﹣7=0,
令g(x)=x3﹣bx2+(b﹣21)x+2b﹣7,
易知g(x)=﹣∞,g(x)=+∞,
g(﹣1)=﹣1﹣b﹣b+21+2b﹣7=13>0,
g(2)=8﹣4b+2b﹣42+2b﹣7=﹣41<0,
故g(x)在(﹣∞,﹣1),(﹣1,2),(2,+∞)上各有一个零点,
故g(x)有3个不同的零点x1,x2,x3,
故x+﹣=b共有3个不同的实数解x1,x2,x3,
∵x3﹣bx2+(b﹣21)x+2b﹣7=(x﹣x1)(x﹣x2)(x﹣x3)
=x3﹣(x1+x2+x3)x2+(x1x2+x1x3+x3x2)x﹣x1x2x3,
故x1+x2+x3=b.
【点评】本题考查了数形结合的思想应用及分段函数的应用,同时考查了函数的零点与方程的根的关系应用.
一、填空题(本题满分56分)本大题共有14题,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.已知全集U=R,集合,则 UM= .
2.设z1=1﹣i,z2=a+2ai(a∈R),其中i 是虚数单位,若复数z1+z2 是纯虚数,则a= .
3.经过圆(x﹣1)2+y2=1的圆心M,且与直线x﹣y=0垂直的直线方程是 .
4.△ABC中,a,b,c分别是角A,B,C的对边,,则A= .
5.已知数列{an}是等差数列,且a1+a7+a13=2π,则tan(a2+a12)═ .
6.若命题“ x∈R,使得x2+(a﹣1)x+1<0”是真命题,则实数a的取值范围是 .
7.对任意非零实数a、b,定义一种运算:a b,其结果y=a b的值由如图确定,则= .
8.(理科)极坐标系中两点,,则线段AB的长等于 .
9.一个几何体的三视图如图所示,则该几何体的体积等于 .
10.若关于x,y的二元一次方程组至多有一组解,则实数m的取值范围是 .
11.从集合A={﹣1,1,2}中随机选取一个数记为k,从集合B={﹣2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第三象限的概率为 .
12.不等式sin2x+acosx+a2≥1+cosx对一切x∈R成立,则实数a的取值范围为 .
13.如图已知每条棱长都为3的直平行六面体ABCD﹣A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为 .
14.在平面直角坐标系中,定义(n∈N*为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么的值为= .
15.若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:
①τ={ ,{a},{c},{a,b,c}};
②τ={ ,{b},{c},{b,c},{a,b,c}};
③τ={ ,{a},{a,b},{a,c}};
④τ={ ,{a,c},{b,c},{c},{a,b,c}}.
其中是集合X上的拓扑的集合τ的序号是 .
二、选择题(本题满分16分)本大题共有5题,每题都给出四个结论,其中有且只有一个结论是正确的选对得4分,否则一律得零分.
16.A,B两点在半径为2的球面上,且以线段AB为直径的小圆周长为2π,则A,B两点间的球面距离为( )
A.π B.2π C. D.
17.已知函数,则“f(2)<f(3)”是“f(x)在区间(﹣2,+∞)上单调递增”的什么条件.( )
A.“充要” B.“充分不必要”
C.“必要不充分” D.“既不充分也不必要”
18.设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④M中所有直线均经过一个定点;
⑤不存在定点P不在M中的任一条直线上;
⑥对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上;
⑦M中的直线所能围成的正三角形面积都相等.
A.3 B.4 C.5 D.6
19.(2015秋 上海校级期中)在约束条件下,若3≤S≤5,则目标函数z=3x+2y的最大值变化范围是( )
A.[6,8] B.[6,15] C.[7,8] D.[7,15]
20.长度分别为2、x、x、x、x、x的六条线段能成为同一个四面体的六条棱的充要条件是( )
A.x B. C. D.x>1
三、解答题
21.关于x的不等式<0的解集为(﹣1,b).
(1)求实数a、b的值;
(2)若z1=a+bi,z2=cosα+isinα,且z1z2为纯虚数,求的值.
22.如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为,求k的值
(3)现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
23.如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(﹣,C,内切圆圆心I(1,t).设A点的轨迹为L
(1)求L的方程;
(2)过点C作直线m交曲线L于不同的两点M、N,问在x轴上是否存在一个异于点C的定点Q.使对任意的直线m都成立?若存在,求出Q的坐标,若不存在,说明理由.
24.设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件,试求Sn的最大值.
25.已知f(x)=.
(1)求f(f(x));
(2)对参数a的哪些值,方程|x|+||=a正好有3个实数解;
(3)设b为任意实数,证明:x+﹣=b共有3个不同的实数解x1,x2,x3,并且x1+x2+x3=b.
2015-2016学年上海市华东师大二附中高三(上)期中数学试卷
参考答案与试题解析
一、填空题(本题满分56分)本大题共有14题,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.已知全集U=R,集合,则 UM= {x|x<1} .
【考点】函数的定义域及其求法;补集及其运算.
【专题】计算题.
【分析】由题意全集U=R,再根据函数的定义域写出集合M,然后根据交集的定义和运算法则进行计算即可.
【解答】解:因为集合M={x|x﹣1≥0}={x|x≥1},
全集U=R,
∴CUM={x|x<1}.
故答案为:{x|x<1}.
【点评】本题考查集合的补集运算和求函数的定义域,属容易题.
2.设z1=1﹣i,z2=a+2ai(a∈R),其中i 是虚数单位,若复数z1+z2 是纯虚数,则a= ﹣1 .
【考点】复数的基本概念.
【专题】计算题.
【分析】首先把两个复数相加,实部和虚部分别相加,得到复数的标准形式,根据所给的复数是一个纯虚数,得到实部等于0,虚部不等于0,解出结果.
【解答】解:∵z1=1﹣i,z2=a+2ai,
∴z1+z2=a+1+(2a﹣1)i,
∵复数z1+z2 是纯虚数,
∴a+1=0,2a﹣1≠0,
∴a=﹣1,
故答案为:﹣1.
【点评】本题考查复数的基本概念和加减运算,是一个基础题,解题的关键是看清题目中的要求,注意一定要上虚部不等于0.
3.经过圆(x﹣1)2+y2=1的圆心M,且与直线x﹣y=0垂直的直线方程是 x+y﹣1=0 .
【考点】圆的切线方程.
【专题】计算题;方程思想;综合法;圆锥曲线的定义、性质与方程.
【分析】易得圆心坐标,由垂直关系可得直线的斜率,可得点斜式方程,化为一般式即可.
【解答】解:圆(x﹣1)2+y2=1的圆心M为(1,0),
又直线x﹣y=0的斜率为1,
由垂直关系可得要求直线的斜率为﹣1,
∴直线方程为y﹣0=﹣(x﹣1),即x+y﹣1=0.
故答案为:x+y﹣1=0.
【点评】本题考查直线的一般式方程和垂直关系,涉及圆的标准方程,属基础题.
4.△ABC中,a,b,c分别是角A,B,C的对边,,则A= 45° .
【考点】正弦定理.
【专题】计算题.
【分析】由a,b及sinB的值,利用正弦定理求出sinA的值,再由a小于b,利用三角形中大边对大角得到A小于B,确定出A的范围,进而由sinA的值,利用特殊角的三角函数值即可求出A的度数.
【解答】解:∵a=,b=,B=60°,
∴由正弦定理=得:sinA==,
又<,即a<b,∴A<B,
则A=45°.
故答案为:45°
【点评】此题考查了正弦定理,三角形的边角关系,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.
5.已知数列{an}是等差数列,且a1+a7+a13=2π,则tan(a2+a12)═ .
【考点】等差数列的性质.
【专题】等差数列与等比数列.
【分析】由等差数列的性质易得a7=,进而可得tan(a2+a12)=tan(2a7),代值计算可得.
【解答】解:由等差数列的性质可得a1+a7+a13=3a7=2π,∴a7=,
∴tan(a2+a12)=tan(2a7)=tan=
故答案为:
【点评】本题考查等差数列的性质,涉及正切的运算,属基础题.
6.若命题“ x∈R,使得x2+(a﹣1)x+1<0”是真命题,则实数a的取值范围是 (﹣∞,﹣1)∪(3,+∞) .
【考点】二次函数的性质.
【专题】计算题.
【分析】因为不等式对应的是二次函数,其开口向上,若“ x∈R,使得x2+(a﹣1)x+1<0”,则相应二次方程有不等的实根.
【解答】解:∵“ x∈R,使得x2+(a﹣1)x+1<0
∴x2+(a﹣1)x+1=0有两个不等实根
∴△=(a﹣1)2﹣4>0
∴a<﹣1或a>3
故答案为:(﹣∞,﹣1)∪(3,+∞)
【点评】本题主要考查一元二次不等式,二次函数,二次方程间的相互转化及相互应用,这是在函数中考查频率较高的题目,灵活多变,难度可大可小,是研究函数的重要方面.
7.对任意非零实数a、b,定义一种运算:a b,其结果y=a b的值由如图确定,则= 1 .
【考点】程序框图.
【专题】计算题;图表型;分类讨论;算法和程序框图.
【分析】通过程序框图判断出新运算S=a b的解析式,化简,再利用新运算法则求出值.
【解答】解:由程序框图知 S=a b=,
∴=3 4==1
故答案为:1.
【点评】本题考查判断程序框图的功能即判断出新运算法则.利用运算法则求值,属于基础题.
8.(理科)极坐标系中两点,,则线段AB的长等于 .
【考点】由三视图求面积、体积.
【专题】数形结合;定义法;坐标系和参数方程.
【分析】根据极坐标系中两点间的距离公式,求出线段AB的长即可.
【解答】解:极坐标系中,,
∴线段AB的长为
|AB|==.
故答案为:.
【点评】本题考查了极坐标系中两点间的距离公式的应用问题,是基础题目.
9.一个几何体的三视图如图所示,则该几何体的体积等于 .
【考点】由三视图求面积、体积.
【专题】计算题.
【分析】由三视图知,原几何体是一个球和一个正方体构成的组合体,再根据三视图得到球的半径和正方体的棱长,即可求体积
【解答】解:由三视图知原几何体是一个球和一个正方体构成的组合体,球的直径为2,半径为1,正方体的棱长为2
∴原几何体的体积为:
故答案为:
【点评】本题考查三视图,要求能把三视图还原成原几何体,能根据三视图找到原几何体的长度关系,要求有较好的空间想象力.属简单题
10.若关于x,y的二元一次方程组至多有一组解,则实数m的取值范围是 (﹣∞,1)∪(1,+∞) .
【考点】系数矩阵的逆矩阵解方程组;二元一次方程组的矩阵形式.
【专题】计算题.
【分析】先根据矩阵的乘法进行化简得到二元一次方程组,然后消去y得(m2﹣1)x=m(m﹣1),当m﹣1≠0时(m2﹣1)x=m(m﹣1)至多有一组解,从而求出m的范围.
【解答】解:关于x,y的二元一次方程组
即二元一次方程组
①×m﹣②得(m2﹣1)x=m(m﹣1)
当m﹣1≠0时(m2﹣1)x=m(m﹣1)至多有一组解
∴m≠1
故答案为:(﹣∞,1)∪(1,+∞)
【点评】本题主要考查了二元一次方程组的解的个数,以及矩阵的乘法运算,属于中档题.
11.从集合A={﹣1,1,2}中随机选取一个数记为k,从集合B={﹣2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第三象限的概率为 .
【考点】古典概型及其概率计算公式.
【专题】计算题;概率与统计.
【分析】本题是一个古典概型,试验发生包含的事件(k,b)的取值所有可能的结果可以列举出,满足条件的事件直线不经过第三象限,符合条件的(k,b)有2种结果,根据古典概型概率公式得到结果.
【解答】解:由题意知本题是一个古典概型,试验发生包含的事件k∈A={﹣1,1,2},b∈B={﹣2,1,2},
得到(k,b)的取值所有可能的结果有:(﹣1,﹣2);(﹣1,1);(﹣1,2);(1,﹣2);(1,1);(1,2);
(2,﹣2);(2,1);(2,2)共9种结果.
而当时,直线不经过第三象限,符合条件的(k,b)有2种结果,
∴直线不过第四象限的概率P=,
故答案为.
【点评】古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、体积的比值得到,属于基础题.
12.不等式sin2x+acosx+a2≥1+cosx对一切x∈R成立,则实数a的取值范围为 a≥1或a≤﹣2 .
【考点】三角函数的最值;三角函数中的恒等变换应用.
【专题】函数的性质及应用;三角函数的图像与性质.
【分析】不等式进行等价转化为关于cosx的一元二次不等式,利用二次函数的性质和图象列不等式组求得答案.
【解答】解;不等式等价于1﹣cos2x+acosx+a2﹣1﹣cosx≥0,恒成立,
整理得﹣cos2x+(a﹣1)cosx+a2≥0,
设cosx=t,则﹣1≤t≤1,
g(t)=﹣t2+(a﹣1)t+a2,要使不等式恒成立需
,求得a≥1或a≤﹣2,
故答案为:a≥1或a≤﹣2.
【点评】本题主要考查了一元二次不等式的解法,二次函数的性质.注重了对数形结合思想的运用和问题的分析.
13.如图已知每条棱长都为3的直平行六面体ABCD﹣A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为 .
【考点】棱柱、棱锥、棱台的体积;棱柱的结构特征.
【专题】计算题.
【分析】先推导点P的轨迹,从而确定点P与平行六面体所围成的几何体的形状,然后求几何体的体积
【解答】解:取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
以DE所在直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立如图空间直角坐标系
设M(0,0,z),N(x,y,0),则P()
MN=
∴x2+y2+z2=4
∴
∴OP2=1
即OP=1
∴点P的轨迹是以原点D为球心,以1为半径的球的一部分
又∵∠BAD=60°
∴∠ADC=120°
∴点P的轨迹是球的
∴几何体的体积为
故答案为:
【点评】本题考查几何体的体积,须先用代数法确定点的轨迹,然后熟练应用体积公式即可.属中档题
14.在平面直角坐标系中,定义(n∈N*为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么的值为= 2+ .
【考点】数列的极限.
【专题】新定义;转化思想;分析法;等差数列与等比数列.
【分析】由题设知a1=|(0,1) (1,1)|=1,a2=|(1,1) (0,2)|=,a3=|(0,2) (2,2)|=2,a4=|(2,2) (0,4)|=2,…,an=()n﹣1,Sn=a1+a2+a3+…+an=.由此可求出的值.
【解答】解:由题设知P1(0,1),P2(1,1),a1=|P1P2|=1,
且当n≥2时,an2=|PnPn+1|2=(xn+1﹣xn)2﹣(yn+1﹣yn)2
=[(yn﹣xn)﹣xn]2+[(yn+xn)﹣yn]2=5xn2﹣4xnyn+yn2
an﹣12=|Pn﹣1Pn|2=(xn﹣xn﹣1)2﹣(yn﹣yn﹣1)2①
由定义(n∈N),得,
∴,
代入①计算化简得an﹣12=|Pn﹣1Pn|2=()2+()2=(5xn2﹣4xnyn+yn2)=an2.
∴=(n≥2),
∴数列{an}是以为公比的等比数列,且首项a1=1,
∴an=()n﹣1,
∴Sn=a1+a2+a3+…+an=.
∴= =,
则===2+.
故答案为:.
【点评】本题考查集合的性质和运算,解题时要注意等比数列前n项和公式的合理运用,属于中档题.
15.若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:
①τ={ ,{a},{c},{a,b,c}};
②τ={ ,{b},{c},{b,c},{a,b,c}};
③τ={ ,{a},{a,b},{a,c}};
④τ={ ,{a,c},{b,c},{c},{a,b,c}}.
其中是集合X上的拓扑的集合τ的序号是 ②④ .
【考点】集合的包含关系判断及应用.
【专题】压轴题;新定义.
【分析】根据集合X上的拓扑的集合τ的定义,逐个验证即可:①{a}∪{c}={a,c} τ,③{a,b}∪{a,c}={a,b,c} τ,因此①③都不是;
②④满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ,因此②④是,从而得到答案.
【解答】解:①τ={ ,{a},{c},{a,b,c}};
而{a}∪{c}={a,c} τ,故①不是集合X上的拓扑的集合τ;
②τ={ ,{b},{c},{b,c},{a,b,c}},满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ
因此②是集合X上的拓扑的集合τ;
③τ={ ,{a},{a,b},{a,c}};
而{a,b}∪{a,c}={a,b,c} τ,故③不是集合X上的拓扑的集合τ;
④τ={ ,{a,c},{b,c},{c},{a,b,c}}.
满足:①X属于τ, 属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ
因此④是集合X上的拓扑的集合τ;
故答案为②④.
【点评】此题是基础题.这是考查学生理解能力和对知识掌握的灵活程度的问题,重在理解题意.本题是开放型的问题,要认真分析条件,探求结论,对分析问题解决问题的能力要求较高.
二、选择题(本题满分16分)本大题共有5题,每题都给出四个结论,其中有且只有一个结论是正确的选对得4分,否则一律得零分.
16.A,B两点在半径为2的球面上,且以线段AB为直径的小圆周长为2π,则A,B两点间的球面距离为( )
A.π B.2π C. D.
【考点】多面体和旋转体表面上的最短距离问题.
【专题】数形结合;数形结合法;立体几何.
【分析】求出球的半径,利用等边三角形求出∠AOB的大小,再求球面距离弧AB.
【解答】解:根据题意画出示意图,如图所示:
∵球的半径为R=2,且以线段AB为直径的小圆周长为2π,
∴小圆直径为AB=2;
∴在三角形AOB中,AO=AB=BO=2,
∴∠AOB=,
∴A,B两点间的球面距离为:l=R=.
故选:D.
【点评】本题考查了球面距离的应用问题,也考查了圆的周长与弧长的计算问题,是基础题目.
17.已知函数,则“f(2)<f(3)”是“f(x)在区间(﹣2,+∞)上单调递增”的什么条件.( )
A.“充要” B.“充分不必要”
C.“必要不充分” D.“既不充分也不必要”
【考点】必要条件、充分条件与充要条件的判断.
【专题】函数思想;综合法;圆锥曲线的定义、性质与方程.
【分析】先求出函数f(x)的导数,求出“f(x)在区间(﹣2,+∞)上单调递增”的充要条件,从而得到答案.
【解答】解:f′(x)==,
如f(x)在区间(﹣2,+∞)上单调递增,
则2a﹣1>0,解得:a>,
由f(2)<f(3),得:<,解得:a>,
故f(2)<f(3)”是“f(x)在区间(﹣2,+∞)上单调递增”的充要条件,
故选:A.
【点评】本题考查了充分必要条件,考查函数的单调性问题,是一道基础题.
18.设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④M中所有直线均经过一个定点;
⑤不存在定点P不在M中的任一条直线上;
⑥对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上;
⑦M中的直线所能围成的正三角形面积都相等.
A.3 B.4 C.5 D.6
【考点】直线的斜截式方程.
【分析】根据已知可知直线系M都为以(0,2)为圆心,以1为半径的圆的切线,取半径为2即可得到所以①对;存在圆心为(0,2),半径为的圆与直线都不相交,所以②对;③显然对;④错;⑤错,存在可取一点(0,2)即可验证;⑥可去三角形的外接正三角形所有边均在M中的直线上且面积相等,所以⑥都正确.⑦可以举反例.
【解答】解:根据直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π)得到所有直线都为圆心为(0,2),半径为1的圆的切线;
可取圆心为(0,2),半径分别为2,,1得到①②③正确;所有的直线与一个圆相切,没有过定点,④错;存在(0,2)不在M中的任一条直线上,所以⑤错;存在等边三角形的三边都在M中的直线上,⑥对,可取圆的外接正三角形其所有边均在M中的直线上且面积相等;⑦可以做在圆的三等分点做圆的切线,把其中一条平移到另外两个点中点时,可知⑦错误;故①②③⑥正确,④⑤⑦错,所以真命题的个数为4个
故选:B
【点评】考查学生利用直线的斜截式方程得到直线系M为平面内除过一个圆的区域.
19.(2015秋 上海校级期中)在约束条件下,若3≤S≤5,则目标函数z=3x+2y的最大值变化范围是( )
A.[6,8] B.[6,15] C.[7,8] D.[7,15]
【考点】简单线性规划.
【专题】不等式的解法及应用.
【分析】先根据约束条件画出可行域,设z=3x+2y,再利用z的几何意义求最值,只需求出直线z=3x+2y过可行域内的点时,从而得到z=3x+2y的最大值即可.
【解答】解:先根据约束条件画出可行域,
设z=3x+2y,
将z的值转化为直线z=3x+2y在y轴上的截距,
当S=3时,对应的平面区域为四边形OCAD,
当直线z=3x+2y经过点A(1,2)时,z最大,最大值为7.
当S=5时,对应的平面区域为三角形OBD,
当直线z=3x+2y经过点B(0,4)时,z最大,最大值为8,
故当3≤S≤5时,目标函数z=3x+2y的最大值的变化范围是[7,8].
故选:C
【点评】本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,利用数形结合是解决本题的关键.
20.长度分别为2、x、x、x、x、x的六条线段能成为同一个四面体的六条棱的充要条件是( )
A.x B. C. D.x>1
【考点】棱锥的结构特征.
【专题】压轴题;探究型.
【分析】用极限的角度考虑,可求x接近最小的数值,得不到最大值,求出结果.
【解答】解:用极限的角度考虑,四面体趋近于在一个平面内的菱形时x最小,
不能低于,最大可以无穷大(就是两个等边三角形的二面角可以无限趋于0),
【点评】本题考查棱锥的结构特征,考查空间想象能力,极限思想的应用,是中档题.
三、解答题
21.关于x的不等式<0的解集为(﹣1,b).
(1)求实数a、b的值;
(2)若z1=a+bi,z2=cosα+isinα,且z1z2为纯虚数,求的值.
【考点】二阶矩阵;两角和与差的余弦函数.
【专题】计算题.
【分析】(1)将原不等式转化为(x+a)x﹣2<0,即x2+ax﹣2<0,根据解集为(﹣1,b)得到﹣1,b是方程x2+ax﹣2=0的两个根,结合根与系数的关系即可列出关于a,b的方程组,并利用解二元一次方程组的方法即可求解
(2)根据z1z2为纯虚数,得知实部为0,虚部不为0,即可得到关于α的条件式并解得:tanα=﹣,再利用两角差的余弦,倍角公式和同角的三角关系将化为关于tanα的代数式即可求解
【解答】解:(1)原不等式等价于(x+a)x﹣2<0,
即x2+ax﹣2<0
由题意得,
解得a=﹣1,b=2.
(2)z1=﹣1+2i,z1z2=(﹣cosα﹣2sinα)+i(2cosα﹣sinα)
若z1z2为纯虚数,则,
解得
==.
【点评】本题考查了二阶矩阵,两角和与差的余弦函数及解三角方程的能力,属于基础题.
22.如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为,求k的值
(3)现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
【考点】用空间向量求直线与平面的夹角;棱柱、棱锥、棱台的侧面积和表面积;直线与平面垂直的判定;直线与平面所成的角.
【专题】压轴题;空间位置关系与距离;空间角.
【分析】(1)取DC得中点E,连接BE,可证明四边形ABED是平行四边形,再利用勾股定理的逆定理可得BE⊥CD,即CD⊥AD,又侧棱AA1⊥底面ABCD,可得AA1⊥DC,利用线面垂直的判定定理即可证明.(2)通过建立空间直角坐标系,求出平面的法向量与斜线的方向向量的夹角即可得出;(3)由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案
新四棱柱共有此4种不同方案.写出每一方案下的表面积,通过比较即可得出f(k).
【解答】(1)证明:取DC的中点E,连接BE,∵AB∥ED,AB=ED=3k,
∴四边形ABED是平行四边形,
∴BE∥AD,且BE=AD=4k,∴BE2+EC2=(4k)2+(3k)2=(5k)2=BC2,∴∠BEC=90°,∴BE⊥CD,
又∵BE∥AD,∴CD⊥AD.
∵侧棱AA1⊥底面ABCD,∴AA1⊥CD,
∵AA1∩AD=A,∴CD⊥平面ADD1A1.
(2)解:以D为坐标原点,、、的方向为x,y,z轴的正方向建立空间直角坐标系,
则A(4k,0,0),C(0,6k,0),B1(4k,3k,1),A1(4k,0,1).
∴,,.
设平面AB1C的一个法向量为=(x,y,z),则,取y=2,则z=﹣6k,x=3.∴.
设AA1与平面AB1C所成角为θ,则===,解得k=1,故所求k=1.
(3)由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案新四棱柱共有此4种不同方案.
写出每一方案下的表面积,通过比较即可得出f(k)=
【点评】本题主要考查了线线、线面的位置关系、通过建立空间直角坐标系利用法向量求线面角、柱体的定义积表面积、勾股定理的逆定理等基础知识,考查了空间想象能力、推理能力和计算能力及化归与转化能力.
23.如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(﹣,C,内切圆圆心I(1,t).设A点的轨迹为L
(1)求L的方程;
(2)过点C作直线m交曲线L于不同的两点M、N,问在x轴上是否存在一个异于点C的定点Q.使对任意的直线m都成立?若存在,求出Q的坐标,若不存在,说明理由.
【考点】轨迹方程;直线与圆锥曲线的关系.
【专题】计算题.
【分析】(1)由切线长定理得,从一点出发的切线长相等,得到A点到两个点B,C的距离之差是常数,根据双曲线的定义得A点的轨迹是双曲线,从而即可求出L的方程;
(2)对于存在性问题,可先假设存在,设点Q(x0,0),再设M(x1,y1),N(x2,y2),由条件得∠MQC=∠NQC,下面分类讨论:①当MN⊥x,②当MN不垂直x时,第一种情况比较简单,对于第二种情况,将直线的方程代入双曲线方程,消去y得到关于x的二次方程,结合根与系数的关系,利用斜率相等求得,从而说明存在点Q.
【解答】解:(1)由题意|AD|=|AF|.|BD|=|BE|,|CE|=|CF|.
∴|AB|﹣|AC|=|BD|﹣|CF|=|BE|﹣|CE|=|BO|+|OE|﹣(|OC|﹣|OE|)=2|OE|
I(1,t),E(1,0),|OE|=1,|AB|﹣|AC|=2
x2﹣y2=1(x>1)
(2)设点Q(x0,0),设M(x1,y1),N(x2,y2)
∵ ∠MQC=∠NQC
于是:①当MN⊥x,点Q(x0,0)在x上任何一点处,都能够使得:
∠MQC=∠NQC成立,
②当MN不垂直x时,设直线.
由得:
则:
∴
∵,要使∠MQC=∠NQC成立,
只要tan∠MQC=tan∠NQC: x2y1﹣x0y1+x1y2﹣x0y2=0
即=
∴ ∴当时,能够使:
对任意的直线m成立.
【点评】本题主要考查了轨迹方程、直线与圆锥曲线的交点等知识,属于中档题.
24.设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件,试求Sn的最大值.
【考点】等差数列与等比数列的综合;数列的求和.
【专题】综合题;等差数列与等比数列.
【分析】(1)设{an}的公差为d,利用裂项法原等式可化为(﹣+﹣+…+﹣)=,整理可得(k﹣1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
(2)当k=1,b=0时,假设p是q的必要条件,分当n=1时,当n≥2时,当n≥3时讨论即可判断结论是否正确;
(3)由+≤M,可设a1=rcosθ,an+1=rsinθ,代入求和公式Sn=,利用三角函数的有界性即可求得其最大值.
【解答】解:(1)设{an}的公差为d,则原等式可化为(﹣+﹣+…+﹣)=,
所以 =,
即(k﹣1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…
(2)当k=1,b=0时,假设p是q的必要条件,即“若++…+=①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
当n=1时, =显然成立.…
当n≥2时,若++…+=②,
由①﹣②得, =(﹣),即nan﹣(n﹣1)an+1=a1③.
当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n﹣1)an﹣1﹣(n﹣2)an=a1④,即2an=an﹣1+an+1.所以{an}为等差数列,即p是q的必要条件.…
(3)由+≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤.
设{an}的公差为d,则an+1﹣a1=nd=rsinθ﹣rcosθ,
所以d=,
所以an=rsinθ﹣,
Sn==r≤ =,
所以Sn的最大值为…
【点评】本题考查等差数列与等比数列的综合,突出考查“充分、必要条件”在数列中的综合应用,判断(2)中“p是否为q的必要条件”是难点,考查参数方程及三角函数的有界性,属于难题.
25.已知f(x)=.
(1)求f(f(x));
(2)对参数a的哪些值,方程|x|+||=a正好有3个实数解;
(3)设b为任意实数,证明:x+﹣=b共有3个不同的实数解x1,x2,x3,并且x1+x2+x3=b.
【考点】根的存在性及根的个数判断;函数的值.
【专题】计算题;作图题;证明题;数形结合;函数的性质及应用.
【分析】(1)化简可得f(f(x))=f()=x,
(2)作函数y=||与函数y=a﹣|x|的图象,从而化为x+=a有一个解,从而利用判别式解得.
(3)化简方程可得x3﹣bx2+(b﹣21)x+2b﹣7=0,从而令g(x)=x3﹣bx2+(b﹣21)x+2b﹣7,从而利用零点的判定定理判断即可.
【解答】解:(1)∵f(x)=,
∴f(f(x))=f()=x,
(2)作函数y=||与函数y=a﹣|x|的图象如下,
若使方程|x|+||=a正好有3个实数解,
则x+=a有一个解,
即3x2﹣3ax+a+1=0有一个解,
故△=9a2﹣12a﹣12=0,
解得,a=2或a=﹣(舍去);
故a=2;
(3)证明:∵x+﹣=b,
∴=b,
∴x3﹣bx2+(b﹣21)x+2b﹣7=0,
令g(x)=x3﹣bx2+(b﹣21)x+2b﹣7,
易知g(x)=﹣∞,g(x)=+∞,
g(﹣1)=﹣1﹣b﹣b+21+2b﹣7=13>0,
g(2)=8﹣4b+2b﹣42+2b﹣7=﹣41<0,
故g(x)在(﹣∞,﹣1),(﹣1,2),(2,+∞)上各有一个零点,
故g(x)有3个不同的零点x1,x2,x3,
故x+﹣=b共有3个不同的实数解x1,x2,x3,
∵x3﹣bx2+(b﹣21)x+2b﹣7=(x﹣x1)(x﹣x2)(x﹣x3)
=x3﹣(x1+x2+x3)x2+(x1x2+x1x3+x3x2)x﹣x1x2x3,
故x1+x2+x3=b.
【点评】本题考查了数形结合的思想应用及分段函数的应用,同时考查了函数的零点与方程的根的关系应用.
同课章节目录
