江苏省盐城市东台市创新学校2015-2016学年高一(上)12月月考数学试卷(解析版)
文档属性
| 名称 | 江苏省盐城市东台市创新学校2015-2016学年高一(上)12月月考数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-25 00:00:00 | ||
图片预览




文档简介
2015-2016学年江苏省盐城市东台市创新学校高一(上)12月月考数学试卷
一.填空题(共14小题)
1.将弧度转化成角度: = .
2.设θ是第三象限角,则点P(sinθ,cosθ)在第 象限.
3.=(cosα,sinα),||= .
4.已知△ABC中,tanA=﹣,则cosA= .
5.函数y=sin(πx﹣)的最小正周期为 .
6.函数y=cos(﹣x)的单调递增区间为 .
7.平面向量=(2,1),=(m,﹣2),若与共线,则m的值为 .
8.函数y=的单调递增区间是 .
9.已知= .
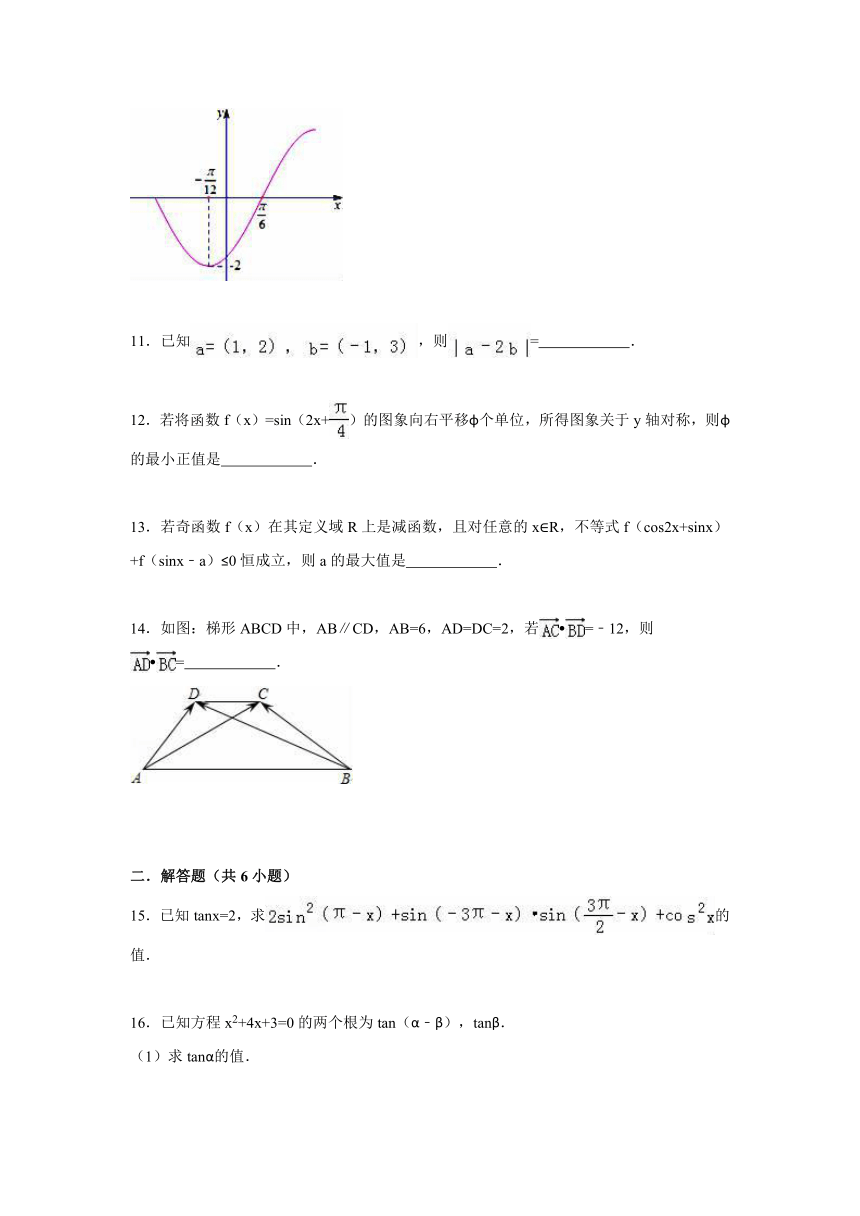
10.函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<的部分图象如图所示,则f(π)的值为 .
11.已知,则= .
12.若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是 .
13.若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是 .
14.如图:梯形ABCD中,AB∥CD,AB=6,AD=DC=2,若 =﹣12,则 = .
二.解答题(共6小题)
15.已知tanx=2,求的值.
16.已知方程x2+4x+3=0的两个根为tan(α﹣β),tanβ.
(1)求tanα的值.
(2)求的值.
17.已知A(3,1),B(t,﹣2),C(1,2t).
(1)若,求t;
(2)若∠BAC=90°,求t.
18.已知函数f(x)=2cos2ωx+2sinωxcosωx﹣1(ω>0)的最小正周期为π.
(1)求f()的值;
(2)求函数f(x)的单调递增区间及其图象的对称轴方程.
19.已知向量,的夹角为60°,且||=2,||=1,若=﹣4, =+2,求
(1) ;
(2)|+|.
20.解方程cos2x=cosx+sinx,求x的值.
2015-2016学年江苏省盐城市东台市创新学校高一(上)12月月考数学试卷
参考答案与试题解析
一.填空题(共14小题)
1.将弧度转化成角度: = 120° .
【考点】弧度与角度的互化.
【专题】三角函数的求值.
【分析】直接利用角度与弧度的转化化简即可.
【解答】解:因为π=180°,所以: ==120°
故答案为:120°.
【点评】本题考查角度与弧度的转化,基本知识的考查.
2.设θ是第三象限角,则点P(sinθ,cosθ)在第 三 象限.
【考点】三角函数值的符号.
【专题】三角函数的求值.
【分析】由题意可得sinθ<0,cosθ<0,可判点P在第三象限.
【解答】解:∵θ是第三象限角,∴sinθ<0,cosθ<0,
∴点P(sinθ,cosθ)在第三象限
故答案为:三
【点评】本题考查三角函数值的符号,属基础题.
3.=(cosα,sinα),||= 1 .
【考点】向量的模.
【专题】平面向量及应用.
【分析】利用向量模的计算公式即可得出.
【解答】解:∵ =(cosα,sinα),
∴==1.
故答案为:1.
【点评】本题考查了向量模的计算公式,属于基础题.
4.已知△ABC中,tanA=﹣,则cosA= ﹣ .
【考点】同角三角函数间的基本关系.
【专题】计算题.
【分析】△ABC中,由tanA=﹣<0,判断A为钝角,利用=﹣和sin2A+cos2A=1,求出cosA的值.
【解答】解:∵△ABC中,tanA=﹣,∴A为钝角,cosA<0.
由=﹣,sin2A+cos2A=1,可得cosA=﹣,
故答案为﹣.
【点评】本题考查同角三角函数的基本关系的应用,注意判断A为钝角.
5.函数y=sin(πx﹣)的最小正周期为 2 .
【考点】三角函数的周期性及其求法.
【专题】三角函数的图像与性质.
【分析】由三角函数的周期性及其求法直接求值.
【解答】解:∵y=sin(πx﹣),
∴由三角函数的周期性及其求法可得最小正周期T==2.
故答案为:2.
【点评】本题主要考查了三角函数的周期性及其求法,属于基本知识的考查.
6.函数y=cos(﹣x)的单调递增区间为 [2kπ﹣,2kπ+](k∈Z) .
【考点】余弦函数的单调性.
【专题】计算题;三角函数的图像与性质.
【分析】利用余弦的诱导公式可将y=cos(﹣x)转化为y=cos(x﹣),再利用余弦函数的单调性即可求得函数y=cos(﹣x)的单调递增区间.
【解答】解:∵y=cos(﹣x)=cos(x﹣),
由2kπ﹣π≤x﹣≤2kπ,k∈Z得:
2kπ﹣≤x≤2kπ+,k∈Z.
∴原函数的单调递增区间为[2kπ﹣,2kπ+](k∈Z).
故答案为:[2kπ﹣,2kπ+](k∈Z).
【点评】本题考查复合三角函数的单调性,着重考查余弦函数的诱导公式与单调性,属于基本知识的考查.
7.平面向量=(2,1),=(m,﹣2),若与共线,则m的值为 ﹣4 .
【考点】平面向量的坐标运算;平行向量与共线向量.
【专题】计算题.
【分析】运用平面向量共线的坐标表示列式后求m的值.
【解答】解:因为,,由与共线,所以2×(﹣2)﹣m=0,解得:m=﹣4.
故答案为﹣4.
【点评】本题考查了平面向量的坐标运算,考查了共线向量,若,则 x1y2﹣x2y1=0.
8.函数y=的单调递增区间是 [0,] .
【考点】两角和与差的余弦函数;正弦函数的图象.
【专题】三角函数的图像与性质.
【分析】化简可得y=sin(x+),解不等式2kπ﹣≤x+≤2kπ+可得函数所有的单调递增区间,结合x∈[0,]可得.
【解答】解:化简可得y=sinxcos+cosxsin=sin(x+),
由2kπ﹣≤x+≤2kπ+可得2kπ﹣≤x≤2kπ+,k∈Z,
当k=0时,可得函数的一个单调递增区间为[﹣,],
由x∈[0,]可得x∈[0,],
故答案为:[0,].
【点评】本题考查两角和与差的三角函数,涉及三角函数的单调性,属基础题.
9.已知= .
【考点】同角三角函数基本关系的运用.
【分析】将1=sin2α+cos2α代入,分子分母同时除以cos2α可得到关于tanα的关系式,即可得到答案.
【解答】解:∵ ==
又∵tanα=﹣∴原式=
故答案为:.
【点评】本题主要考查同角三角三角函数的基本关系.注意形式的转化.
10.函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<的部分图象如图所示,则f(π)的值为 ﹣ .
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.
【专题】三角函数的图像与性质.
【分析】由周期求出ω,由特殊点的坐标结合φ的范围出φ的值,可得函数的解析式.
【解答】解析:由图可知,∴ω=2,
∴f(x)=2sin(2x+φ).
∵,∴.再根据,
∴,∴,∴,
故答案为:﹣.
【点评】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,属于基础题.
11.已知,则= 5 .
【考点】平面向量的坐标运算.
【专题】平面向量及应用.
【分析】直接利用向量模的求法,求解即可.
【解答】解:,则=|(3,﹣4)|==5.
故答案为:.
【点评】.本题考查向量的模的求法,向量的坐标运算,基本知识的考查.
12.若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是 .
【考点】函数y=Asin(ωx+φ)的图象变换.
【专题】三角函数的图像与性质.
【分析】根据函数y=Asin(ωx+φ)的图象变换规律,可得所得图象对应的函数解析式为y=sin(2x+﹣2φ),再根据所得图象关于y轴对称可得﹣2φ=kπ+,k∈z,由此求得φ的最小正值.
【解答】解:将函数f(x)=sin(2x+)的图象向右平移φ个单位,
所得图象对应的函数解析式为y=sin[2(x﹣φ)+]=sin(2x+﹣2φ)关于y轴对称,
则﹣2φ=kπ+,k∈z,即 φ=﹣﹣,故φ的最小正值为,
故答案为:.
【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性,属于中档题.
13.若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是 ﹣3 .
【考点】二倍角的余弦;奇偶性与单调性的综合;复合三角函数的单调性.
【专题】计算题;证明题;压轴题.
【分析】根据函数是奇函数且在R上是减函数,将原不等式变形为cos2x+2sinx≥a恒成立,结合二倍角的三角函数公式和二次函数在闭区间上求最值的方法,即可得到a的最大值.
【解答】解:不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,即f(cos2x+sinx)≤﹣f(sinx﹣a)恒成立
又∵f(x)是奇函数,﹣f(sinx﹣a)=f(﹣sinx+a)
∴不等式f(cos2x+sinx)≤f(﹣sinx+a)在R上恒成立
∵函数f(x)在其定义域R上是减函数,
∴cos2x+sinx≥﹣sinx+a,即cos2x+2sinx≥a
∵cos2x=1﹣2sin2x,∴cos2x+2sinx=﹣2sin2x+2sinx+1,
当sinx=﹣1时cos2x+2sinx有最小值﹣3.
因此a≤﹣3,a的最大值是﹣3
故答案为:﹣3
【点评】本题在已知函数f(x)的单调性的奇偶性的前提下,解决一个不等式恒成立的问题,着重考查了函数的单调性和奇偶性、二倍角的三角函数公式和二次函数在闭区间上求最值等知识,属于基础题.
14.如图:梯形ABCD中,AB∥CD,AB=6,AD=DC=2,若 =﹣12,则 = 0 .
【考点】平面向量数量积的运算.
【专题】平面向量及应用.
【分析】首先,设,为基底,然后,根据 =﹣12,得到∠BAD=60°然后根据数量积的运算求解即可.
【解答】解:以,为基底,则=+, =﹣,
则=﹣
=4﹣8cos∠BAD﹣12
=﹣12,
∴cos∠BAD=,则∠BAD=60°,
则=
=
=
=4﹣4=0.
故答案为:0.
【点评】本题主要考查平面向量的数量积,体现化归转化思想.另本题还可通过建立平面直角坐标系将向量“坐标化”来解决.向量问题突出基底法和坐标法,但要关注基底的选择与坐标系位置选择的合理性,两种方法之间的选择.
二.解答题(共6小题)
15.已知tanx=2,求的值.
【考点】同角三角函数基本关系的运用.
【专题】三角函数的求值.
【分析】原式利用诱导公式化简,再利用同角三角函数间的基本关系变形,将tanx的值代入计算即可求出值.
【解答】解:∵tanx=2,
∴原式=2sin2x﹣sinxcosx+cos2x
=
=
=.
【点评】此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.
16.已知方程x2+4x+3=0的两个根为tan(α﹣β),tanβ.
(1)求tanα的值.
(2)求的值.
【考点】两角和与差的正切函数;同角三角函数基本关系的运用.
【专题】计算题;三角函数的求值.
【分析】(1)α=(α﹣β)+β,利用两角和的正切公式即可求得tanα的值;
(2)将中的弦化切即可.
【解答】解:(1)∵α=(α﹣β)+β,
∴,
∴tanα=tan[(α﹣β)+β]= = =2.
(2)===﹣5.
【点评】本题考查两角和与差的正切函数,考查“弦”化“切”,考查转化思想与运算能力,属于中档题.
17.已知A(3,1),B(t,﹣2),C(1,2t).
(1)若,求t;
(2)若∠BAC=90°,求t.
【考点】平面向量数量积的坐标表示、模、夹角.
【分析】(1)由已知中A(3,1),B(t,﹣2),我们要以求出向量的坐标(含参数t),根据,构造关于t的方程,解方程即可得到答案.
(2)由∠BAC=90°,可得⊥,即 =0,将向量、的坐标代入向量数量积坐标运算公式,构造关于t的方程,解方程即可得到答案.
【解答】解:(1)∵A(3,1),B(t,﹣2),
∴=(t﹣3,﹣3),
又∵,
即=5,
解得t=7或t=﹣1.
(2)若∠BAC=90°,由题意知⊥,
又∵=(﹣2,2t﹣1),
∴(t﹣3) (﹣2)﹣3(2t﹣1)=﹣8t+9=0
解得t=.
【点评】本题考查的知识点是平面向量数量积的坐标表示及向量的模,其中根据向量的坐标运算公式,构造关于t的方程是解答本题的关键.
18.已知函数f(x)=2cos2ωx+2sinωxcosωx﹣1(ω>0)的最小正周期为π.
(1)求f()的值;
(2)求函数f(x)的单调递增区间及其图象的对称轴方程.
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;三角函数的化简求值;三角函数中的恒等变换应用;复合三角函数的单调性.
【分析】(1)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2ωx+),由此求得f()的值.
(2)由2kπ﹣≤2x+≤2kπ+,k∈z,求出函数f(x)的单调递增区间.由 2x+=kπ+求得 x的值,从而得到f(x)图象的对称轴方程.
【解答】解:(1)函数f(x)=2cos2ωx+2sinωxcosωx﹣1=cos2ωx+sin2ωx=2sin(2ωx+),
因为f(x)最小正周期为π,所以=π,解得ω=1,
所以f(x)=2sin(2x+),f()=2sin=1.
(2)由2kπ﹣≤2x+≤2kπ+,k∈z,可得 kπ﹣≤x≤kπ+,k∈z,
所以,函数f(x)的单调递增区间为[kπ﹣,kπ+],k∈z.
由 2x+=kπ+可得 x=kπ+,k∈z.
所以,f(x)图象的对称轴方程为x=kπ+,k∈z.…
【点评】本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性,属于中档题.
19.已知向量,的夹角为60°,且||=2,||=1,若=﹣4, =+2,求
(1) ;
(2)|+|.
【考点】平面向量数量积的性质及其运算律.
【专题】平面向量及应用.
【分析】(1)利用数量积的定义即可得出;
(2)利用向量模的计算公式即可得出.
【解答】解:(1)==2×1×=1;
(2)∵=,∴ ===2=2=2.
【点评】熟练掌握向量的数量积的定义和模的计算公式是解题的关键.
20.解方程cos2x=cosx+sinx,求x的值.
【考点】二倍角的余弦;任意角的三角函数的定义.
【专题】计算题;压轴题.
【分析】本题是一个三角恒等变换问题,解题的关键是减小角的倍数,化异为同,利用方程的思想解题是三角函数常见的做法,最后是给值求角的问题,注意不要漏解.
【解答】解:∵cos2x=cosx+sinx,
∴cos2x﹣sin2x=cosx+sinx,
∴(cosx+sinx)(cosx﹣sinx)﹣(cosx+sinx)=0,
∴(cosx+sinx)(cosx﹣sinx﹣1)=0.
如果cosx+sinx=0,则得1+tgx=0,tgx=﹣1,
解
如果cosx+sinx﹣1=0则得cosx﹣sinx=1,
∴,∴,
∴,∴.
综上,x=.
【点评】本题是一个三角恒等变换问题,与初中学习锐角三角函数一样,高中也要研究同角三角函数之间关系,弄清同角各不同三角函数之间的联系,实现不同函数值之间的互相转化.
一.填空题(共14小题)
1.将弧度转化成角度: = .
2.设θ是第三象限角,则点P(sinθ,cosθ)在第 象限.
3.=(cosα,sinα),||= .
4.已知△ABC中,tanA=﹣,则cosA= .
5.函数y=sin(πx﹣)的最小正周期为 .
6.函数y=cos(﹣x)的单调递增区间为 .
7.平面向量=(2,1),=(m,﹣2),若与共线,则m的值为 .
8.函数y=的单调递增区间是 .
9.已知= .
10.函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<的部分图象如图所示,则f(π)的值为 .
11.已知,则= .
12.若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是 .
13.若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是 .
14.如图:梯形ABCD中,AB∥CD,AB=6,AD=DC=2,若 =﹣12,则 = .
二.解答题(共6小题)
15.已知tanx=2,求的值.
16.已知方程x2+4x+3=0的两个根为tan(α﹣β),tanβ.
(1)求tanα的值.
(2)求的值.
17.已知A(3,1),B(t,﹣2),C(1,2t).
(1)若,求t;
(2)若∠BAC=90°,求t.
18.已知函数f(x)=2cos2ωx+2sinωxcosωx﹣1(ω>0)的最小正周期为π.
(1)求f()的值;
(2)求函数f(x)的单调递增区间及其图象的对称轴方程.
19.已知向量,的夹角为60°,且||=2,||=1,若=﹣4, =+2,求
(1) ;
(2)|+|.
20.解方程cos2x=cosx+sinx,求x的值.
2015-2016学年江苏省盐城市东台市创新学校高一(上)12月月考数学试卷
参考答案与试题解析
一.填空题(共14小题)
1.将弧度转化成角度: = 120° .
【考点】弧度与角度的互化.
【专题】三角函数的求值.
【分析】直接利用角度与弧度的转化化简即可.
【解答】解:因为π=180°,所以: ==120°
故答案为:120°.
【点评】本题考查角度与弧度的转化,基本知识的考查.
2.设θ是第三象限角,则点P(sinθ,cosθ)在第 三 象限.
【考点】三角函数值的符号.
【专题】三角函数的求值.
【分析】由题意可得sinθ<0,cosθ<0,可判点P在第三象限.
【解答】解:∵θ是第三象限角,∴sinθ<0,cosθ<0,
∴点P(sinθ,cosθ)在第三象限
故答案为:三
【点评】本题考查三角函数值的符号,属基础题.
3.=(cosα,sinα),||= 1 .
【考点】向量的模.
【专题】平面向量及应用.
【分析】利用向量模的计算公式即可得出.
【解答】解:∵ =(cosα,sinα),
∴==1.
故答案为:1.
【点评】本题考查了向量模的计算公式,属于基础题.
4.已知△ABC中,tanA=﹣,则cosA= ﹣ .
【考点】同角三角函数间的基本关系.
【专题】计算题.
【分析】△ABC中,由tanA=﹣<0,判断A为钝角,利用=﹣和sin2A+cos2A=1,求出cosA的值.
【解答】解:∵△ABC中,tanA=﹣,∴A为钝角,cosA<0.
由=﹣,sin2A+cos2A=1,可得cosA=﹣,
故答案为﹣.
【点评】本题考查同角三角函数的基本关系的应用,注意判断A为钝角.
5.函数y=sin(πx﹣)的最小正周期为 2 .
【考点】三角函数的周期性及其求法.
【专题】三角函数的图像与性质.
【分析】由三角函数的周期性及其求法直接求值.
【解答】解:∵y=sin(πx﹣),
∴由三角函数的周期性及其求法可得最小正周期T==2.
故答案为:2.
【点评】本题主要考查了三角函数的周期性及其求法,属于基本知识的考查.
6.函数y=cos(﹣x)的单调递增区间为 [2kπ﹣,2kπ+](k∈Z) .
【考点】余弦函数的单调性.
【专题】计算题;三角函数的图像与性质.
【分析】利用余弦的诱导公式可将y=cos(﹣x)转化为y=cos(x﹣),再利用余弦函数的单调性即可求得函数y=cos(﹣x)的单调递增区间.
【解答】解:∵y=cos(﹣x)=cos(x﹣),
由2kπ﹣π≤x﹣≤2kπ,k∈Z得:
2kπ﹣≤x≤2kπ+,k∈Z.
∴原函数的单调递增区间为[2kπ﹣,2kπ+](k∈Z).
故答案为:[2kπ﹣,2kπ+](k∈Z).
【点评】本题考查复合三角函数的单调性,着重考查余弦函数的诱导公式与单调性,属于基本知识的考查.
7.平面向量=(2,1),=(m,﹣2),若与共线,则m的值为 ﹣4 .
【考点】平面向量的坐标运算;平行向量与共线向量.
【专题】计算题.
【分析】运用平面向量共线的坐标表示列式后求m的值.
【解答】解:因为,,由与共线,所以2×(﹣2)﹣m=0,解得:m=﹣4.
故答案为﹣4.
【点评】本题考查了平面向量的坐标运算,考查了共线向量,若,则 x1y2﹣x2y1=0.
8.函数y=的单调递增区间是 [0,] .
【考点】两角和与差的余弦函数;正弦函数的图象.
【专题】三角函数的图像与性质.
【分析】化简可得y=sin(x+),解不等式2kπ﹣≤x+≤2kπ+可得函数所有的单调递增区间,结合x∈[0,]可得.
【解答】解:化简可得y=sinxcos+cosxsin=sin(x+),
由2kπ﹣≤x+≤2kπ+可得2kπ﹣≤x≤2kπ+,k∈Z,
当k=0时,可得函数的一个单调递增区间为[﹣,],
由x∈[0,]可得x∈[0,],
故答案为:[0,].
【点评】本题考查两角和与差的三角函数,涉及三角函数的单调性,属基础题.
9.已知= .
【考点】同角三角函数基本关系的运用.
【分析】将1=sin2α+cos2α代入,分子分母同时除以cos2α可得到关于tanα的关系式,即可得到答案.
【解答】解:∵ ==
又∵tanα=﹣∴原式=
故答案为:.
【点评】本题主要考查同角三角三角函数的基本关系.注意形式的转化.
10.函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<的部分图象如图所示,则f(π)的值为 ﹣ .
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.
【专题】三角函数的图像与性质.
【分析】由周期求出ω,由特殊点的坐标结合φ的范围出φ的值,可得函数的解析式.
【解答】解析:由图可知,∴ω=2,
∴f(x)=2sin(2x+φ).
∵,∴.再根据,
∴,∴,∴,
故答案为:﹣.
【点评】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,属于基础题.
11.已知,则= 5 .
【考点】平面向量的坐标运算.
【专题】平面向量及应用.
【分析】直接利用向量模的求法,求解即可.
【解答】解:,则=|(3,﹣4)|==5.
故答案为:.
【点评】.本题考查向量的模的求法,向量的坐标运算,基本知识的考查.
12.若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是 .
【考点】函数y=Asin(ωx+φ)的图象变换.
【专题】三角函数的图像与性质.
【分析】根据函数y=Asin(ωx+φ)的图象变换规律,可得所得图象对应的函数解析式为y=sin(2x+﹣2φ),再根据所得图象关于y轴对称可得﹣2φ=kπ+,k∈z,由此求得φ的最小正值.
【解答】解:将函数f(x)=sin(2x+)的图象向右平移φ个单位,
所得图象对应的函数解析式为y=sin[2(x﹣φ)+]=sin(2x+﹣2φ)关于y轴对称,
则﹣2φ=kπ+,k∈z,即 φ=﹣﹣,故φ的最小正值为,
故答案为:.
【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性,属于中档题.
13.若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是 ﹣3 .
【考点】二倍角的余弦;奇偶性与单调性的综合;复合三角函数的单调性.
【专题】计算题;证明题;压轴题.
【分析】根据函数是奇函数且在R上是减函数,将原不等式变形为cos2x+2sinx≥a恒成立,结合二倍角的三角函数公式和二次函数在闭区间上求最值的方法,即可得到a的最大值.
【解答】解:不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,即f(cos2x+sinx)≤﹣f(sinx﹣a)恒成立
又∵f(x)是奇函数,﹣f(sinx﹣a)=f(﹣sinx+a)
∴不等式f(cos2x+sinx)≤f(﹣sinx+a)在R上恒成立
∵函数f(x)在其定义域R上是减函数,
∴cos2x+sinx≥﹣sinx+a,即cos2x+2sinx≥a
∵cos2x=1﹣2sin2x,∴cos2x+2sinx=﹣2sin2x+2sinx+1,
当sinx=﹣1时cos2x+2sinx有最小值﹣3.
因此a≤﹣3,a的最大值是﹣3
故答案为:﹣3
【点评】本题在已知函数f(x)的单调性的奇偶性的前提下,解决一个不等式恒成立的问题,着重考查了函数的单调性和奇偶性、二倍角的三角函数公式和二次函数在闭区间上求最值等知识,属于基础题.
14.如图:梯形ABCD中,AB∥CD,AB=6,AD=DC=2,若 =﹣12,则 = 0 .
【考点】平面向量数量积的运算.
【专题】平面向量及应用.
【分析】首先,设,为基底,然后,根据 =﹣12,得到∠BAD=60°然后根据数量积的运算求解即可.
【解答】解:以,为基底,则=+, =﹣,
则=﹣
=4﹣8cos∠BAD﹣12
=﹣12,
∴cos∠BAD=,则∠BAD=60°,
则=
=
=
=4﹣4=0.
故答案为:0.
【点评】本题主要考查平面向量的数量积,体现化归转化思想.另本题还可通过建立平面直角坐标系将向量“坐标化”来解决.向量问题突出基底法和坐标法,但要关注基底的选择与坐标系位置选择的合理性,两种方法之间的选择.
二.解答题(共6小题)
15.已知tanx=2,求的值.
【考点】同角三角函数基本关系的运用.
【专题】三角函数的求值.
【分析】原式利用诱导公式化简,再利用同角三角函数间的基本关系变形,将tanx的值代入计算即可求出值.
【解答】解:∵tanx=2,
∴原式=2sin2x﹣sinxcosx+cos2x
=
=
=.
【点评】此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.
16.已知方程x2+4x+3=0的两个根为tan(α﹣β),tanβ.
(1)求tanα的值.
(2)求的值.
【考点】两角和与差的正切函数;同角三角函数基本关系的运用.
【专题】计算题;三角函数的求值.
【分析】(1)α=(α﹣β)+β,利用两角和的正切公式即可求得tanα的值;
(2)将中的弦化切即可.
【解答】解:(1)∵α=(α﹣β)+β,
∴,
∴tanα=tan[(α﹣β)+β]= = =2.
(2)===﹣5.
【点评】本题考查两角和与差的正切函数,考查“弦”化“切”,考查转化思想与运算能力,属于中档题.
17.已知A(3,1),B(t,﹣2),C(1,2t).
(1)若,求t;
(2)若∠BAC=90°,求t.
【考点】平面向量数量积的坐标表示、模、夹角.
【分析】(1)由已知中A(3,1),B(t,﹣2),我们要以求出向量的坐标(含参数t),根据,构造关于t的方程,解方程即可得到答案.
(2)由∠BAC=90°,可得⊥,即 =0,将向量、的坐标代入向量数量积坐标运算公式,构造关于t的方程,解方程即可得到答案.
【解答】解:(1)∵A(3,1),B(t,﹣2),
∴=(t﹣3,﹣3),
又∵,
即=5,
解得t=7或t=﹣1.
(2)若∠BAC=90°,由题意知⊥,
又∵=(﹣2,2t﹣1),
∴(t﹣3) (﹣2)﹣3(2t﹣1)=﹣8t+9=0
解得t=.
【点评】本题考查的知识点是平面向量数量积的坐标表示及向量的模,其中根据向量的坐标运算公式,构造关于t的方程是解答本题的关键.
18.已知函数f(x)=2cos2ωx+2sinωxcosωx﹣1(ω>0)的最小正周期为π.
(1)求f()的值;
(2)求函数f(x)的单调递增区间及其图象的对称轴方程.
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;三角函数的化简求值;三角函数中的恒等变换应用;复合三角函数的单调性.
【分析】(1)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2ωx+),由此求得f()的值.
(2)由2kπ﹣≤2x+≤2kπ+,k∈z,求出函数f(x)的单调递增区间.由 2x+=kπ+求得 x的值,从而得到f(x)图象的对称轴方程.
【解答】解:(1)函数f(x)=2cos2ωx+2sinωxcosωx﹣1=cos2ωx+sin2ωx=2sin(2ωx+),
因为f(x)最小正周期为π,所以=π,解得ω=1,
所以f(x)=2sin(2x+),f()=2sin=1.
(2)由2kπ﹣≤2x+≤2kπ+,k∈z,可得 kπ﹣≤x≤kπ+,k∈z,
所以,函数f(x)的单调递增区间为[kπ﹣,kπ+],k∈z.
由 2x+=kπ+可得 x=kπ+,k∈z.
所以,f(x)图象的对称轴方程为x=kπ+,k∈z.…
【点评】本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性,属于中档题.
19.已知向量,的夹角为60°,且||=2,||=1,若=﹣4, =+2,求
(1) ;
(2)|+|.
【考点】平面向量数量积的性质及其运算律.
【专题】平面向量及应用.
【分析】(1)利用数量积的定义即可得出;
(2)利用向量模的计算公式即可得出.
【解答】解:(1)==2×1×=1;
(2)∵=,∴ ===2=2=2.
【点评】熟练掌握向量的数量积的定义和模的计算公式是解题的关键.
20.解方程cos2x=cosx+sinx,求x的值.
【考点】二倍角的余弦;任意角的三角函数的定义.
【专题】计算题;压轴题.
【分析】本题是一个三角恒等变换问题,解题的关键是减小角的倍数,化异为同,利用方程的思想解题是三角函数常见的做法,最后是给值求角的问题,注意不要漏解.
【解答】解:∵cos2x=cosx+sinx,
∴cos2x﹣sin2x=cosx+sinx,
∴(cosx+sinx)(cosx﹣sinx)﹣(cosx+sinx)=0,
∴(cosx+sinx)(cosx﹣sinx﹣1)=0.
如果cosx+sinx=0,则得1+tgx=0,tgx=﹣1,
解
如果cosx+sinx﹣1=0则得cosx﹣sinx=1,
∴,∴,
∴,∴.
综上,x=.
【点评】本题是一个三角恒等变换问题,与初中学习锐角三角函数一样,高中也要研究同角三角函数之间关系,弄清同角各不同三角函数之间的联系,实现不同函数值之间的互相转化.
同课章节目录
