4.1 成比例线段(第2课时) 等比性质课件(21张PPT)2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 4.1 成比例线段(第2课时) 等比性质课件(21张PPT)2024-2025学年北师大版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
4.1 成比例线段
第四章 图形的相似
第2课时 等比性质
九年级上册数学(北师版)
复习导入
比例的基本性质:
四条线段 a,b,c,d 中,如果 a 与 b 的比等于 c 与 d 的比,即 ,那么这四条线段 a,b,c,d 叫做 ,简称 .
成比例线段
比例线段
如果 ,那么 ad = bc.
如果 ad = bc(a,b,c,d 都不等于 0),那么 .
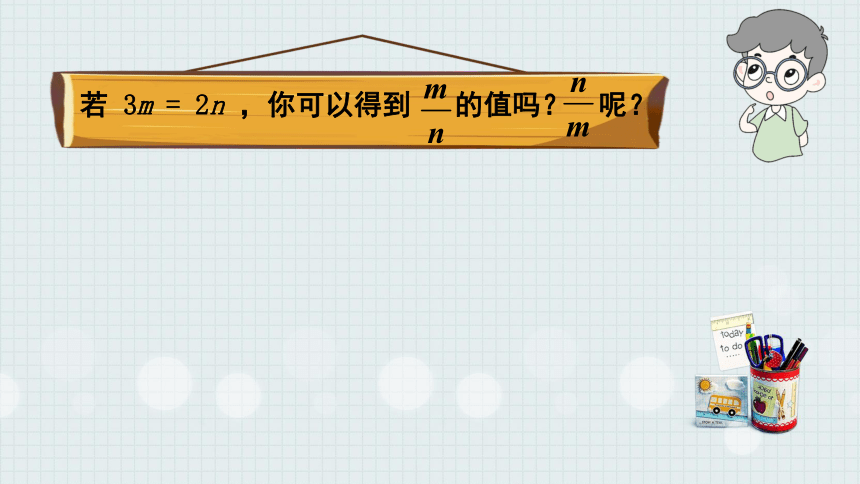
若 3m = 2n ,你可以得到 的值吗? 呢?
探究新知
1.如图已知 ,你能求出 与 的值吗?如果 ,那么 与 有怎么样
的关系?在求解过程中,你有什么发现?
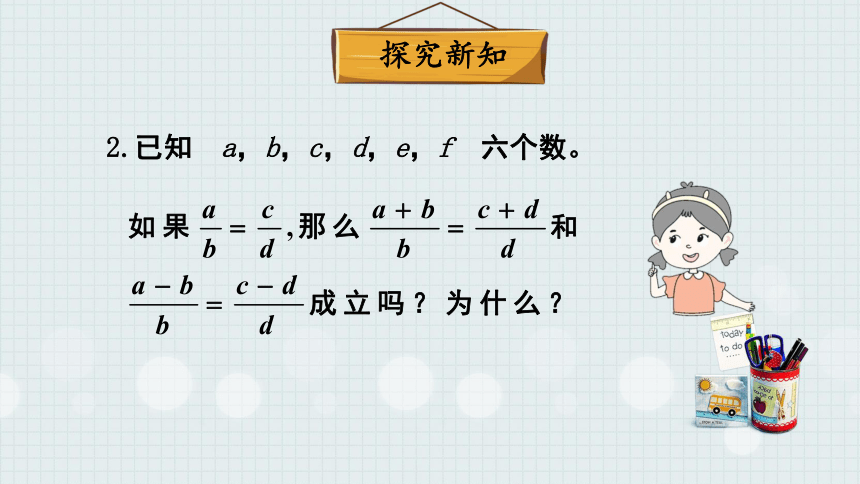
2.已知 a,b,c,d,e,f 六个数。
探究新知
等比性质
1
探究新知
问题:在图中,已知 ,
你能求出 的值吗?由此你能得出什么结论?
A
B
C
D
E
F
G
H
画图测量
已知 a,b,c,d,e,f 六个数,如果
(b + d + f ≠ 0),那么 成立吗?为什么?
设 ,则
a = kb,c = kd,e = kf .
所以
议一议
由此可得到比例的又一性质:
等比性质
比例的基本性质
例1 在 △ABC 与 △DEF 中,已知 ,且 △ABC 的周长为 18 cm,求 △DEF 的周长.
解:∵ ∴
∴4(AB + BC + CA) = 3(DE + EF + FD).
即 DE + EF + FD = (AB + BC + CA) .
又∵△ABC 的周长为 18 cm,即 AB + BC + CA = 18 cm.
∴△DEF 的周长为 24 cm.
例2 若 a,b,c 都是不等于零的数,且
求 k 的值.
得 ,则 k = 2.
当 a + b + c=0 时,则有 a + b = -c.
此时 .
综上所述,k 的值是 2 或-1.
解:当 a + b + c ≠ 0 时,由 ,
针对训练
1.已知 ,若 b + d + f = 9,则 a + c + e = ( )
A.12 B.15 C.16 D.1
∵ b + d + f = 9,
解析:
∴ a + c + e = .
A
典例精析
例3已知 ,则 的值为 .
解:设 ,
则 a = 2k,b = 3k,c = 5k .
1
…… 设元
…… 表示
…… 消元
1.(1)已知 ,那么 = , = .
(3)如果 ,那么 .
(2)如果 ,那么 .
课堂练习
2.已知四个数 a,b,c,d 成比例.
(1)若 a = -3,b = 9,c = 2,求 d;
(2)若 a = -3,b= ,c = 2,求 d.
解:
解:
, -3d=2, d= -
比例的
性质
如果 那么 ad = bc.
基本
性质
等比
性质
如果 ad = bc (a,b,c,d 都不等于 0),
那么
当堂小结
已知
= .
【选自教材P80 随堂练习 】
达标检测
达标检测
2. 已知 (b+d+f≠0) ,求 的值.
【选自教材P80 习题4.2】
如图,已知每个小方格的边长均为1,求AB,DE,
BC,DC,AC,EC的长,并计算△ABC与△EDC
的周长比.
【选自教材P80 习题4.2】
如果 ,那么 , . 你
认为这个结论正确吗?为什么?
【选自教材P80 习题4.2】
4.1 成比例线段
第四章 图形的相似
第2课时 等比性质
九年级上册数学(北师版)
复习导入
比例的基本性质:
四条线段 a,b,c,d 中,如果 a 与 b 的比等于 c 与 d 的比,即 ,那么这四条线段 a,b,c,d 叫做 ,简称 .
成比例线段
比例线段
如果 ,那么 ad = bc.
如果 ad = bc(a,b,c,d 都不等于 0),那么 .
若 3m = 2n ,你可以得到 的值吗? 呢?
探究新知
1.如图已知 ,你能求出 与 的值吗?如果 ,那么 与 有怎么样
的关系?在求解过程中,你有什么发现?
2.已知 a,b,c,d,e,f 六个数。
探究新知
等比性质
1
探究新知
问题:在图中,已知 ,
你能求出 的值吗?由此你能得出什么结论?
A
B
C
D
E
F
G
H
画图测量
已知 a,b,c,d,e,f 六个数,如果
(b + d + f ≠ 0),那么 成立吗?为什么?
设 ,则
a = kb,c = kd,e = kf .
所以
议一议
由此可得到比例的又一性质:
等比性质
比例的基本性质
例1 在 △ABC 与 △DEF 中,已知 ,且 △ABC 的周长为 18 cm,求 △DEF 的周长.
解:∵ ∴
∴4(AB + BC + CA) = 3(DE + EF + FD).
即 DE + EF + FD = (AB + BC + CA) .
又∵△ABC 的周长为 18 cm,即 AB + BC + CA = 18 cm.
∴△DEF 的周长为 24 cm.
例2 若 a,b,c 都是不等于零的数,且
求 k 的值.
得 ,则 k = 2.
当 a + b + c=0 时,则有 a + b = -c.
此时 .
综上所述,k 的值是 2 或-1.
解:当 a + b + c ≠ 0 时,由 ,
针对训练
1.已知 ,若 b + d + f = 9,则 a + c + e = ( )
A.12 B.15 C.16 D.1
∵ b + d + f = 9,
解析:
∴ a + c + e = .
A
典例精析
例3已知 ,则 的值为 .
解:设 ,
则 a = 2k,b = 3k,c = 5k .
1
…… 设元
…… 表示
…… 消元
1.(1)已知 ,那么 = , = .
(3)如果 ,那么 .
(2)如果 ,那么 .
课堂练习
2.已知四个数 a,b,c,d 成比例.
(1)若 a = -3,b = 9,c = 2,求 d;
(2)若 a = -3,b= ,c = 2,求 d.
解:
解:
, -3d=2, d= -
比例的
性质
如果 那么 ad = bc.
基本
性质
等比
性质
如果 ad = bc (a,b,c,d 都不等于 0),
那么
当堂小结
已知
= .
【选自教材P80 随堂练习 】
达标检测
达标检测
2. 已知 (b+d+f≠0) ,求 的值.
【选自教材P80 习题4.2】
如图,已知每个小方格的边长均为1,求AB,DE,
BC,DC,AC,EC的长,并计算△ABC与△EDC
的周长比.
【选自教材P80 习题4.2】
如果 ,那么 , . 你
认为这个结论正确吗?为什么?
【选自教材P80 习题4.2】
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
