安徽省合肥市第四十五中学2024-2025学年九年级上学期10月随堂练习数学试题(pdf版,无答案)
文档属性
| 名称 | 安徽省合肥市第四十五中学2024-2025学年九年级上学期10月随堂练习数学试题(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 19:23:38 | ||
图片预览


文档简介
随堂练习 2024.10.12
一.选择题(共 10 小题)
1.下列函数中,y是关于 x的二次函数的是( )
1
A.y=x+1 B. y 2 C.y=x(x﹣1) D.y=(x﹣1)2﹣x2x
2.抛物线 y=(x﹣2)2+1 图象的顶点坐标是( )
A.(- 2,1) B.(2,1) C. (﹣2,- 1) D.(2,- 1)
k
3.若点(3,4)在反比例函数 y 的图象上,则该图象也过点( )
x
A.(2,8) B.(4,2) C.(﹣3,- 4) D.(6,3)
4.抛物线 y=x2 的图象先向右平移 3 个单位,再向上平移 1 个单位,得到的新抛物
线的解析式为( )
A.y=(x﹣3)2+1 B.y=(x﹣3)2﹣1 C.y=(x+ 3)2+1 D.y=(x+ 3)2﹣1
5.对于抛物线 y=5x2 + 2 的说法不正确的是( )
A.开口向上 B.图象经过第一、二、三象限
C.函数最小值是 2 D.当 x<0 时,y随 x的增大而减小
6.下表是一组二次函数 y=x2+2x﹣4 的自变量 x与函数值 y的对应值:
x 1 1.1 1.2 1.3 1.4
y ﹣1 ﹣0.59 ﹣0.16 0.29 0.76
那么方程 x2+2x﹣4=0 的一个近似根是(精确到 0.1)( )
A. 1.1 B.1.2 C.1.3 D.1.4
7.设 A(- 2,y1),B( 1 , y2), C( 3 ,y3)是抛物线 y (x 1)2 k 上的三点,则( )
A. y3 y2 y1 B. y3 y1 y2 C. y2 y1 y3 D. y1 y2 y3
8.飞机着陆后滑行的距离 s(单位:m)与滑行的时间 t(单位:s)的函数解析式
是 s=40t﹣t2,那么飞机着陆后滑行多长时间才能停下来?( )
A.20s B.40s C.60s D.80s
9.某商家代销一种产品,销售中发现每件售价 99 元时,日销售量为 200 件,当每
件产品下降 1 元时,日销售量增加 2 件.已知每售出 1 件产品,该商家需支付厂
家和其他费用共 50 元,设每件产品售价为 x(元),商家每天的利润为 w(元),
则 w与 x之间的函数解析式为( )
A.w=(99﹣x)[200+2(x﹣50)] B.w=(99﹣x)[200+2(50﹣x)]
C.w=(x﹣50)[200+2(x﹣99)] D.w=(x﹣50)[200+2(99﹣x)]
10.抛物线 y=ax2+bx+c(a,b,c是常数,a<0)经过(﹣1,1),(m,1)两点,
且 0<m<1.下列四个结论:
①b <0;②若 0<x<1,则 a(x﹣1)2+b(x﹣1)+c>1;
③若 a=﹣1,则关于 x的一元二次方程 ax2+bx+c=2 无实数解;
④点 A(x1,y1),B(x 12,y2)在抛物线上,若 x1+x2>﹣ ,x1>x2,总有 y1<
2
y 12,则 0<m≤ .其中正确的有( )个.
2
A.1 B.2 C.3 D.4
1
{#{QQABAQQSAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkkJAIhALAegAMSgBOVhCENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
二.填空题(共 4 小题)
k
11.在反比例函数 y 的每一个分支上,y都随 x的增大而减小,则 k的取值范围
x
是 .
12. 二次函数 y=(x - 1)(x - 3)的对称轴是直线 .
k
13. 如图,矩形 ABCD的顶点 A和对称中心在反比例函数 y (k≠0,x<0)的图
x
象上,若矩形 ABCD的面积为 12,则 k的值为 .
14.在平面直角坐标系中,A点坐标为(﹣1,﹣2),B点坐标为(5,4).
(1)若抛物线 y=x2﹣2x+c经过点 A,则 c的值为 .
(2)若抛物线 y= x2﹣2x+c 与线段 AB 只有一个公共点,则 c 的取值范围
为 .
第 13 题 第 14题
三.解答题(共 9 小题)
15.已知关于 x的二次函数的图象的顶点坐标为(﹣2,- 3),且图象过点(0,1),
求这个二次函数的解析式.
16.二次函数 y=ax2+bx+c的图象如图所示,求该函数的解析式.
2
{#{QQABAQQSAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkkJAIhALAegAMSBgOVhCENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
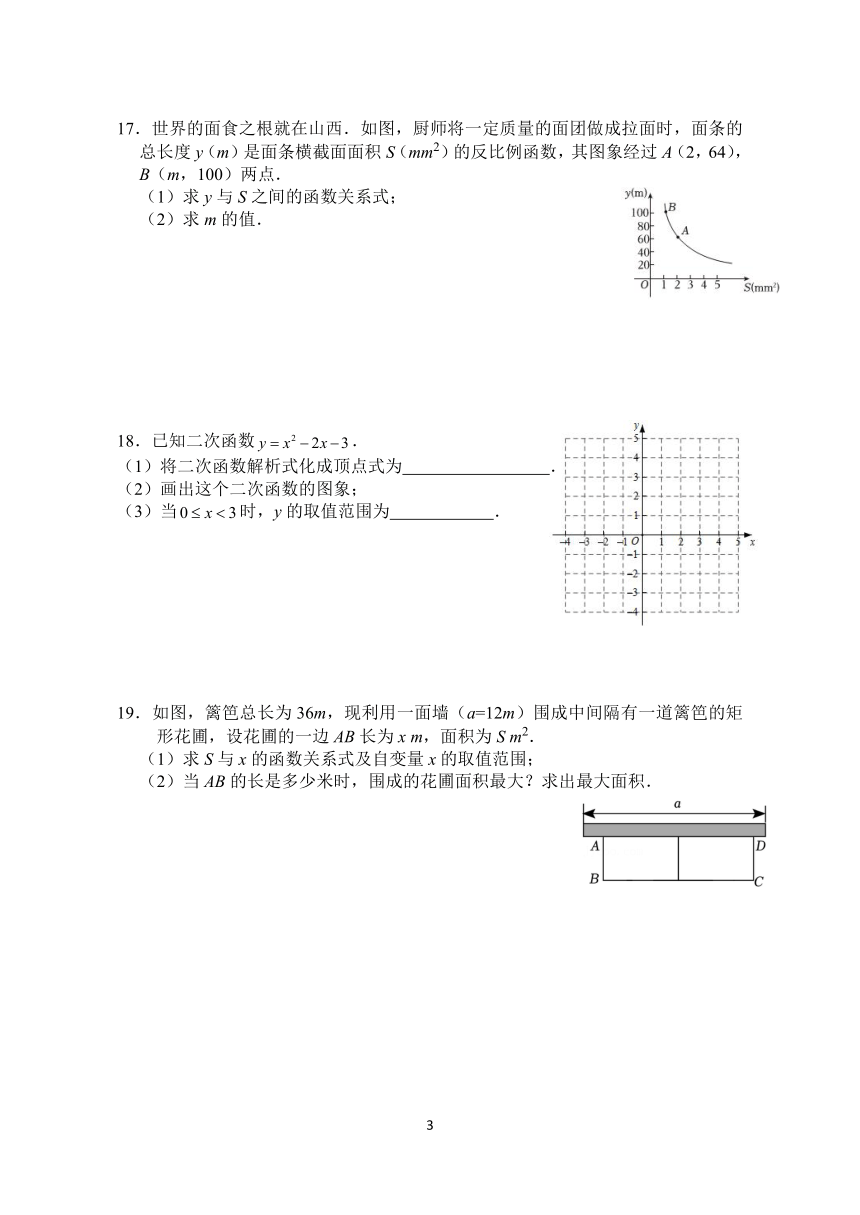
17.世界的面食之根就在山西.如图,厨师将一定质量的面团做成拉面时,面条的
总长度 y(m)是面条横截面面积 S(mm2)的反比例函数,其图象经过 A(2,64),
B(m,100)两点.
(1)求 y与 S之间的函数关系式;
(2)求 m的值.
18.已知二次函数 y x2 2x 3.
(1)将二次函数解析式化成顶点式为 .
(2)画出这个二次函数的图象;
(3)当0 x 3时,y的取值范围为 .
19.如图,篱笆总长为 36m,现利用一面墙(a=12m)围成中间隔有一道篱笆的矩
形花圃,设花圃的一边 AB长为 x m,面积为 S m2.
(1)求 S与 x的函数关系式及自变量 x的取值范围;
(2)当 AB的长是多少米时,围成的花圃面积最大?求出最大面积.
3
{#{QQABAQSQAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkJkIAhALAegAMSgBOVhCENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
20.如图,在平面直角坐标系中,一次函数 y=ax+b(a<0)与反比例函数 y= (k
≠0)交于 A(﹣m,3m),B(4,﹣3)两点,与 y轴交于点 C,连接 OA,OB.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
k
(3)请根据图象直接写出不等式 ax b的解集.
x
21.如图,隧道的截面由抛物线和矩形 OABC构成,OA=8m,OC=2m,抛物线的最
高点到路面的距离为 6 米.
(1)按如图所示建立平面直角坐标系,求该抛物线的函数表达式;
(2)一辆货运卡车高为 4m,宽为 2m,如果该隧道内设双向车道,那么这辆货
车能否安全通过?
4
{#{QQABAQQSAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkkJIAhALAegAMSBgOVChENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
22.如图,已知抛物线 y=﹣x2+bx+c与直线相交于 A(﹣1,0),C(2,3).
(1)抛物线及直线 AC的函数关系式;
(2)如图 1,若 P是抛物线上位于直线 AC上方的一个动点,求△APC的面积最
大值;
(3)如图 2,若 P是抛物线上的一个动点,PQ⊥x轴交 AC于点 Q,若 C是
等腰直角三角形,则点 P的坐标为________________________________.
图 1 图 2
5
{#{QQABAQSQAs5oggioYAkIIASAACQQh5CqUw0WuKCwgiCQQkJkIAhALAegAMSgBOVChENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
23.某药厂销售部门根据市场调研结果,对该厂生产的一种新型药品未来两年的销
售进行预测,发现月销售量 P (吨)与 t (月)的函数关系式如下:
k (0 t 8)
P t 4
mt n (8 t 24)
(1)根据图象求 P与 t的函数关系式;
(2)预测月销量不低于 15 吨有_________个月;
(3)若该药品每吨的利润 Q (万元)与 t (月)之间满足如下关系:
2t 8 (0 t 12)
Q 预测药厂未来两年的月最大利润.
t 44 (12 t 24) .
6
{#{QQABAQSQAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkJkAIhALAegAMSBgOVChENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
一.选择题(共 10 小题)
1.下列函数中,y是关于 x的二次函数的是( )
1
A.y=x+1 B. y 2 C.y=x(x﹣1) D.y=(x﹣1)2﹣x2x
2.抛物线 y=(x﹣2)2+1 图象的顶点坐标是( )
A.(- 2,1) B.(2,1) C. (﹣2,- 1) D.(2,- 1)
k
3.若点(3,4)在反比例函数 y 的图象上,则该图象也过点( )
x
A.(2,8) B.(4,2) C.(﹣3,- 4) D.(6,3)
4.抛物线 y=x2 的图象先向右平移 3 个单位,再向上平移 1 个单位,得到的新抛物
线的解析式为( )
A.y=(x﹣3)2+1 B.y=(x﹣3)2﹣1 C.y=(x+ 3)2+1 D.y=(x+ 3)2﹣1
5.对于抛物线 y=5x2 + 2 的说法不正确的是( )
A.开口向上 B.图象经过第一、二、三象限
C.函数最小值是 2 D.当 x<0 时,y随 x的增大而减小
6.下表是一组二次函数 y=x2+2x﹣4 的自变量 x与函数值 y的对应值:
x 1 1.1 1.2 1.3 1.4
y ﹣1 ﹣0.59 ﹣0.16 0.29 0.76
那么方程 x2+2x﹣4=0 的一个近似根是(精确到 0.1)( )
A. 1.1 B.1.2 C.1.3 D.1.4
7.设 A(- 2,y1),B( 1 , y2), C( 3 ,y3)是抛物线 y (x 1)2 k 上的三点,则( )
A. y3 y2 y1 B. y3 y1 y2 C. y2 y1 y3 D. y1 y2 y3
8.飞机着陆后滑行的距离 s(单位:m)与滑行的时间 t(单位:s)的函数解析式
是 s=40t﹣t2,那么飞机着陆后滑行多长时间才能停下来?( )
A.20s B.40s C.60s D.80s
9.某商家代销一种产品,销售中发现每件售价 99 元时,日销售量为 200 件,当每
件产品下降 1 元时,日销售量增加 2 件.已知每售出 1 件产品,该商家需支付厂
家和其他费用共 50 元,设每件产品售价为 x(元),商家每天的利润为 w(元),
则 w与 x之间的函数解析式为( )
A.w=(99﹣x)[200+2(x﹣50)] B.w=(99﹣x)[200+2(50﹣x)]
C.w=(x﹣50)[200+2(x﹣99)] D.w=(x﹣50)[200+2(99﹣x)]
10.抛物线 y=ax2+bx+c(a,b,c是常数,a<0)经过(﹣1,1),(m,1)两点,
且 0<m<1.下列四个结论:
①b <0;②若 0<x<1,则 a(x﹣1)2+b(x﹣1)+c>1;
③若 a=﹣1,则关于 x的一元二次方程 ax2+bx+c=2 无实数解;
④点 A(x1,y1),B(x 12,y2)在抛物线上,若 x1+x2>﹣ ,x1>x2,总有 y1<
2
y 12,则 0<m≤ .其中正确的有( )个.
2
A.1 B.2 C.3 D.4
1
{#{QQABAQQSAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkkJAIhALAegAMSgBOVhCENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
二.填空题(共 4 小题)
k
11.在反比例函数 y 的每一个分支上,y都随 x的增大而减小,则 k的取值范围
x
是 .
12. 二次函数 y=(x - 1)(x - 3)的对称轴是直线 .
k
13. 如图,矩形 ABCD的顶点 A和对称中心在反比例函数 y (k≠0,x<0)的图
x
象上,若矩形 ABCD的面积为 12,则 k的值为 .
14.在平面直角坐标系中,A点坐标为(﹣1,﹣2),B点坐标为(5,4).
(1)若抛物线 y=x2﹣2x+c经过点 A,则 c的值为 .
(2)若抛物线 y= x2﹣2x+c 与线段 AB 只有一个公共点,则 c 的取值范围
为 .
第 13 题 第 14题
三.解答题(共 9 小题)
15.已知关于 x的二次函数的图象的顶点坐标为(﹣2,- 3),且图象过点(0,1),
求这个二次函数的解析式.
16.二次函数 y=ax2+bx+c的图象如图所示,求该函数的解析式.
2
{#{QQABAQQSAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkkJAIhALAegAMSBgOVhCENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
17.世界的面食之根就在山西.如图,厨师将一定质量的面团做成拉面时,面条的
总长度 y(m)是面条横截面面积 S(mm2)的反比例函数,其图象经过 A(2,64),
B(m,100)两点.
(1)求 y与 S之间的函数关系式;
(2)求 m的值.
18.已知二次函数 y x2 2x 3.
(1)将二次函数解析式化成顶点式为 .
(2)画出这个二次函数的图象;
(3)当0 x 3时,y的取值范围为 .
19.如图,篱笆总长为 36m,现利用一面墙(a=12m)围成中间隔有一道篱笆的矩
形花圃,设花圃的一边 AB长为 x m,面积为 S m2.
(1)求 S与 x的函数关系式及自变量 x的取值范围;
(2)当 AB的长是多少米时,围成的花圃面积最大?求出最大面积.
3
{#{QQABAQSQAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkJkIAhALAegAMSgBOVhCENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
20.如图,在平面直角坐标系中,一次函数 y=ax+b(a<0)与反比例函数 y= (k
≠0)交于 A(﹣m,3m),B(4,﹣3)两点,与 y轴交于点 C,连接 OA,OB.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
k
(3)请根据图象直接写出不等式 ax b的解集.
x
21.如图,隧道的截面由抛物线和矩形 OABC构成,OA=8m,OC=2m,抛物线的最
高点到路面的距离为 6 米.
(1)按如图所示建立平面直角坐标系,求该抛物线的函数表达式;
(2)一辆货运卡车高为 4m,宽为 2m,如果该隧道内设双向车道,那么这辆货
车能否安全通过?
4
{#{QQABAQQSAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkkJIAhALAegAMSBgOVChENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
22.如图,已知抛物线 y=﹣x2+bx+c与直线相交于 A(﹣1,0),C(2,3).
(1)抛物线及直线 AC的函数关系式;
(2)如图 1,若 P是抛物线上位于直线 AC上方的一个动点,求△APC的面积最
大值;
(3)如图 2,若 P是抛物线上的一个动点,PQ⊥x轴交 AC于点 Q,若 C是
等腰直角三角形,则点 P的坐标为________________________________.
图 1 图 2
5
{#{QQABAQSQAs5oggioYAkIIASAACQQh5CqUw0WuKCwgiCQQkJkIAhALAegAMSgBOVChENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
23.某药厂销售部门根据市场调研结果,对该厂生产的一种新型药品未来两年的销
售进行预测,发现月销售量 P (吨)与 t (月)的函数关系式如下:
k (0 t 8)
P t 4
mt n (8 t 24)
(1)根据图象求 P与 t的函数关系式;
(2)预测月销量不低于 15 吨有_________个月;
(3)若该药品每吨的利润 Q (万元)与 t (月)之间满足如下关系:
2t 8 (0 t 12)
Q 预测药厂未来两年的月最大利润.
t 44 (12 t 24) .
6
{#{QQABAQSQAs5oggioYAkIIASAACQQh5CqUw0WuKCwgCiQQkJkAIhALAegAMSBgOVChENAKAMRACAiJAFCARBFKAB=C}#A}=}#}
同课章节目录
