4.4 第1课时 利用两角判定三角形相似 课件(共39张PPT) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 4.4 第1课时 利用两角判定三角形相似 课件(共39张PPT) 2024-2025学年北师大版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 22:29:13 | ||
图片预览





文档简介
(共39张PPT)
4.4 探索三角形相似的条件
第四章 图形的相似
第1课时 利用两角判定三角形相似
九年级上册数学(北师版)
问题1 这两个三角形有什么关系?
全等三角形
情境导入
那这样变化一下呢?
相似三角形
相似三角形定义:我们把三角分别相等、三边成比例的两个三角形叫做相似三角形.
对应角……?
对应边……?
问题2 根据相似多边形的定义,你能说说什么叫相似三角形吗?
全等是一种特殊的相似
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
角边角
ASA
角角边
AAS
边边边
SSS
边角边
SAS
斜边、直角边
HL
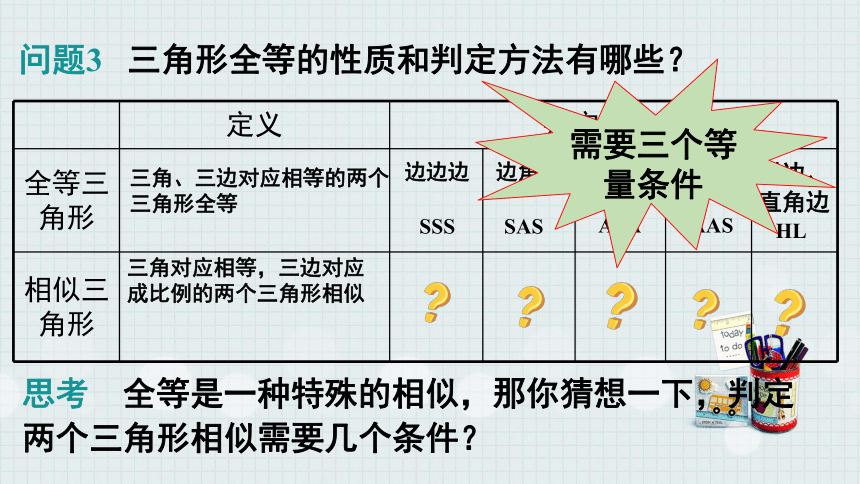
问题3 三角形全等的性质和判定方法有哪些?
需要三个等量条件
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
相似多边形
各角分别相等、各边成比例
相似三角形
三角分别相等、三边成比例
类比引入
可否用比较少的条件来判定三角形相似呢?
类比全等三角形
全等三角形
复习回顾
全等三角形
对应边相等,对应角相等
[——北师版 七年级 数学下册 教材P93、P98、P101、P103]
① 一个条件
② 两个条件
③ 三个条件
①
SSS
②
ASA
③
AAS
④
SAS
返回
探究新知
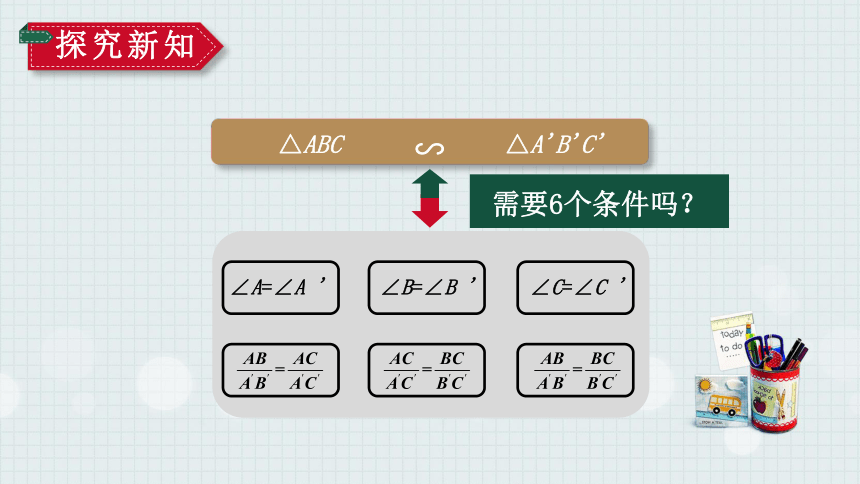
∽
△ABC
△A'B'C'
∠A=∠A '
∠B=∠B '
∠C=∠C '
需要6个条件吗?
探究新知
∽
△ABC
△A'B'C'
∠A=∠A '
∠B=∠B '
∠C=∠C '
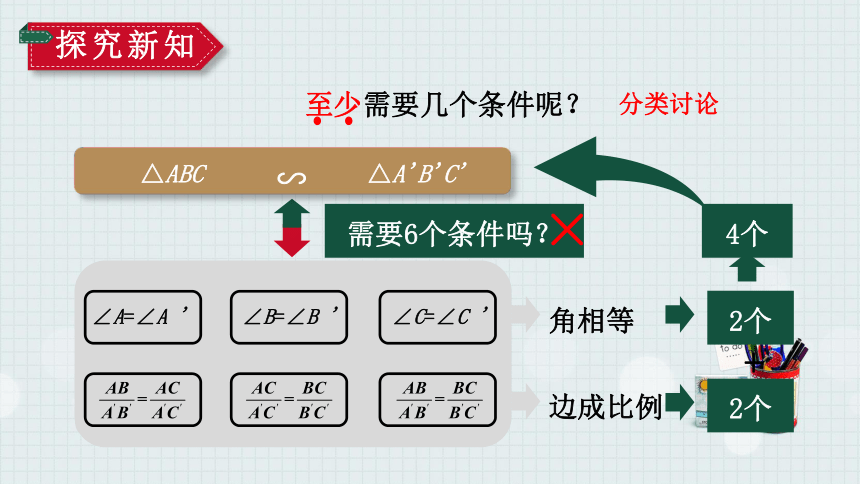
需要6个条件吗?
角相等
边成比例
2个
2个
+
4个
至少需要几个条件呢?
分类讨论
想一想
(1) 一个条件
①一个角相等
②两边成比例
只有一个角相等,
两个三角形相似吗?
只有两边成比例,
两个三角形相似吗?
A
B
C
A'
B'
C'
A
B
C
A'
B'
C'
反例:
反例:
C
A
B
A'
B'
C'
如果两个三角形只有一个角相等,它们一定相似吗?
如果两个三角形只有一个角相等,它们不一定相似.
探究新知
两角分别相等的两个三角形相似
1
想一想
如果有两个角分别相等呢?
想一想
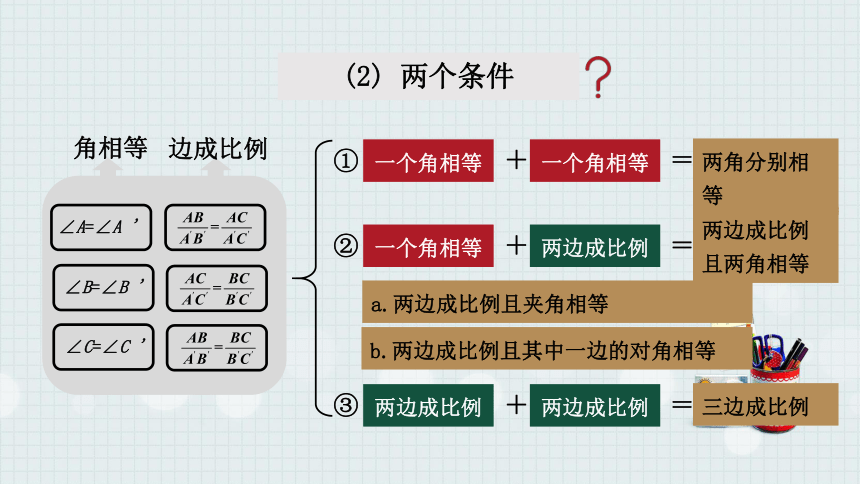
(2) 两个条件
有哪几种情况呢?
∠A=∠A '
∠B=∠B '
∠C=∠C '
角相等
边成比例
(2) 两个条件
①
一个角相等
一个角相等
+
=
两角分别相等
②
一个角相等
两边成比例
+
=
两边成比例且两角相等
③
两边成比例
两边成比例
+
=
三边成比例
a.两边成比例且夹角相等
b.两边成比例且其中一边的对角相等
(2) 两个条件
①
一个角相等
+
=
两角分别相等
一个角相等
做一做
与同伴合作,两个人分别画△ABC和△A′B′C′,
使得∠A=∠A′=∠α,∠B=∠B′=∠β;
那么三边的比 相等吗?
这样的两个三角形相似吗?
与同伴合作,两个人分别画 △ABC 和 △A'B'C',使得∠A 和 ∠A' 都等于∠α,∠B 和 ∠B' 都等于 ∠β,此时, ∠C 与 ∠C' 相等吗?三边的比 相等吗?这样的两个三角形相似吗?
改变 ∠α,∠β 的大小,再试一试.
合作探究
这两个三角形是相似的
A'
B'
C'
C
A
B
证明:在 △ABC 的边 AB(或 AB 的延长线)上,
截取 AD = A′B′,过点 D 作 DE//BC,交 AC 于点 E,则有 △ADE ∽△ABC,∠ADE =∠B.
∵∠B =∠B′,
∴∠ADE =∠B′.
又∵ AD = A′B′,∠A =∠A′,
∴△ADE ≌△A′B′C′.
∴△A′B′C′ ∽△ABC.
D
E
验证:试证明 △A′B′C′∽△ABC.
A'
B'
C'
C
A
B
判定定理 1
定理 两角分别相等的两个三角形相似
在△ABC 和△A'B'C'中,
如果∠A=∠A',∠B= ∠B',
那么△ABC∽△A'B'C'
A
B
C
A'
C'
B'
数学语言:
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵ ∠A =∠A',∠B =∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
归纳总结
A'
B'
C'
C
A
B
例1 如图,D、E 分别是 △ABC 的边 AB,AC 上的点,DE∥BC, AB = 7,AD = 5,DE = 10,求BC 的长.
解:∵DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴△ADE∽△ABC.
(两角分别相等的两个三角形相似).
∴ ,即 . ∴BC = 14.
B
A
D
E
C
典例精析
如图,△ABC 中,DE∥BC,EF∥AB,求证:
△ADE∽△EFC.
A
E
F
B
C
D
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
练一练
证明:∵∠BAC = ∠1+∠DAC,∠DAE = ∠3 +∠DAC,∠1=∠3,
∴ ∠BAC = ∠DAE.
∵∠C = 180°-∠2-∠DOC ,
∠E = 180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C =∠E.(“8”字模型)
∴ △ABC∽△ADE.
例2 如图,∠1 =∠2 =∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
图a
b,
图b
图a
图b
图c
图d
a
a,b,c)
d)
∴
解:∵ ED⊥AB,∴∠EDA = 90°.
又∠C = 90°,∠A =∠A,
∴ △AED ∽△ABC.
例3 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为 D. 求 AD 的长.
D
A
B
C
E
∴
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
1. 如图,已知 AB∥DE,∠AFC =∠E,则图中相
似三角形共有( )
A. 1对 B. 2对
C. 3对 D. 4对
C
课堂练习
2. 如图,点 D 在 AB上,当∠ =
∠ (或∠ =∠ )时,△ACD∽△ABC.
A
B
D
C
ACD
ACB
B
ADC
3. 如图,在△ABC 中,AE 交 BC 于点 D,∠C = ∠E,AD : DE = 3 : 5,AE = 8,BD = 4,则 DC 的长等于 ( )
A.
B.
C.
D.
A
C
A
B
D
E
证明:∵ 在△ABC 中,∠A = 40°,∠B = 80°,
∴ ∠C = 180°-∠A-∠B = 60°.
∵ 在△DEF 中,∠E = 80°,∠F = 60°,
∴ ∠B = ∠E,∠C = ∠F.
∴ △ABC ∽△DEF.
4. 如图,在△ABC 和 △DEF 中,∠A = 40°,∠B = 80°,∠E = 80°,∠F = 60°.求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明: ∵ △ABC 的高 AD、BE 交于点 F,
∴ ∠FEA = ∠FDB = 90°.
又∵∠AFE =∠BFD (对顶角相等),
5. 如图,△ABC 的高 AD、BE 交于点 F.求证:
D
C
A
B
E
F
∴ △FEA ∽ △ FDB.
∴
利用两角判定三角形相似
定理1:两角分别相等的两个三角形相似
相似三角形的判定定理 1 的运用
当堂小结
【选自教材P90 随堂练习】
1.有一个锐角相等的两个直角三角形是否相似?为什么?
2.顶角相等的两个等腰三角形是否相似?为什么?
相似,理由是:直角相等,一锐角相等,即有两角分别相等,根据“两角分别相等的两个三角形相似”可知这两个三角形相似.
相似,理由是:因为顶角相等,两个底角也分别相等.
随堂练习
【选自教材P90 习题4.5 第1题】
1.在△ABC与△DEF中,∠A=∠D=70°,∠B=60°,∠E=50°,
这两个三角形相似吗?为什么?
解:相似.
根据三角形内角和定理,
可得∠C=50°,即∠C=∠E,
又已知∠A=∠D,
所以△ABC∽△DEF.
巩固练习
【选自教材P90 习题4.5 第2题】
2.如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.
找出图中的相似三角形,并说明理由.
A
B
C
D
O
解:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC
∴△ABO∽△CDO.
A
B
C
D
解(1)△ABC∽△DBA,
△ABC∽△DAC,
△DBA∽△DAC,
3.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出AD2=BD·DC吗?
【选自教材P90 习题4.5 第3题】
3.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出AD2=BD·DC吗?
A
B
C
D
解:(2)能得出AD2=BD·DC.
理由如下:
由(1)可知△DBA∽△DAC,
∴
即
AD2=BD·DC.
【选自教材P90 习题4.5 第3题】
4.将两个全等的等腰直角三角形摆成如图所示的样子,(图中的所有点、线都在同一平面内),请在图中找出两对相似而不全等的三角形,并说明它们相似的理由.
A
B
C
D
E
F
G
解:△ABE∽△DAE.
理由:∠BEA=∠AED,
∠B=∠DAE=45°,
△ADC∽△EDA.
理由:∠CDA=∠ADE,
∠DCA=∠DAE=45°.
【选自教材P90 习题4.5 第4题】
5.如图,为了测量一个大峡谷的宽度,位于峡谷一侧的地质勘探人员在对面的岩石上观察一个特别明显的标志点O,再在他们所在这一侧选点A、B、D,使得AB⊥AO,DB⊥AB,然后确定DO和AB的交点C.测得AC=120m,CB=60m,BD=50m,你能帮助他们算出峡谷的宽AO吗?
解:由AB⊥AO,DB⊥AB,
得∠OAC=∠DBC=90°,
又∠ACO=∠BCD,
所以△ACO∽△BCD.
∴
A
O
C
B
D
【选自教材P91 习题4.5 第5题】
两千六百多年前,埃及有个国王,想知道已经给他盖好了的大金字塔的确实高度,于是,命令祭司们去丈量。可是,没有一个祭司知道该怎样测量,在这个问题面前,祭司们个个束手无策。显然,人是不可能爬到那么高大的塔顶上去的;即使爬上去了,由于塔身是斜的,又怎样来测量呢?一时,金字塔的高度成了一个难题。同时悬赏求解答。
趣味拓展
有一个叫法涅斯的学者,看到国王的诏书后,决心解决这个难题。他想了好几个解题的方案,但都行不通。失败并没有使他灰心。法涅斯索性来到外面,一边踱步,一边思索解决的办法,以致撞到树上。于是,他转了个弯,又走下去。太阳把他的影子投到地上,他走到那里,影子也跟到哪里。这时,他突然看到自己的影子,于是想:是不是可以请太阳来帮忙呢?在古埃及人的眼里,太阳是万能的,太阳能给人温暖,能帮助人们确定方向。法涅斯眼前一亮,他清楚记得,早上和傍晚每个物体都拖着一个长长的影子,而中午每个物体的影子都很短……那么,是不是有一个时刻,物体的影子就等于物体的高度呢?他自言自语起来。
想到这里,法涅斯就找了一根竿子,竖在太阳底下,认真观察、测量起来。经过几天的观察、测量,法涅斯终于证实了自己的想法一有一个时候,物体的影子等于物体的高度。于是,他去测量好金字塔底边的长度,并把数据记下来。然后,他毫不犹豫地揭下了悬挂的诏书。国王得到“有人揭下招字” 的报告后,高兴万分,派人把法涅斯召进王官,盛情款待.一切准备停当后,国王选择了一个风和日丽的日子,举行测塔仪式。测塔这天,国王在祭司们的陪同下,和法涅斯一起来到金字塔旁。看热闹的人黑压压一片,喧哗奢,拥挤著,他们等待著庄严的一刻到来。法涅斯站在测塔指挥台上,俨然像个天使,一动也不动地注视著自己的影子。
看看时间快到了,太阳光给每一个在场的人和巨大的金字塔都投下了黑黑的影子。当法涅斯确定他自己的影子已等于他的身高时,便发出了测塔的命令。这时,助手们立即测出了金字塔的阴影的长。接着,法涅斯十分准确地算出了金字塔的高度,最后,他还把测量金字塔高度的秘密告诉大家。场上,发出一阵热烈的欢呼声。显然,法涅斯利用相似三角形的原理测得了塔高。在法涅斯以前,还没有人知道这个原理呢!法涅斯第一次发现、利用这个原理。在那个时代,这是一个伟大的创举!
在这个基础上,法涅斯进一步研究,得出一个法则:在任意两个对应角相等的三角形中,对应边的比率也相等。从而,找到了在任何季节,在任何时候都能测塔高的方法。
①两角分别相等
③两边成比例且其中一边的对角相等
②两边成比例且夹角相等
④三边成比例
课堂小结
(2) 两个条件
①只有一个角相等
②只有两边成比例
类比
分类
两个三角形
相似至少需要
几个条件呢?
(1) 一个条件
4.4 探索三角形相似的条件
第四章 图形的相似
第1课时 利用两角判定三角形相似
九年级上册数学(北师版)
问题1 这两个三角形有什么关系?
全等三角形
情境导入
那这样变化一下呢?
相似三角形
相似三角形定义:我们把三角分别相等、三边成比例的两个三角形叫做相似三角形.
对应角……?
对应边……?
问题2 根据相似多边形的定义,你能说说什么叫相似三角形吗?
全等是一种特殊的相似
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
角边角
ASA
角角边
AAS
边边边
SSS
边角边
SAS
斜边、直角边
HL
问题3 三角形全等的性质和判定方法有哪些?
需要三个等量条件
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
相似多边形
各角分别相等、各边成比例
相似三角形
三角分别相等、三边成比例
类比引入
可否用比较少的条件来判定三角形相似呢?
类比全等三角形
全等三角形
复习回顾
全等三角形
对应边相等,对应角相等
[——北师版 七年级 数学下册 教材P93、P98、P101、P103]
① 一个条件
② 两个条件
③ 三个条件
①
SSS
②
ASA
③
AAS
④
SAS
返回
探究新知
∽
△ABC
△A'B'C'
∠A=∠A '
∠B=∠B '
∠C=∠C '
需要6个条件吗?
探究新知
∽
△ABC
△A'B'C'
∠A=∠A '
∠B=∠B '
∠C=∠C '
需要6个条件吗?
角相等
边成比例
2个
2个
+
4个
至少需要几个条件呢?
分类讨论
想一想
(1) 一个条件
①一个角相等
②两边成比例
只有一个角相等,
两个三角形相似吗?
只有两边成比例,
两个三角形相似吗?
A
B
C
A'
B'
C'
A
B
C
A'
B'
C'
反例:
反例:
C
A
B
A'
B'
C'
如果两个三角形只有一个角相等,它们一定相似吗?
如果两个三角形只有一个角相等,它们不一定相似.
探究新知
两角分别相等的两个三角形相似
1
想一想
如果有两个角分别相等呢?
想一想
(2) 两个条件
有哪几种情况呢?
∠A=∠A '
∠B=∠B '
∠C=∠C '
角相等
边成比例
(2) 两个条件
①
一个角相等
一个角相等
+
=
两角分别相等
②
一个角相等
两边成比例
+
=
两边成比例且两角相等
③
两边成比例
两边成比例
+
=
三边成比例
a.两边成比例且夹角相等
b.两边成比例且其中一边的对角相等
(2) 两个条件
①
一个角相等
+
=
两角分别相等
一个角相等
做一做
与同伴合作,两个人分别画△ABC和△A′B′C′,
使得∠A=∠A′=∠α,∠B=∠B′=∠β;
那么三边的比 相等吗?
这样的两个三角形相似吗?
与同伴合作,两个人分别画 △ABC 和 △A'B'C',使得∠A 和 ∠A' 都等于∠α,∠B 和 ∠B' 都等于 ∠β,此时, ∠C 与 ∠C' 相等吗?三边的比 相等吗?这样的两个三角形相似吗?
改变 ∠α,∠β 的大小,再试一试.
合作探究
这两个三角形是相似的
A'
B'
C'
C
A
B
证明:在 △ABC 的边 AB(或 AB 的延长线)上,
截取 AD = A′B′,过点 D 作 DE//BC,交 AC 于点 E,则有 △ADE ∽△ABC,∠ADE =∠B.
∵∠B =∠B′,
∴∠ADE =∠B′.
又∵ AD = A′B′,∠A =∠A′,
∴△ADE ≌△A′B′C′.
∴△A′B′C′ ∽△ABC.
D
E
验证:试证明 △A′B′C′∽△ABC.
A'
B'
C'
C
A
B
判定定理 1
定理 两角分别相等的两个三角形相似
在△ABC 和△A'B'C'中,
如果∠A=∠A',∠B= ∠B',
那么△ABC∽△A'B'C'
A
B
C
A'
C'
B'
数学语言:
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵ ∠A =∠A',∠B =∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
归纳总结
A'
B'
C'
C
A
B
例1 如图,D、E 分别是 △ABC 的边 AB,AC 上的点,DE∥BC, AB = 7,AD = 5,DE = 10,求BC 的长.
解:∵DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴△ADE∽△ABC.
(两角分别相等的两个三角形相似).
∴ ,即 . ∴BC = 14.
B
A
D
E
C
典例精析
如图,△ABC 中,DE∥BC,EF∥AB,求证:
△ADE∽△EFC.
A
E
F
B
C
D
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
练一练
证明:∵∠BAC = ∠1+∠DAC,∠DAE = ∠3 +∠DAC,∠1=∠3,
∴ ∠BAC = ∠DAE.
∵∠C = 180°-∠2-∠DOC ,
∠E = 180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C =∠E.(“8”字模型)
∴ △ABC∽△ADE.
例2 如图,∠1 =∠2 =∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
图a
b,
图b
图a
图b
图c
图d
a
a,b,c)
d)
∴
解:∵ ED⊥AB,∴∠EDA = 90°.
又∠C = 90°,∠A =∠A,
∴ △AED ∽△ABC.
例3 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为 D. 求 AD 的长.
D
A
B
C
E
∴
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
1. 如图,已知 AB∥DE,∠AFC =∠E,则图中相
似三角形共有( )
A. 1对 B. 2对
C. 3对 D. 4对
C
课堂练习
2. 如图,点 D 在 AB上,当∠ =
∠ (或∠ =∠ )时,△ACD∽△ABC.
A
B
D
C
ACD
ACB
B
ADC
3. 如图,在△ABC 中,AE 交 BC 于点 D,∠C = ∠E,AD : DE = 3 : 5,AE = 8,BD = 4,则 DC 的长等于 ( )
A.
B.
C.
D.
A
C
A
B
D
E
证明:∵ 在△ABC 中,∠A = 40°,∠B = 80°,
∴ ∠C = 180°-∠A-∠B = 60°.
∵ 在△DEF 中,∠E = 80°,∠F = 60°,
∴ ∠B = ∠E,∠C = ∠F.
∴ △ABC ∽△DEF.
4. 如图,在△ABC 和 △DEF 中,∠A = 40°,∠B = 80°,∠E = 80°,∠F = 60°.求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明: ∵ △ABC 的高 AD、BE 交于点 F,
∴ ∠FEA = ∠FDB = 90°.
又∵∠AFE =∠BFD (对顶角相等),
5. 如图,△ABC 的高 AD、BE 交于点 F.求证:
D
C
A
B
E
F
∴ △FEA ∽ △ FDB.
∴
利用两角判定三角形相似
定理1:两角分别相等的两个三角形相似
相似三角形的判定定理 1 的运用
当堂小结
【选自教材P90 随堂练习】
1.有一个锐角相等的两个直角三角形是否相似?为什么?
2.顶角相等的两个等腰三角形是否相似?为什么?
相似,理由是:直角相等,一锐角相等,即有两角分别相等,根据“两角分别相等的两个三角形相似”可知这两个三角形相似.
相似,理由是:因为顶角相等,两个底角也分别相等.
随堂练习
【选自教材P90 习题4.5 第1题】
1.在△ABC与△DEF中,∠A=∠D=70°,∠B=60°,∠E=50°,
这两个三角形相似吗?为什么?
解:相似.
根据三角形内角和定理,
可得∠C=50°,即∠C=∠E,
又已知∠A=∠D,
所以△ABC∽△DEF.
巩固练习
【选自教材P90 习题4.5 第2题】
2.如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.
找出图中的相似三角形,并说明理由.
A
B
C
D
O
解:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC
∴△ABO∽△CDO.
A
B
C
D
解(1)△ABC∽△DBA,
△ABC∽△DAC,
△DBA∽△DAC,
3.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出AD2=BD·DC吗?
【选自教材P90 习题4.5 第3题】
3.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出AD2=BD·DC吗?
A
B
C
D
解:(2)能得出AD2=BD·DC.
理由如下:
由(1)可知△DBA∽△DAC,
∴
即
AD2=BD·DC.
【选自教材P90 习题4.5 第3题】
4.将两个全等的等腰直角三角形摆成如图所示的样子,(图中的所有点、线都在同一平面内),请在图中找出两对相似而不全等的三角形,并说明它们相似的理由.
A
B
C
D
E
F
G
解:△ABE∽△DAE.
理由:∠BEA=∠AED,
∠B=∠DAE=45°,
△ADC∽△EDA.
理由:∠CDA=∠ADE,
∠DCA=∠DAE=45°.
【选自教材P90 习题4.5 第4题】
5.如图,为了测量一个大峡谷的宽度,位于峡谷一侧的地质勘探人员在对面的岩石上观察一个特别明显的标志点O,再在他们所在这一侧选点A、B、D,使得AB⊥AO,DB⊥AB,然后确定DO和AB的交点C.测得AC=120m,CB=60m,BD=50m,你能帮助他们算出峡谷的宽AO吗?
解:由AB⊥AO,DB⊥AB,
得∠OAC=∠DBC=90°,
又∠ACO=∠BCD,
所以△ACO∽△BCD.
∴
A
O
C
B
D
【选自教材P91 习题4.5 第5题】
两千六百多年前,埃及有个国王,想知道已经给他盖好了的大金字塔的确实高度,于是,命令祭司们去丈量。可是,没有一个祭司知道该怎样测量,在这个问题面前,祭司们个个束手无策。显然,人是不可能爬到那么高大的塔顶上去的;即使爬上去了,由于塔身是斜的,又怎样来测量呢?一时,金字塔的高度成了一个难题。同时悬赏求解答。
趣味拓展
有一个叫法涅斯的学者,看到国王的诏书后,决心解决这个难题。他想了好几个解题的方案,但都行不通。失败并没有使他灰心。法涅斯索性来到外面,一边踱步,一边思索解决的办法,以致撞到树上。于是,他转了个弯,又走下去。太阳把他的影子投到地上,他走到那里,影子也跟到哪里。这时,他突然看到自己的影子,于是想:是不是可以请太阳来帮忙呢?在古埃及人的眼里,太阳是万能的,太阳能给人温暖,能帮助人们确定方向。法涅斯眼前一亮,他清楚记得,早上和傍晚每个物体都拖着一个长长的影子,而中午每个物体的影子都很短……那么,是不是有一个时刻,物体的影子就等于物体的高度呢?他自言自语起来。
想到这里,法涅斯就找了一根竿子,竖在太阳底下,认真观察、测量起来。经过几天的观察、测量,法涅斯终于证实了自己的想法一有一个时候,物体的影子等于物体的高度。于是,他去测量好金字塔底边的长度,并把数据记下来。然后,他毫不犹豫地揭下了悬挂的诏书。国王得到“有人揭下招字” 的报告后,高兴万分,派人把法涅斯召进王官,盛情款待.一切准备停当后,国王选择了一个风和日丽的日子,举行测塔仪式。测塔这天,国王在祭司们的陪同下,和法涅斯一起来到金字塔旁。看热闹的人黑压压一片,喧哗奢,拥挤著,他们等待著庄严的一刻到来。法涅斯站在测塔指挥台上,俨然像个天使,一动也不动地注视著自己的影子。
看看时间快到了,太阳光给每一个在场的人和巨大的金字塔都投下了黑黑的影子。当法涅斯确定他自己的影子已等于他的身高时,便发出了测塔的命令。这时,助手们立即测出了金字塔的阴影的长。接着,法涅斯十分准确地算出了金字塔的高度,最后,他还把测量金字塔高度的秘密告诉大家。场上,发出一阵热烈的欢呼声。显然,法涅斯利用相似三角形的原理测得了塔高。在法涅斯以前,还没有人知道这个原理呢!法涅斯第一次发现、利用这个原理。在那个时代,这是一个伟大的创举!
在这个基础上,法涅斯进一步研究,得出一个法则:在任意两个对应角相等的三角形中,对应边的比率也相等。从而,找到了在任何季节,在任何时候都能测塔高的方法。
①两角分别相等
③两边成比例且其中一边的对角相等
②两边成比例且夹角相等
④三边成比例
课堂小结
(2) 两个条件
①只有一个角相等
②只有两边成比例
类比
分类
两个三角形
相似至少需要
几个条件呢?
(1) 一个条件
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
