湖南省长沙市岳麓区培圣学校2024-2025学年上学期八年级第一次自能练习数学试题卷(图片版,无答案)
文档属性
| 名称 | 湖南省长沙市岳麓区培圣学校2024-2025学年上学期八年级第一次自能练习数学试题卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 442.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 19:01:51 | ||
图片预览


文档简介
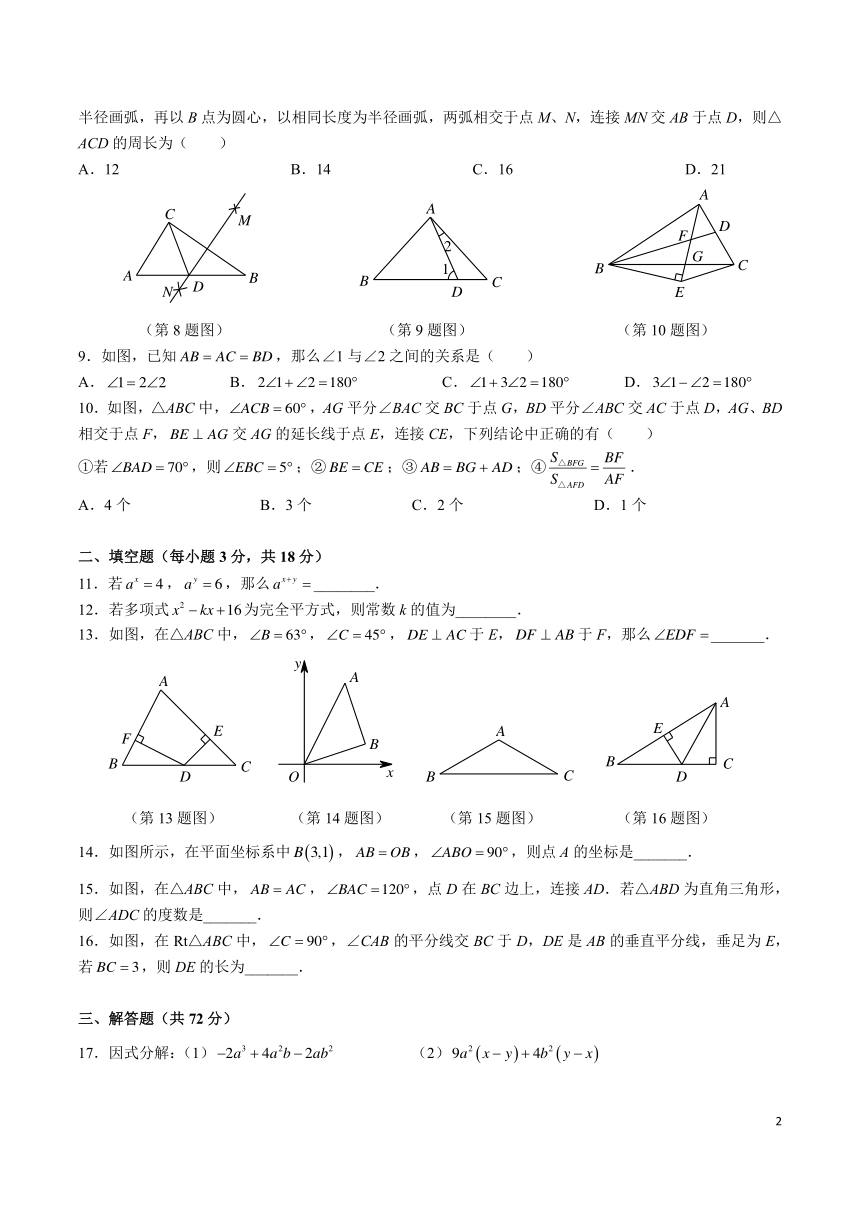
长沙市岳麓区培圣学校 2024-2025 学年度
第一学期八年级第一次自能练习试题卷·数学
总分:120 分 时量:120 分钟
一、选择题(每小题 3分,共计 30分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.以下列各组数据为边长,能构成三角形的是( )
A.4,4,8 B.2,4,7 C.4,8,8 D.2,2,7
3.下列运算正确的是( )
A. (a + b) = a2 + b2 B. 2a3 3a2 = 6a6 C. a4 a3 = a D. a7 a2 = a5
4.将一副三角板按图中方式叠放,则 的度数为( )
A.85° B.95° C.105° D.115°
a b a
C
a-b
α a
A B b
D b
(第 4 题图) (第 5 题图) (第 6 题图)
5.如图,在△ABC中, ACB = 90 ,CD是 AB边上的高, A = 30 ,则下列结论中正确的是( )
A. AC = 2AD B.CD = 2BD C. BC = 2CD D. BC = 2BD
6.观察下图,用等式表示下图中图形面积的运算为( )
2 2 2
A. (a b) = a 2ab + b B. (a + b)(a b) = a2 b2
2
C. a ( ) 2 2a + b = a2 + ab D. (a + b) = a + ab + b
7.如图,△ABC中边 AC上的高是( )
D
A D A AA
C C C C
B D B B B D
A. B. C. D.
1
8.如图,在△ABC中,AC = 5,BC = 7 , AB = 9,用尺规作图的方法:以 C点为圆心,以大于 BC 长为
2
1
{#{QQABJKQQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
半径画弧,再以 B点为圆心,以相同长度为半径画弧,两弧相交于点 M、N,连接 MN交 AB于点 D,则△
ACD的周长为( )
A.12 B.14 C.16 D.21
A
C AM D
F
2
G
A 1
B C
B
N D
B C
D E
(第 8 题图) (第 9 题图) (第 10 题图)
9.如图,已知 AB = AC = BD,那么∠1 与∠2 之间的关系是( )
A. 1= 2 2 B. 2 1+ 2 =180 C. 1+ 3 2 =180 D.3 1 2 =180
10.如图,△ABC中, ACB = 60 ,AG平分∠BAC交 BC于点 G,BD平分∠ABC交 AC于点 D,AG、BD
相交于点 F, BE ⊥ AG 交 AG的延长线于点 E,连接 CE,下列结论中正确的有( )
S△BFG BF①若 BAD = 70 ,则 EBC = 5 ;② BE = CE ;③ AB = BG + AD ;④ = .
S△AFD AF
A.4 个 B.3 个 C.2 个 D.1 个
二、填空题(每小题 3分,共 18分)
11.若 ax = 4, a y = 6,那么 ax+ y = ________.
12.若多项式 x2 kx +16为完全平方式,则常数 k的值为________.
13.如图,在△ABC中, B = 63 , C = 45 ,DE ⊥ AC 于 E,DF ⊥ AB 于 F,那么 EDF = _______.
y
A A
A
E A E
F B
B C B C
D O x B C D
(第 13 题图) (第 14 题图) (第 15 题图) (第 16 题图)
14.如图所示,在平面坐标系中 B(3,1), AB = OB, ABO = 90 ,则点 A的坐标是_______.
15.如图,在△ABC 中, AB = AC , BAC =120 ,点 D在 BC 边上,连接 AD.若△ABD为直角三角形,
则∠ADC的度数是_______.
16.如图,在 Rt△ABC 中, C = 90 ,∠CAB 的平分线交 BC 于 D,DE 是 AB 的垂直平分线,垂足为 E,
若 BC = 3,则 DE的长为_______.
三、解答题(共 72分)
17.因式分解:(1) 2a3 + 4a2b 2ab2 (2)9a2 (x y) + 4b2 ( y x)
2
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
2 1
18.先化简,再求值; (x 2y) (x + y)(3x y) 5y2 (2x),其中 x = 2 , y = .
2
19.已知m + n = 4 ,mn = 2 .
n
(1)当 时,求 am an ma = 2 (a ) 的值;
2
(2)求 (m n) 的值.
20.如图,在平面直角坐标系中,△ABC的三个顶点分别为 A、B、C.
(1)在图中作出△ABC关于 y轴的对称图形△A1B1C1.
(2)求△ABC的面积.
(3)在 x轴上画出点 P,使 PA + PC 最小.
y
A
C
B
O x
3
{#{QQABJKQQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
21.如图,在△ABC中,D为 AB上一点,E为 AC中点,连接 DE并延长至点 F,使得 EF = ED,连 CF.
(1)求证:CF∥AB
(2)若 A = 70 , F = 35 , BE ⊥ AC ,求∠BED的度数.
A
E F
D
B C
22.为迎接培圣校园科技节的到来,学校科技社团欲购买甲、乙两种模型进行组装,已知 3 套甲模型的总价
与 2 套乙模型的总价相等,若购买 1 套甲模型和 2 套乙模型共需 80 元.
(1)求甲、乙两种模型的单价各是多少元?
(2)现计划用 1220 元资金,在不超过预算的情况下,购买这两种模型共 50 套,且乙种模型的数量不少于
2
甲种模型数量的 ,求两种模型共有多少种选购方案.
3
23.如图,等腰△ABC 中, AB = AC , BAC =120 , AD ⊥ BC 于点 D,点 P 是 BA 延长线上一点,点 O
是线段 AD上一点,OP = OC ,连接 OB.
(1)已知: ABO =17 ,求∠DCO的度数;
(2)求证: AB = AO + AP.
P
A
O
B C
D
4
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
24.我们定义:一个整数能表示成 a2 + b2(a、b是整数)的形式,则称这个数为“完美数”.
例如,5 是“完美数”.理由:因为5 = 22 +12 ,所以 5 是“完美数”.
[解决问题]
(1)已知 29 是“完美数”,请将它写成 a2 + b2(a、b 是整数)的形式________;若 x2 6x + 5可配方成
2
(x m) + n (m、n为常数),则mn = ________;
[探究问题]
(2)已知 x2 + y2 2x + 4y + 5 = 0 ,则 ________;已知 S = x2x + y = + 4y2 + 4x 12y + k(x、y是整数,k是
常数),要使 S为“完美数”,试求出符合条件的一个 k值,并说明理由.
[拓展结论]
2 5(3)已知实数 x、y满足 x + x + y 5 = 0 ,求 x 2y 的最值.
2
5
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
25.在直角坐标系中,A点的坐标为 (a,0),B点在 y轴负半轴上,且OA = OB ,E点与 B点关于 x轴对称,
C点的坐标为 (c,0),且 a、b、c满足 a2 6a + 9 + (c2 + 2c +1) = 0.
(1)写出 A、B、C三点的坐标:A______,B______,C______;
(2)如图 1,x轴上一点M位于 A点右侧,连接 BM、EM,延长 BA至 N,使 M位于 BN的垂直平分线上,
且 EM ⊥ MN .若 S△ ,求点 M的坐标; AMN = 2S△AMB
(3)如图 2,点 P为 x轴上 A点右侧的一个动点,Q (1,2),先作直线 PQ,作 AH ⊥ PQ,垂足为 H,在射
线 HQ上取一点 G,满足 HG = HA,连接 CG.请问:在点 P 运动过程中,∠CGQ的大小是否发生变化?
若不变,求出其值;若变化,直接写其变化范围.
y
N
y
E
Q
A G
O M x H
B C O A P x
图 1 图 2
6
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
第一学期八年级第一次自能练习试题卷·数学
总分:120 分 时量:120 分钟
一、选择题(每小题 3分,共计 30分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.以下列各组数据为边长,能构成三角形的是( )
A.4,4,8 B.2,4,7 C.4,8,8 D.2,2,7
3.下列运算正确的是( )
A. (a + b) = a2 + b2 B. 2a3 3a2 = 6a6 C. a4 a3 = a D. a7 a2 = a5
4.将一副三角板按图中方式叠放,则 的度数为( )
A.85° B.95° C.105° D.115°
a b a
C
a-b
α a
A B b
D b
(第 4 题图) (第 5 题图) (第 6 题图)
5.如图,在△ABC中, ACB = 90 ,CD是 AB边上的高, A = 30 ,则下列结论中正确的是( )
A. AC = 2AD B.CD = 2BD C. BC = 2CD D. BC = 2BD
6.观察下图,用等式表示下图中图形面积的运算为( )
2 2 2
A. (a b) = a 2ab + b B. (a + b)(a b) = a2 b2
2
C. a ( ) 2 2a + b = a2 + ab D. (a + b) = a + ab + b
7.如图,△ABC中边 AC上的高是( )
D
A D A AA
C C C C
B D B B B D
A. B. C. D.
1
8.如图,在△ABC中,AC = 5,BC = 7 , AB = 9,用尺规作图的方法:以 C点为圆心,以大于 BC 长为
2
1
{#{QQABJKQQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
半径画弧,再以 B点为圆心,以相同长度为半径画弧,两弧相交于点 M、N,连接 MN交 AB于点 D,则△
ACD的周长为( )
A.12 B.14 C.16 D.21
A
C AM D
F
2
G
A 1
B C
B
N D
B C
D E
(第 8 题图) (第 9 题图) (第 10 题图)
9.如图,已知 AB = AC = BD,那么∠1 与∠2 之间的关系是( )
A. 1= 2 2 B. 2 1+ 2 =180 C. 1+ 3 2 =180 D.3 1 2 =180
10.如图,△ABC中, ACB = 60 ,AG平分∠BAC交 BC于点 G,BD平分∠ABC交 AC于点 D,AG、BD
相交于点 F, BE ⊥ AG 交 AG的延长线于点 E,连接 CE,下列结论中正确的有( )
S△BFG BF①若 BAD = 70 ,则 EBC = 5 ;② BE = CE ;③ AB = BG + AD ;④ = .
S△AFD AF
A.4 个 B.3 个 C.2 个 D.1 个
二、填空题(每小题 3分,共 18分)
11.若 ax = 4, a y = 6,那么 ax+ y = ________.
12.若多项式 x2 kx +16为完全平方式,则常数 k的值为________.
13.如图,在△ABC中, B = 63 , C = 45 ,DE ⊥ AC 于 E,DF ⊥ AB 于 F,那么 EDF = _______.
y
A A
A
E A E
F B
B C B C
D O x B C D
(第 13 题图) (第 14 题图) (第 15 题图) (第 16 题图)
14.如图所示,在平面坐标系中 B(3,1), AB = OB, ABO = 90 ,则点 A的坐标是_______.
15.如图,在△ABC 中, AB = AC , BAC =120 ,点 D在 BC 边上,连接 AD.若△ABD为直角三角形,
则∠ADC的度数是_______.
16.如图,在 Rt△ABC 中, C = 90 ,∠CAB 的平分线交 BC 于 D,DE 是 AB 的垂直平分线,垂足为 E,
若 BC = 3,则 DE的长为_______.
三、解答题(共 72分)
17.因式分解:(1) 2a3 + 4a2b 2ab2 (2)9a2 (x y) + 4b2 ( y x)
2
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
2 1
18.先化简,再求值; (x 2y) (x + y)(3x y) 5y2 (2x),其中 x = 2 , y = .
2
19.已知m + n = 4 ,mn = 2 .
n
(1)当 时,求 am an ma = 2 (a ) 的值;
2
(2)求 (m n) 的值.
20.如图,在平面直角坐标系中,△ABC的三个顶点分别为 A、B、C.
(1)在图中作出△ABC关于 y轴的对称图形△A1B1C1.
(2)求△ABC的面积.
(3)在 x轴上画出点 P,使 PA + PC 最小.
y
A
C
B
O x
3
{#{QQABJKQQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
21.如图,在△ABC中,D为 AB上一点,E为 AC中点,连接 DE并延长至点 F,使得 EF = ED,连 CF.
(1)求证:CF∥AB
(2)若 A = 70 , F = 35 , BE ⊥ AC ,求∠BED的度数.
A
E F
D
B C
22.为迎接培圣校园科技节的到来,学校科技社团欲购买甲、乙两种模型进行组装,已知 3 套甲模型的总价
与 2 套乙模型的总价相等,若购买 1 套甲模型和 2 套乙模型共需 80 元.
(1)求甲、乙两种模型的单价各是多少元?
(2)现计划用 1220 元资金,在不超过预算的情况下,购买这两种模型共 50 套,且乙种模型的数量不少于
2
甲种模型数量的 ,求两种模型共有多少种选购方案.
3
23.如图,等腰△ABC 中, AB = AC , BAC =120 , AD ⊥ BC 于点 D,点 P 是 BA 延长线上一点,点 O
是线段 AD上一点,OP = OC ,连接 OB.
(1)已知: ABO =17 ,求∠DCO的度数;
(2)求证: AB = AO + AP.
P
A
O
B C
D
4
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
24.我们定义:一个整数能表示成 a2 + b2(a、b是整数)的形式,则称这个数为“完美数”.
例如,5 是“完美数”.理由:因为5 = 22 +12 ,所以 5 是“完美数”.
[解决问题]
(1)已知 29 是“完美数”,请将它写成 a2 + b2(a、b 是整数)的形式________;若 x2 6x + 5可配方成
2
(x m) + n (m、n为常数),则mn = ________;
[探究问题]
(2)已知 x2 + y2 2x + 4y + 5 = 0 ,则 ________;已知 S = x2x + y = + 4y2 + 4x 12y + k(x、y是整数,k是
常数),要使 S为“完美数”,试求出符合条件的一个 k值,并说明理由.
[拓展结论]
2 5(3)已知实数 x、y满足 x + x + y 5 = 0 ,求 x 2y 的最值.
2
5
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
25.在直角坐标系中,A点的坐标为 (a,0),B点在 y轴负半轴上,且OA = OB ,E点与 B点关于 x轴对称,
C点的坐标为 (c,0),且 a、b、c满足 a2 6a + 9 + (c2 + 2c +1) = 0.
(1)写出 A、B、C三点的坐标:A______,B______,C______;
(2)如图 1,x轴上一点M位于 A点右侧,连接 BM、EM,延长 BA至 N,使 M位于 BN的垂直平分线上,
且 EM ⊥ MN .若 S△ ,求点 M的坐标; AMN = 2S△AMB
(3)如图 2,点 P为 x轴上 A点右侧的一个动点,Q (1,2),先作直线 PQ,作 AH ⊥ PQ,垂足为 H,在射
线 HQ上取一点 G,满足 HG = HA,连接 CG.请问:在点 P 运动过程中,∠CGQ的大小是否发生变化?
若不变,求出其值;若变化,直接写其变化范围.
y
N
y
E
Q
A G
O M x H
B C O A P x
图 1 图 2
6
{#{QQABKJ QQoExgggAigQAkoBSAACQh5CqUw0XW8YCCQAuGQQkIkIhALEUAgAMYgVOCxNFAOAIZACIAiZiQFFAABBKCAA=}=#}}#}
同课章节目录
