湖南省长沙麓山国际实验学校2024—2025学年上学期第一次月考八年级数学试题(图片版,无答案)
文档属性
| 名称 | 湖南省长沙麓山国际实验学校2024—2025学年上学期第一次月考八年级数学试题(图片版,无答案) |
|
|
| 格式 | |||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 00:00:00 | ||
图片预览



文档简介
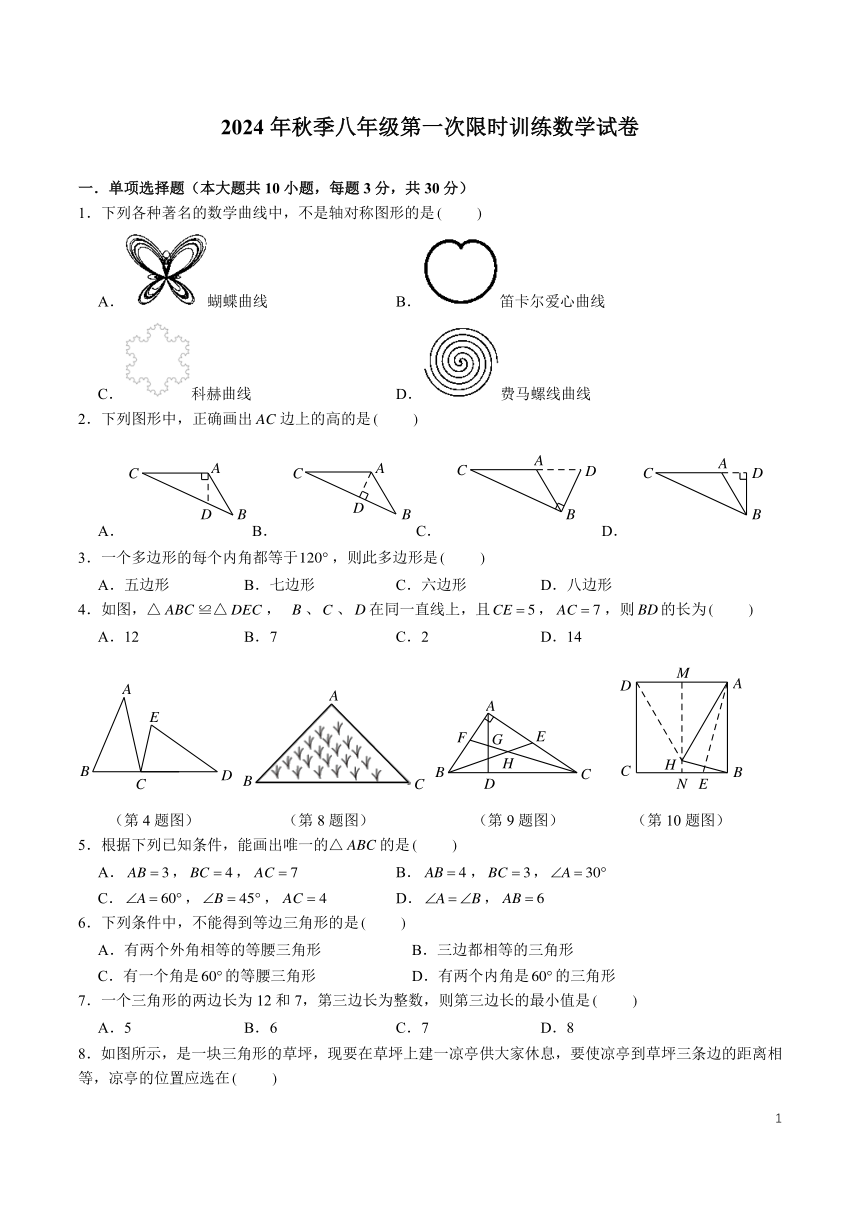
2024 年秋季八年级第一次限时训练数学试卷
一.单项选择题(本大题共 10小题,每题 3分,共 30分)
1.下列各种著名的数学曲线中,不是轴对称图形的是 ( )
A. 蝴蝶曲线 B. 笛卡尔爱心曲线
C. 科赫曲线 D. 费马螺线曲线
2.下列图形中,正确画出 AC 边上的高的是 ( )
A
C A C A C
A
D C D
D B D B B B
A. B. C. D.
3.一个多边形的每个内角都等于120 ,则此多边形是 ( )
A.五边形 B.七边形 C.六边形 D.八边形
4.如图,△ ABC ≌△ DEC , B 、C 、 D 在同一直线上,且CE = 5, AC = 7 ,则 BD的长为 ( )
A.12 B.7 C.2 D.14
M
A D AA
A
E
F G E
H
B C HD B B
C B
C
C D N E
(第 4 题图) (第 8 题图) (第 9 题图) (第 10 题图)
5.根据下列已知条件,能画出唯一的△ ABC 的是 ( )
A. AB = 3, BC = 4, AC = 7 B. AB = 4 , BC = 3, A = 30
C. A = 60 , B = 45 , AC = 4 D. A = B, AB = 6
6.下列条件中,不能得到等边三角形的是 ( )
A.有两个外角相等的等腰三角形 B.三边都相等的三角形
C.有一个角是 60 的等腰三角形 D.有两个内角是60 的三角形
7.一个三角形的两边长为 12 和 7,第三边长为整数,则第三边长的最小值是 ( )
A.5 B.6 C.7 D.8
8.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相
等,凉亭的位置应选在 ( )
1
{#{QQABKJ QQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
A.△ ABC 三条中线的交点 B.△ ABC 三边的垂直平分线的交点
C.△ ABC 三条角平分线的交点 D.△ ABC 三条高所在直线的交点
9.如图,在△ ABC 中, BAC = 90 , AD 是高,BE 是中线,CF 是角平分线,CF 交 AD 于点G ,交 BE
于点H ,下面说法正确的是 ( )
①△ ABE的面积=△ BCE 的面积;② AFG = AGF ;③ FAG = 2 ACF ;④ AF = FB .
A.①②③④ B.①②④ C.①②③ D.③④
10.如图,先将正方形纸片对折,折痕为MN ,再把 B 点折叠在折痕MN 上,折痕为 AE ,点 B 在MN 上的
对应点为H ,沿 AH 和 DH 剪下得到△ ADH ,则下列选项正确的个数为 ( )
① AE 垂直平分 HB;② HBN =15 ;③ DH = DC ;④△ ADH 是一个等边三角形.
A.1 个 B.2 个 C.3 个 D.4 个
二.填空题(本大题共 6小题,每题 3分,共 18分)
11.点 P(1, 2)关于 y 轴对称的点的坐标为 .
12.在Rt △ ABC 中, C = 90 , A = 30 , AB = 6cm ,则 BC = cm .
13.如图, ACD 是△ ABC 的外角,若 A = 35 , B = 40 ,则 1的度数为 .
l
C 1
A A l2
D
B
1 C
B D A B
C E O
(第 13 题图) (第 14 题图) (第 15 题图)
14.如图三角形纸片中,AB = 8cm,BC = 6cm,AC = 5cm,沿过点 B 的直线折叠这个三角形,使点C 落在
AB 边上的点 E 处,折痕为 BD,则△ AED的周长为 cm .
15.如图,△ ABC 的边 BC , AC 的垂直平分线 l , l 相交于点O .若 A =110 ,则 BOC =1 2 .
16.若等腹三角形的两条高所在直线形成的角中有一个为 45 , 则其顶角的度数为 .
三.解答题(本大题共 9小题,共 72分)
17.(6 分)计算: 12024+ | 5 2 | ( 3)0 + ( 2)2
2
{#{QQABKJ QQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
18.(6 分)如图,网格中的△ ABC 和△ DEF 是轴对称图形.
(1)利用网格线,作出△ ABC 和△ DEF 的对称轴 l ;
(2)如果每个小正方形的边长为 1,求△ ABC 的面积.
A
B
C
D
F
E
19.(8 分)已知:如图,点 E , F 在 BC 上, BE = CF , AB = DC , B = C .求证: A = D.
A D
B C
E F
20.(8 分)用一条长为 20cm 的细绳围成一个等腰三角形.
(1)若腰长比底边长短 2cm,求它的三边长;
(2)能围成有一边的长是 4cm的等腰三角形吗?若能,请求出它的另两边;若不能,请说明理由.
3
{#{QQABKJ QQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
21.(8 分)如图, AB = AC , AD = BC , AB 的垂直平分线MN 交 AC 于点D ,求 DBC 的度数.
A
M
D
N
B C
22.(8 分)如图,过等边△ ABC 的顶点 A,B ,C 依次作 AB ,BC ,CA 的垂线MG ,MN ,NG ,三条
垂线围成△MNG ,求证:△MNG 是等边三角形.
M
A
G
B C
N
23.(8 分)(1)如图 1,在△ ABC 中, AB = AC , BAC = 90 ,CD平分 ACB ,BE ⊥ CD ,垂足为 E ,
试探究线段 BE 和CD之间的数量关系,并写出你的理由.
1
(2)如图 2,把条件改为:“在△ ABC 中,AB = AC , BAC = 90 ,点D 在 BC 上, EDB = C ,BE ⊥ ED ,
2
DE 与 AB 相交于 F 点,则线段 BE 和 FD之间的数量关系如何?并证明你的结论.”
A
A
E
E
D F
B C
B C D
4
{#{QQABJKQQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
24.(10 分)如图,点 A(a,0) , B(0,b) ,满足 (a 1)2+ | 2 2b |= 0,若点 P 为射线OA上异于原点O 和点 A
的一个动点.
y y y
B B B
E
O P A x O A x O A x
图 1 备用图 备用图
(1)如图 1,
①直接写出点 A的坐标为 ,点 B 的坐标为 ;
②当点 P 位于点O 与点 A之间时,连接 PB,以线段 PB为边作等腰直角△ BPE( P 为直角顶点,B ,P ,
E 按逆时针方向排列),连接 AE .求证: AB ⊥ AE ;
(2)点 D 是直线 AB 上异于点 A与点 B 的一点,使得 BPO = APD,过点 D 作 DF ⊥ BP交 y 轴于点 F ,
探究 BP, DP, DF 之间的数量关系,并证明.
5
{#{QQABJKQQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
25.(10 分)(1)如图 1,学习了等腰三角形,我们知道:在一个三角形中,等边所对的角相等;反过来,
等角所对的边也相等.如果在一个三角形中,两个角不等,那么它们所对的边有什么大小关系呢?猜想:在
△ ABC 中,如果 AB AC ,则 C B(填写“ ”“ ”或“=” ),请证明你的猜想;
(2)如图 2,在△ ABC 中( AB BC ), BP平分 ABC 交 AC 于点D ,连接 AP ,CP .判断 AB BC 与
PC PA的大小关系,并证明;
DE 5 BD
(3)如图 3,在△ ABC 中, A = 60 ,△ ABC 的角平分线 BF ,CE 交于点D ,若 = ,求 的值.
CD 7 CD
A
A
A
E
P FD D
B C B C B C
图 1 图 2 图 3
6
{#{QQABJKQQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
一.单项选择题(本大题共 10小题,每题 3分,共 30分)
1.下列各种著名的数学曲线中,不是轴对称图形的是 ( )
A. 蝴蝶曲线 B. 笛卡尔爱心曲线
C. 科赫曲线 D. 费马螺线曲线
2.下列图形中,正确画出 AC 边上的高的是 ( )
A
C A C A C
A
D C D
D B D B B B
A. B. C. D.
3.一个多边形的每个内角都等于120 ,则此多边形是 ( )
A.五边形 B.七边形 C.六边形 D.八边形
4.如图,△ ABC ≌△ DEC , B 、C 、 D 在同一直线上,且CE = 5, AC = 7 ,则 BD的长为 ( )
A.12 B.7 C.2 D.14
M
A D AA
A
E
F G E
H
B C HD B B
C B
C
C D N E
(第 4 题图) (第 8 题图) (第 9 题图) (第 10 题图)
5.根据下列已知条件,能画出唯一的△ ABC 的是 ( )
A. AB = 3, BC = 4, AC = 7 B. AB = 4 , BC = 3, A = 30
C. A = 60 , B = 45 , AC = 4 D. A = B, AB = 6
6.下列条件中,不能得到等边三角形的是 ( )
A.有两个外角相等的等腰三角形 B.三边都相等的三角形
C.有一个角是 60 的等腰三角形 D.有两个内角是60 的三角形
7.一个三角形的两边长为 12 和 7,第三边长为整数,则第三边长的最小值是 ( )
A.5 B.6 C.7 D.8
8.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相
等,凉亭的位置应选在 ( )
1
{#{QQABKJ QQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
A.△ ABC 三条中线的交点 B.△ ABC 三边的垂直平分线的交点
C.△ ABC 三条角平分线的交点 D.△ ABC 三条高所在直线的交点
9.如图,在△ ABC 中, BAC = 90 , AD 是高,BE 是中线,CF 是角平分线,CF 交 AD 于点G ,交 BE
于点H ,下面说法正确的是 ( )
①△ ABE的面积=△ BCE 的面积;② AFG = AGF ;③ FAG = 2 ACF ;④ AF = FB .
A.①②③④ B.①②④ C.①②③ D.③④
10.如图,先将正方形纸片对折,折痕为MN ,再把 B 点折叠在折痕MN 上,折痕为 AE ,点 B 在MN 上的
对应点为H ,沿 AH 和 DH 剪下得到△ ADH ,则下列选项正确的个数为 ( )
① AE 垂直平分 HB;② HBN =15 ;③ DH = DC ;④△ ADH 是一个等边三角形.
A.1 个 B.2 个 C.3 个 D.4 个
二.填空题(本大题共 6小题,每题 3分,共 18分)
11.点 P(1, 2)关于 y 轴对称的点的坐标为 .
12.在Rt △ ABC 中, C = 90 , A = 30 , AB = 6cm ,则 BC = cm .
13.如图, ACD 是△ ABC 的外角,若 A = 35 , B = 40 ,则 1的度数为 .
l
C 1
A A l2
D
B
1 C
B D A B
C E O
(第 13 题图) (第 14 题图) (第 15 题图)
14.如图三角形纸片中,AB = 8cm,BC = 6cm,AC = 5cm,沿过点 B 的直线折叠这个三角形,使点C 落在
AB 边上的点 E 处,折痕为 BD,则△ AED的周长为 cm .
15.如图,△ ABC 的边 BC , AC 的垂直平分线 l , l 相交于点O .若 A =110 ,则 BOC =1 2 .
16.若等腹三角形的两条高所在直线形成的角中有一个为 45 , 则其顶角的度数为 .
三.解答题(本大题共 9小题,共 72分)
17.(6 分)计算: 12024+ | 5 2 | ( 3)0 + ( 2)2
2
{#{QQABKJ QQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
18.(6 分)如图,网格中的△ ABC 和△ DEF 是轴对称图形.
(1)利用网格线,作出△ ABC 和△ DEF 的对称轴 l ;
(2)如果每个小正方形的边长为 1,求△ ABC 的面积.
A
B
C
D
F
E
19.(8 分)已知:如图,点 E , F 在 BC 上, BE = CF , AB = DC , B = C .求证: A = D.
A D
B C
E F
20.(8 分)用一条长为 20cm 的细绳围成一个等腰三角形.
(1)若腰长比底边长短 2cm,求它的三边长;
(2)能围成有一边的长是 4cm的等腰三角形吗?若能,请求出它的另两边;若不能,请说明理由.
3
{#{QQABKJ QQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
21.(8 分)如图, AB = AC , AD = BC , AB 的垂直平分线MN 交 AC 于点D ,求 DBC 的度数.
A
M
D
N
B C
22.(8 分)如图,过等边△ ABC 的顶点 A,B ,C 依次作 AB ,BC ,CA 的垂线MG ,MN ,NG ,三条
垂线围成△MNG ,求证:△MNG 是等边三角形.
M
A
G
B C
N
23.(8 分)(1)如图 1,在△ ABC 中, AB = AC , BAC = 90 ,CD平分 ACB ,BE ⊥ CD ,垂足为 E ,
试探究线段 BE 和CD之间的数量关系,并写出你的理由.
1
(2)如图 2,把条件改为:“在△ ABC 中,AB = AC , BAC = 90 ,点D 在 BC 上, EDB = C ,BE ⊥ ED ,
2
DE 与 AB 相交于 F 点,则线段 BE 和 FD之间的数量关系如何?并证明你的结论.”
A
A
E
E
D F
B C
B C D
4
{#{QQABJKQQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
24.(10 分)如图,点 A(a,0) , B(0,b) ,满足 (a 1)2+ | 2 2b |= 0,若点 P 为射线OA上异于原点O 和点 A
的一个动点.
y y y
B B B
E
O P A x O A x O A x
图 1 备用图 备用图
(1)如图 1,
①直接写出点 A的坐标为 ,点 B 的坐标为 ;
②当点 P 位于点O 与点 A之间时,连接 PB,以线段 PB为边作等腰直角△ BPE( P 为直角顶点,B ,P ,
E 按逆时针方向排列),连接 AE .求证: AB ⊥ AE ;
(2)点 D 是直线 AB 上异于点 A与点 B 的一点,使得 BPO = APD,过点 D 作 DF ⊥ BP交 y 轴于点 F ,
探究 BP, DP, DF 之间的数量关系,并证明.
5
{#{QQABJKQQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
25.(10 分)(1)如图 1,学习了等腰三角形,我们知道:在一个三角形中,等边所对的角相等;反过来,
等角所对的边也相等.如果在一个三角形中,两个角不等,那么它们所对的边有什么大小关系呢?猜想:在
△ ABC 中,如果 AB AC ,则 C B(填写“ ”“ ”或“=” ),请证明你的猜想;
(2)如图 2,在△ ABC 中( AB BC ), BP平分 ABC 交 AC 于点D ,连接 AP ,CP .判断 AB BC 与
PC PA的大小关系,并证明;
DE 5 BD
(3)如图 3,在△ ABC 中, A = 60 ,△ ABC 的角平分线 BF ,CE 交于点D ,若 = ,求 的值.
CD 7 CD
A
A
A
E
P FD D
B C B C B C
图 1 图 2 图 3
6
{#{QQABJKQQsA5oggi4AkIIAbIAIACAAA5hqCUU0wHGcC4QCuAQGkQIMkAhAJUAgCMYBgOVCQJFOAAEZIACIAiJiFAAFBAKBAC=A}=#}#}
同课章节目录
