湖南省长沙市中雅中学2024-2025学年八年级上学期第一次月考数学试卷(图片版,无答案)
文档属性
| 名称 | 湖南省长沙市中雅中学2024-2025学年八年级上学期第一次月考数学试卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 407.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 19:05:39 | ||
图片预览


文档简介
2024 年下学期八年级 10 月随堂练习
数学科目
“考生注意:本试卷共三道大题,25 道小题,满分 120 分,时量 120 分钟”
一、选择题(每小题 3 分,共 30 分)
1.下图中为轴对称图形的是( )
A.中 B.雅 C.培 D.粹
2.下列各组线段中能围成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.14cm,12cm,20cm D.5cm,5cm,11cm
3.已知图中的两个三角形全等,则∠α等于( )
A.72° B.60° C.58° D.50°
A D C
50°
a c a E H
58° 72° α B C B A
b c E F F D
(第 3 题图) (第 4 题图) (第 10 题图)
4.如图,点 E,F在 BC上,BF = CE , A = D.要使△ABF≌△DCE,需要添加下列选项中的( )
A. AF = DE B. AB = CD C. BE = CF D. B = C
5.等腰三角形的一个角是 100°,它的底角的大小为( )
A.40° B.100° C.80° D.40°或 100°
6.下列图形中不具有稳定性的是( )
A. B. C. D.
7.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A. A = 30 , B = 60 C. A = 40 , B = 70
B. A = 70 , B = 50 D. A = 60 , B = 80
8.下列说法正确的是( )
A.如果两个三角形全等,则它们必关于某条直线成轴对称.
1
{#{QQABILQQ66Eoo5giAwAIkIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形.
C.等腰三角形的对称轴是一条边上的中线所在的直线.
D.所有的轴对称图形都只有一条对称轴.
9.一个多边形的内角和是外角和的四倍,它是几边形?( )
A.四 B.六 C.八 D.十
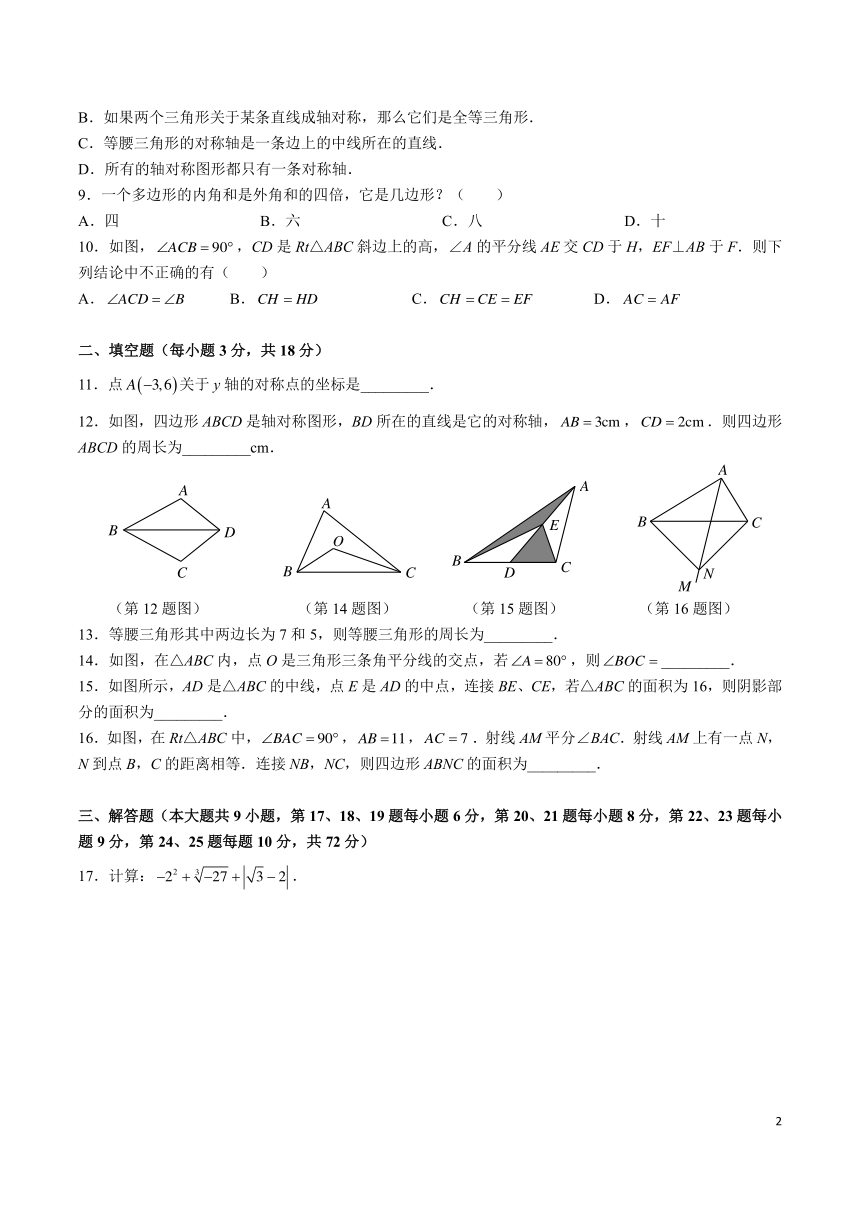
10.如图, ACB = 90 ,CD是 Rt△ABC斜边上的高,∠A的平分线 AE交 CD于 H,EF⊥AB于 F.则下
列结论中不正确的有( )
A. ACD = B B.CH = HD C.CH = CE = EF D. AC = AF
二、填空题(每小题 3 分,共 18 分)
11.点 A( 3,6)关于 y轴的对称点的坐标是_________.
12.如图,四边形 ABCD是轴对称图形,BD所在的直线是它的对称轴, AB = 3cm ,CD = 2cm.则四边形
ABCD的周长为_________cm.
A
A A
A
B C
B ED
O
B
C B C D C N
M
(第 12 题图) (第 14 题图) (第 15 题图) (第 16 题图)
13.等腰三角形其中两边长为 7 和 5,则等腰三角形的周长为_________.
14.如图,在△ABC内,点 O是三角形三条角平分线的交点,若 A = 80 ,则 BOC = _________.
15.如图所示,AD是△ABC的中线,点 E是 AD的中点,连接 BE、CE,若△ABC的面积为 16,则阴影部
分的面积为_________.
16.如图,在 Rt△ABC中, BAC = 90 ,AB =11,AC = 7 .射线 AM平分∠BAC.射线 AM上有一点 N,
N到点 B,C的距离相等.连接 NB,NC,则四边形 ABNC的面积为_________.
三、解答题(本大题共 9 小题,第 17、18、19 题每小题 6 分,第 20、21 题每小题 8 分,第 22、23 题每小
题 9 分,第 24、25 题每题 10 分,共 72 分)
17.计算: 22 + 3 27 + 3 2 .
2
{#{QQABILQQ66Eoo5giAwAkIIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
5x 7y = 1
18.解方程组:
x + 3y =13
19.老师布置了如下尺规作图的作业:
A
已知:如图△ABC. A
求作:△ABC边 BC上的高 AM.
下面是小红设计的尺规作图过程: B C B
C M D
作法:①延长线段 BC;
②以点 A为圆心,AC长为半径作弧交 BC的延长线于点 D; E
1
③分别以点 C,D为圆心,大于 CD 的长为半径作弧,两弧在 CD下方交于点 E;
2
④连接 AE,交 CD于点M.
如图所示,所以线段 AM就是所求作的高线.
根据小红设计的尺规作图过程和图形,完成问题:
由②可得: AC = _________.
由③可得:_______= _______.
∴_______________(____________________________________________).(填推理的依据)
即 AM是△ABC边 BC上的________线.
20.如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若点 A、B、C的坐标分
别是 A( 2,3), B ( 3,5),C ( 5,2).
(1)画出△ABC关于 x轴对称的图形△A1B1C1 并写出 A1的坐标.
(2)求△ABC的面积.
y
B
A
C
O
x
3
{#{QQABILQQ66Eoo5giAwAIkIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
21.如图, A = D, B = E , AF = CD .
(1)求证: AB = DE .
(2)若 A = 34 , EFD =105 ,求∠B的度数.
B A
C
F
D E
22.如图,点 B,C,D在同一条直线上,BC = DE ,点 A和点 E在 BD的同侧, ACE = B = D = 60 .
(1)求证:△ABC≌△CDE;
(2)若 DE = 3, AB = 4 ,求 BD的长.
A
E
B D
C
23.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.连接 AC,BD交于点 M,连
接 PD.
(1)证明:△AED≌△AFD;
(2)证明:AD垂直平分 EF;
(3)若 DE = 6, S△ = 60,求 AB + ACABC 的长.
A
E
F
B C
D
4
{#{QQABILQQ66Eoo5giAwAIkIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
24.(1)如图 1,OP平分∠MON.点 A为 OM上一点,过点 A作 AC⊥OP,垂足为 C,延长 AC交 ON于
点 B,可根据________证明△AOC≌△BOC.
(2)如图 2,在△ABC中,CD平分∠ACB,AE⊥CD于 E,若 EAC = 65 , B = 38 ,通过(1)中构造
全等的办法,可求得 DAE = _________.
(3)①如图 3,△ABC 中, AB = AC , BAC = 90 ,CD 平分∠ACB,BE⊥CD,垂足 E 在 CD 的延长线
上,只探究 BE和 CD的数量关系,并证明你的结论.
1
②如图 4,△ABC中, AB = AC , BAC = 90 ,点 F在线段 BC上, EFB = C ,BE⊥EF,垂足为 E,
2
EF与 AB相交于点 D.若△BDF的面积为 64,求 BE的长.
N
B AA A
P E
D E
C D
E D
M O B C
A B C B C F
图 1 图 2 图 3 图 4
5
{#{QQABILQQ66Eoo5giAwAkIIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
25.在平面直角坐标系中,A点坐标为 (4,3).
(1)请写出点 A关于 x轴的对称点的坐标为_________;
(2)如图 1,若OA = OB , AOB = 90 ,请求出 B点坐标;
(3)如图 2,在(2)的条件下,若 C 点和 D 点同时从原点出发,以相同的速度分别沿 x 轴和 y 轴的负半
轴方向运动.E点和 F点分别是 CD,AD的中点,连接 EF,BD.请探究 EF与 BD的位置及数量关系,并
说明理由.
y
B
A
y
C
B O x
A F
E
O x D
图 1 图 2
6
{#{QQABLIQQ66Eoo5giAwAkIIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
数学科目
“考生注意:本试卷共三道大题,25 道小题,满分 120 分,时量 120 分钟”
一、选择题(每小题 3 分,共 30 分)
1.下图中为轴对称图形的是( )
A.中 B.雅 C.培 D.粹
2.下列各组线段中能围成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.14cm,12cm,20cm D.5cm,5cm,11cm
3.已知图中的两个三角形全等,则∠α等于( )
A.72° B.60° C.58° D.50°
A D C
50°
a c a E H
58° 72° α B C B A
b c E F F D
(第 3 题图) (第 4 题图) (第 10 题图)
4.如图,点 E,F在 BC上,BF = CE , A = D.要使△ABF≌△DCE,需要添加下列选项中的( )
A. AF = DE B. AB = CD C. BE = CF D. B = C
5.等腰三角形的一个角是 100°,它的底角的大小为( )
A.40° B.100° C.80° D.40°或 100°
6.下列图形中不具有稳定性的是( )
A. B. C. D.
7.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A. A = 30 , B = 60 C. A = 40 , B = 70
B. A = 70 , B = 50 D. A = 60 , B = 80
8.下列说法正确的是( )
A.如果两个三角形全等,则它们必关于某条直线成轴对称.
1
{#{QQABILQQ66Eoo5giAwAIkIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形.
C.等腰三角形的对称轴是一条边上的中线所在的直线.
D.所有的轴对称图形都只有一条对称轴.
9.一个多边形的内角和是外角和的四倍,它是几边形?( )
A.四 B.六 C.八 D.十
10.如图, ACB = 90 ,CD是 Rt△ABC斜边上的高,∠A的平分线 AE交 CD于 H,EF⊥AB于 F.则下
列结论中不正确的有( )
A. ACD = B B.CH = HD C.CH = CE = EF D. AC = AF
二、填空题(每小题 3 分,共 18 分)
11.点 A( 3,6)关于 y轴的对称点的坐标是_________.
12.如图,四边形 ABCD是轴对称图形,BD所在的直线是它的对称轴, AB = 3cm ,CD = 2cm.则四边形
ABCD的周长为_________cm.
A
A A
A
B C
B ED
O
B
C B C D C N
M
(第 12 题图) (第 14 题图) (第 15 题图) (第 16 题图)
13.等腰三角形其中两边长为 7 和 5,则等腰三角形的周长为_________.
14.如图,在△ABC内,点 O是三角形三条角平分线的交点,若 A = 80 ,则 BOC = _________.
15.如图所示,AD是△ABC的中线,点 E是 AD的中点,连接 BE、CE,若△ABC的面积为 16,则阴影部
分的面积为_________.
16.如图,在 Rt△ABC中, BAC = 90 ,AB =11,AC = 7 .射线 AM平分∠BAC.射线 AM上有一点 N,
N到点 B,C的距离相等.连接 NB,NC,则四边形 ABNC的面积为_________.
三、解答题(本大题共 9 小题,第 17、18、19 题每小题 6 分,第 20、21 题每小题 8 分,第 22、23 题每小
题 9 分,第 24、25 题每题 10 分,共 72 分)
17.计算: 22 + 3 27 + 3 2 .
2
{#{QQABILQQ66Eoo5giAwAkIIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
5x 7y = 1
18.解方程组:
x + 3y =13
19.老师布置了如下尺规作图的作业:
A
已知:如图△ABC. A
求作:△ABC边 BC上的高 AM.
下面是小红设计的尺规作图过程: B C B
C M D
作法:①延长线段 BC;
②以点 A为圆心,AC长为半径作弧交 BC的延长线于点 D; E
1
③分别以点 C,D为圆心,大于 CD 的长为半径作弧,两弧在 CD下方交于点 E;
2
④连接 AE,交 CD于点M.
如图所示,所以线段 AM就是所求作的高线.
根据小红设计的尺规作图过程和图形,完成问题:
由②可得: AC = _________.
由③可得:_______= _______.
∴_______________(____________________________________________).(填推理的依据)
即 AM是△ABC边 BC上的________线.
20.如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若点 A、B、C的坐标分
别是 A( 2,3), B ( 3,5),C ( 5,2).
(1)画出△ABC关于 x轴对称的图形△A1B1C1 并写出 A1的坐标.
(2)求△ABC的面积.
y
B
A
C
O
x
3
{#{QQABILQQ66Eoo5giAwAIkIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
21.如图, A = D, B = E , AF = CD .
(1)求证: AB = DE .
(2)若 A = 34 , EFD =105 ,求∠B的度数.
B A
C
F
D E
22.如图,点 B,C,D在同一条直线上,BC = DE ,点 A和点 E在 BD的同侧, ACE = B = D = 60 .
(1)求证:△ABC≌△CDE;
(2)若 DE = 3, AB = 4 ,求 BD的长.
A
E
B D
C
23.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.连接 AC,BD交于点 M,连
接 PD.
(1)证明:△AED≌△AFD;
(2)证明:AD垂直平分 EF;
(3)若 DE = 6, S△ = 60,求 AB + ACABC 的长.
A
E
F
B C
D
4
{#{QQABILQQ66Eoo5giAwAIkIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
24.(1)如图 1,OP平分∠MON.点 A为 OM上一点,过点 A作 AC⊥OP,垂足为 C,延长 AC交 ON于
点 B,可根据________证明△AOC≌△BOC.
(2)如图 2,在△ABC中,CD平分∠ACB,AE⊥CD于 E,若 EAC = 65 , B = 38 ,通过(1)中构造
全等的办法,可求得 DAE = _________.
(3)①如图 3,△ABC 中, AB = AC , BAC = 90 ,CD 平分∠ACB,BE⊥CD,垂足 E 在 CD 的延长线
上,只探究 BE和 CD的数量关系,并证明你的结论.
1
②如图 4,△ABC中, AB = AC , BAC = 90 ,点 F在线段 BC上, EFB = C ,BE⊥EF,垂足为 E,
2
EF与 AB相交于点 D.若△BDF的面积为 64,求 BE的长.
N
B AA A
P E
D E
C D
E D
M O B C
A B C B C F
图 1 图 2 图 3 图 4
5
{#{QQABILQQ66Eoo5giAwAkIIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
25.在平面直角坐标系中,A点坐标为 (4,3).
(1)请写出点 A关于 x轴的对称点的坐标为_________;
(2)如图 1,若OA = OB , AOB = 90 ,请求出 B点坐标;
(3)如图 2,在(2)的条件下,若 C 点和 D 点同时从原点出发,以相同的速度分别沿 x 轴和 y 轴的负半
轴方向运动.E点和 F点分别是 CD,AD的中点,连接 EF,BD.请探究 EF与 BD的位置及数量关系,并
说明理由.
y
B
A
y
C
B O x
A F
E
O x D
图 1 图 2
6
{#{QQABLIQQ66Eoo5giAwAkIIIAbAAChAC5QqQw0GHoMCgCOwQmkQAkGIKAhALYUggOMQBFVACMBMKAZIACiQiZFFABCKA=}}#}}
同课章节目录
