江苏省无锡市锡山高级中学实验学校2024-2025学年八年级数学上学期10月月考卷(图片版,无答案)
文档属性
| 名称 | 江苏省无锡市锡山高级中学实验学校2024-2025学年八年级数学上学期10月月考卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 424.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 19:35:27 | ||
图片预览

文档简介
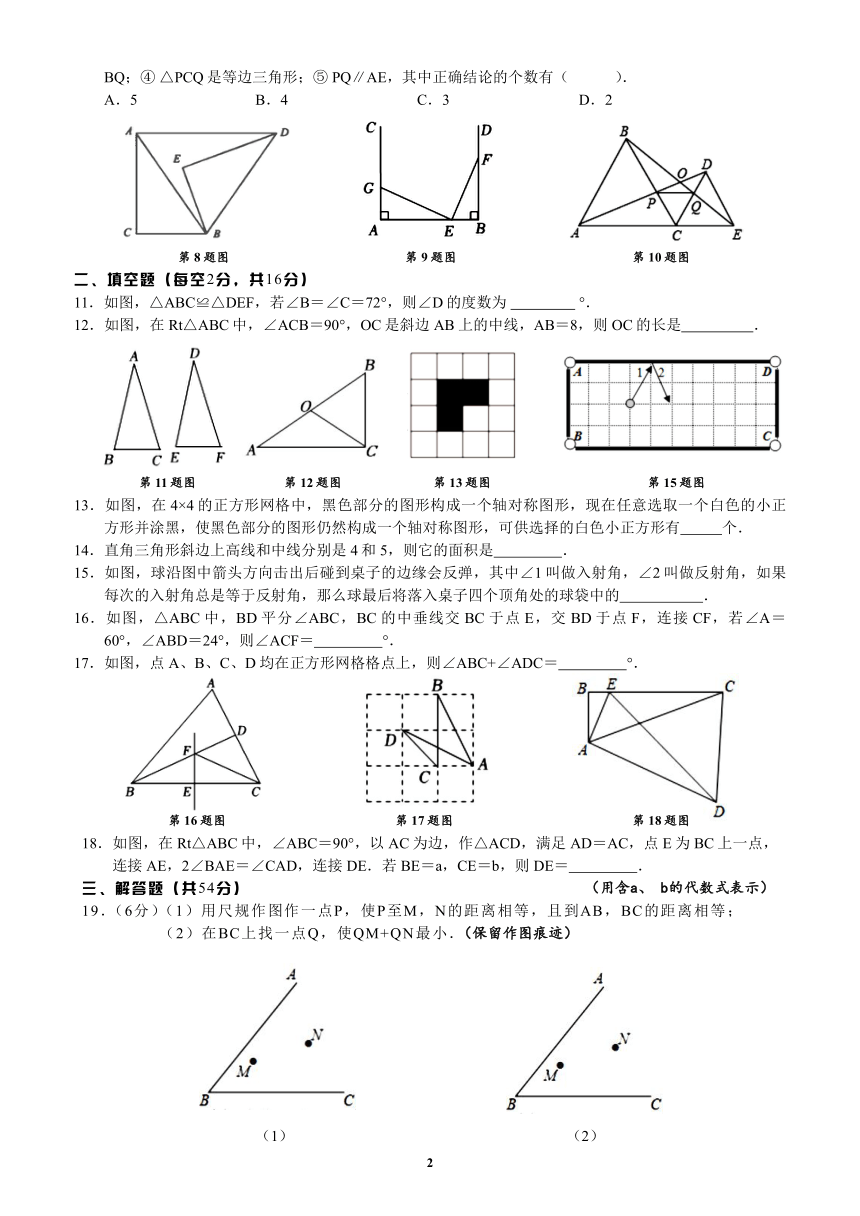
江苏省无锡市锡山高级中学实验学校10月限时作业练习
一、单选题(每题3分,共30分)
1.下列说法错误的是( ).
A.关于某条直线对称的两个三角形一定全等 B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称 D.角是关于它的平分线所在直线对称的图形
2.满足下列条件的三角形,不一定是等边三角形的是( ).
A.有两个内角是 60°的三角形 B.有两边相等且是轴对称图形的三角形
C.有一个内角是 60°且是轴对称图形的三角形 D.三边都相等的三角形
3.在联合会上,有 A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在
他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC
的( ).
A.三边中线的交点 B.三条角平分线交点 C.三边中垂线的交点 D.三边上高交点
4.已知△ABC,下列尺规作图的方法中,能确定∠BAD=∠CAD的是( ).
A. B. C. D.
5.如图,在△ABC中,∠C=90°,若 BC=10,AD平分∠BAC交 BC于点 D;且 BD∶CD=3∶2,则点
D到线段 AB的距离 DE为( ).
A.2 B.4 C.5 D.6
6.如图,直线 m∥n,Rt△ABC的顶点 A在直线 n上,∠C=90°,AB,CB分别交直线 m于点 D和点 E,
且 DB=DE,若∠B=25°,则∠1的度数为( ).
A.60° B.65° C.70° D.75°
第 5题图 第 6题图 第 7题图
7.如图,在△ABC中,∠A=90°,AB=6,AC=8,BC=10,CD平分∠BCA交 AB于点 D,点 P,Q
分别是 CD,AC上的动点,连接 AP,PQ,则 AP+PQ的最小值是( ).
A.6 B.5 C.4.8 D.4
8.如图,△ACB≌△DEB,点 A和点 D是对应顶点,∠C=∠E=90°,记∠CBE=α,∠CAB=β,当
AD∥BC时,α与β之间的数量关系为( ).
A.α=2β B.α=β C.a+β=90° D.α+β=180°
9.如图,∠A=∠B=90°,AB=60,E、F分别为线段 AB和射线 BD上的一点,若点 E从点 B出发向
点 A运动,同时点 F从点 B出发向点 D运动,二者速度之比为 3∶7,运动到某时刻同时停止,在射
线 AC上取一点 G,使△AEG与△BEF全等,则 AG的长为( ).
A.18 B.88 C.88或 62 D.18或 70
10.如图,已知△ABC和△CDE都是等边三角形,且 A、C、E三点共线 AD与 BE交于点 O, AD与 BC
交于点 P,BE 与 CD交于点 Q,连接 PQ.以下五个结论:① AD=BE:② ∠ADB=60°;③ AP=
1
{#{QQABDQywEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
BQ;④ △PCQ是等边三角形;⑤ PQ∥AE,其中正确结论的个数有( ).
A.5 B.4 C.3 D.2
第 8题图 第 9题图 第 10题图
二、填空题(每空2分,共16分)
11.如图,△ABC≌△DEF,若∠B=∠C=72°,则∠D的度数为 °.
12.如图,在 Rt△ABC中,∠ACB=90°,OC是斜边 AB上的中线,AB=8,则 OC的长是 .
第 11题图 第 12题图 第 13题图 第 15题图
13.如图,在 4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正
方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形,可供选择的白色小正方形有 个.
14.直角三角形斜边上高线和中线分别是 4和 5,则它的面积是 .
15.如图,球沿图中箭头方向击出后碰到桌子的边缘会反弹,其中∠1叫做入射角,∠2叫做反射角,如果
每次的入射角总是等于反射角,那么球最后将落入桌子四个顶角处的球袋中的 .
16.如图,△ABC中,BD平分∠ABC,BC 的中垂线交 BC 于点 E,交 BD于点 F,连接 CF,若∠A=
60°,∠ABD=24°,则∠ACF= °.
17.如图,点 A、B、C、D均在正方形网格格点上,则∠ABC+∠ADC= °.
第 16题图 第 17题图 第 18题图
18.如图,在 Rt△ABC中,∠ABC=90°,以 AC为边,作△ACD,满足 AD=AC,点 E为 BC上一点,
连接 AE,2∠BAE=∠CAD,连接 DE.若 BE=a,CE=b,则 DE= .
三、解答题(共54分) (用含a、 b的代数式表示)
19.(6分)(1)用尺规作图作一点P,使P至M,N的距离相等,且到AB,BC的距离相等;
(2)在BC上找一点Q,使QM+QN最小.(保留作图痕迹)
(1) (2)
2
{#{QQABDQywEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
20.(4分)如图,点B、F、C、E四点在同条直线上,∠B=∠E,AB=DE,BF=CE.
求证:∠A=∠D.
21.(6分)如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作BC的平行线与AB,
AC分别相交于点M、N.求证:MN=BM+CN.
22.(6分)已知,如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点.
求证:(1)BM=DM;(2)MN⊥BD.
23.(6分)如图所示,∠A=∠B=90°,P是AB的中点,且DP平分∠ADC,连接PC.
(1)试说明CP平分∠BCD;
(2)线段PD与PC有怎样的位置关系?请说明理由.
24.(8分)如图,已知△ABC,AB=AC,∠B=50°,点D在线段BC上,点E在线段AC上,
设∠BAD=α,∠CDE=β.
(1)如果a=20°,β=10°,那么△ADE是等边三角形?请说明理由;
(2)若AD=AE,试求α与β之间的关系.
3
{#{QQABDQywEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
25.(8分)
(1) [问题发现]
① 如图1,△ABC中,AB=AC,D为BC边上的中点,连接AD.设△ABD的面积和
周长分别为S1和C1,△ACD的面积和周长分别为S2和C2,则S1 S2,C1 C2.
(填“>”,“<”或“=”)
1
② 如图2,△ABC中,D、E是BC边上的两点,若S△ADE= S△ABC,则DE与BC的数量关系是2
.
(2) [问题延伸]如图3,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC的长
度为6,求四边形ABCD的面积.
26.(10分)如图,△ABC是边长为6的等边三角形,P是AC边上一动点.由点A向点C运动
(P与点A、C不重合),点Q同时以点P相同的速度,由点B向CB延长线方向运动(点Q不
与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.
(1)若设AP的长为x,则PC= ,QC= .
(2)当∠BQD=30°时,求AP的长;
(3)点P,Q在运动过程中,线段ED的长是否发生变化?如果不变,求出线段ED的长;
如果变化,请说明理由.
4
{#{QQABDQwyEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
一、单选题(每题3分,共30分)
1.下列说法错误的是( ).
A.关于某条直线对称的两个三角形一定全等 B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称 D.角是关于它的平分线所在直线对称的图形
2.满足下列条件的三角形,不一定是等边三角形的是( ).
A.有两个内角是 60°的三角形 B.有两边相等且是轴对称图形的三角形
C.有一个内角是 60°且是轴对称图形的三角形 D.三边都相等的三角形
3.在联合会上,有 A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在
他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC
的( ).
A.三边中线的交点 B.三条角平分线交点 C.三边中垂线的交点 D.三边上高交点
4.已知△ABC,下列尺规作图的方法中,能确定∠BAD=∠CAD的是( ).
A. B. C. D.
5.如图,在△ABC中,∠C=90°,若 BC=10,AD平分∠BAC交 BC于点 D;且 BD∶CD=3∶2,则点
D到线段 AB的距离 DE为( ).
A.2 B.4 C.5 D.6
6.如图,直线 m∥n,Rt△ABC的顶点 A在直线 n上,∠C=90°,AB,CB分别交直线 m于点 D和点 E,
且 DB=DE,若∠B=25°,则∠1的度数为( ).
A.60° B.65° C.70° D.75°
第 5题图 第 6题图 第 7题图
7.如图,在△ABC中,∠A=90°,AB=6,AC=8,BC=10,CD平分∠BCA交 AB于点 D,点 P,Q
分别是 CD,AC上的动点,连接 AP,PQ,则 AP+PQ的最小值是( ).
A.6 B.5 C.4.8 D.4
8.如图,△ACB≌△DEB,点 A和点 D是对应顶点,∠C=∠E=90°,记∠CBE=α,∠CAB=β,当
AD∥BC时,α与β之间的数量关系为( ).
A.α=2β B.α=β C.a+β=90° D.α+β=180°
9.如图,∠A=∠B=90°,AB=60,E、F分别为线段 AB和射线 BD上的一点,若点 E从点 B出发向
点 A运动,同时点 F从点 B出发向点 D运动,二者速度之比为 3∶7,运动到某时刻同时停止,在射
线 AC上取一点 G,使△AEG与△BEF全等,则 AG的长为( ).
A.18 B.88 C.88或 62 D.18或 70
10.如图,已知△ABC和△CDE都是等边三角形,且 A、C、E三点共线 AD与 BE交于点 O, AD与 BC
交于点 P,BE 与 CD交于点 Q,连接 PQ.以下五个结论:① AD=BE:② ∠ADB=60°;③ AP=
1
{#{QQABDQywEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
BQ;④ △PCQ是等边三角形;⑤ PQ∥AE,其中正确结论的个数有( ).
A.5 B.4 C.3 D.2
第 8题图 第 9题图 第 10题图
二、填空题(每空2分,共16分)
11.如图,△ABC≌△DEF,若∠B=∠C=72°,则∠D的度数为 °.
12.如图,在 Rt△ABC中,∠ACB=90°,OC是斜边 AB上的中线,AB=8,则 OC的长是 .
第 11题图 第 12题图 第 13题图 第 15题图
13.如图,在 4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正
方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形,可供选择的白色小正方形有 个.
14.直角三角形斜边上高线和中线分别是 4和 5,则它的面积是 .
15.如图,球沿图中箭头方向击出后碰到桌子的边缘会反弹,其中∠1叫做入射角,∠2叫做反射角,如果
每次的入射角总是等于反射角,那么球最后将落入桌子四个顶角处的球袋中的 .
16.如图,△ABC中,BD平分∠ABC,BC 的中垂线交 BC 于点 E,交 BD于点 F,连接 CF,若∠A=
60°,∠ABD=24°,则∠ACF= °.
17.如图,点 A、B、C、D均在正方形网格格点上,则∠ABC+∠ADC= °.
第 16题图 第 17题图 第 18题图
18.如图,在 Rt△ABC中,∠ABC=90°,以 AC为边,作△ACD,满足 AD=AC,点 E为 BC上一点,
连接 AE,2∠BAE=∠CAD,连接 DE.若 BE=a,CE=b,则 DE= .
三、解答题(共54分) (用含a、 b的代数式表示)
19.(6分)(1)用尺规作图作一点P,使P至M,N的距离相等,且到AB,BC的距离相等;
(2)在BC上找一点Q,使QM+QN最小.(保留作图痕迹)
(1) (2)
2
{#{QQABDQywEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
20.(4分)如图,点B、F、C、E四点在同条直线上,∠B=∠E,AB=DE,BF=CE.
求证:∠A=∠D.
21.(6分)如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作BC的平行线与AB,
AC分别相交于点M、N.求证:MN=BM+CN.
22.(6分)已知,如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点.
求证:(1)BM=DM;(2)MN⊥BD.
23.(6分)如图所示,∠A=∠B=90°,P是AB的中点,且DP平分∠ADC,连接PC.
(1)试说明CP平分∠BCD;
(2)线段PD与PC有怎样的位置关系?请说明理由.
24.(8分)如图,已知△ABC,AB=AC,∠B=50°,点D在线段BC上,点E在线段AC上,
设∠BAD=α,∠CDE=β.
(1)如果a=20°,β=10°,那么△ADE是等边三角形?请说明理由;
(2)若AD=AE,试求α与β之间的关系.
3
{#{QQABDQywEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
25.(8分)
(1) [问题发现]
① 如图1,△ABC中,AB=AC,D为BC边上的中点,连接AD.设△ABD的面积和
周长分别为S1和C1,△ACD的面积和周长分别为S2和C2,则S1 S2,C1 C2.
(填“>”,“<”或“=”)
1
② 如图2,△ABC中,D、E是BC边上的两点,若S△ADE= S△ABC,则DE与BC的数量关系是2
.
(2) [问题延伸]如图3,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC的长
度为6,求四边形ABCD的面积.
26.(10分)如图,△ABC是边长为6的等边三角形,P是AC边上一动点.由点A向点C运动
(P与点A、C不重合),点Q同时以点P相同的速度,由点B向CB延长线方向运动(点Q不
与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.
(1)若设AP的长为x,则PC= ,QC= .
(2)当∠BQD=30°时,求AP的长;
(3)点P,Q在运动过程中,线段ED的长是否发生变化?如果不变,求出线段ED的长;
如果变化,请说明理由.
4
{#{QQABDQwyEogxgigAwAkIIBTAACQQh5CqQw00c4CUEgAQkkJAOGhALAcgQMgROVxECABMKAMRACAyAJSFRAFBAKBAC=A}#=}}#}
同课章节目录
