人教版初二数学全等三角形中等难度习题一(含解析)
文档属性
| 名称 | 人教版初二数学全等三角形中等难度习题一(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 917.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 13:25:07 | ||
图片预览



文档简介
人教版初二数学全等三角形中等难度习题一
一、单选题
1.如图,方格纸中的和的大小关系是( )
A. B. C. D.
2.如图,在四边形中,对角线平分,,下列结论正确的是( )
A. B.
C. D.与的大小关系不确定
3.在中,已知,、分别是边、上的点,且,,,则等于( ).
A. B. C. D.
二、填空题
4.已知,△ABC中,∠BAC=120°,AD平分∠BAC,∠BDC=60°,AB=2,AC=3,则AD的长是 .
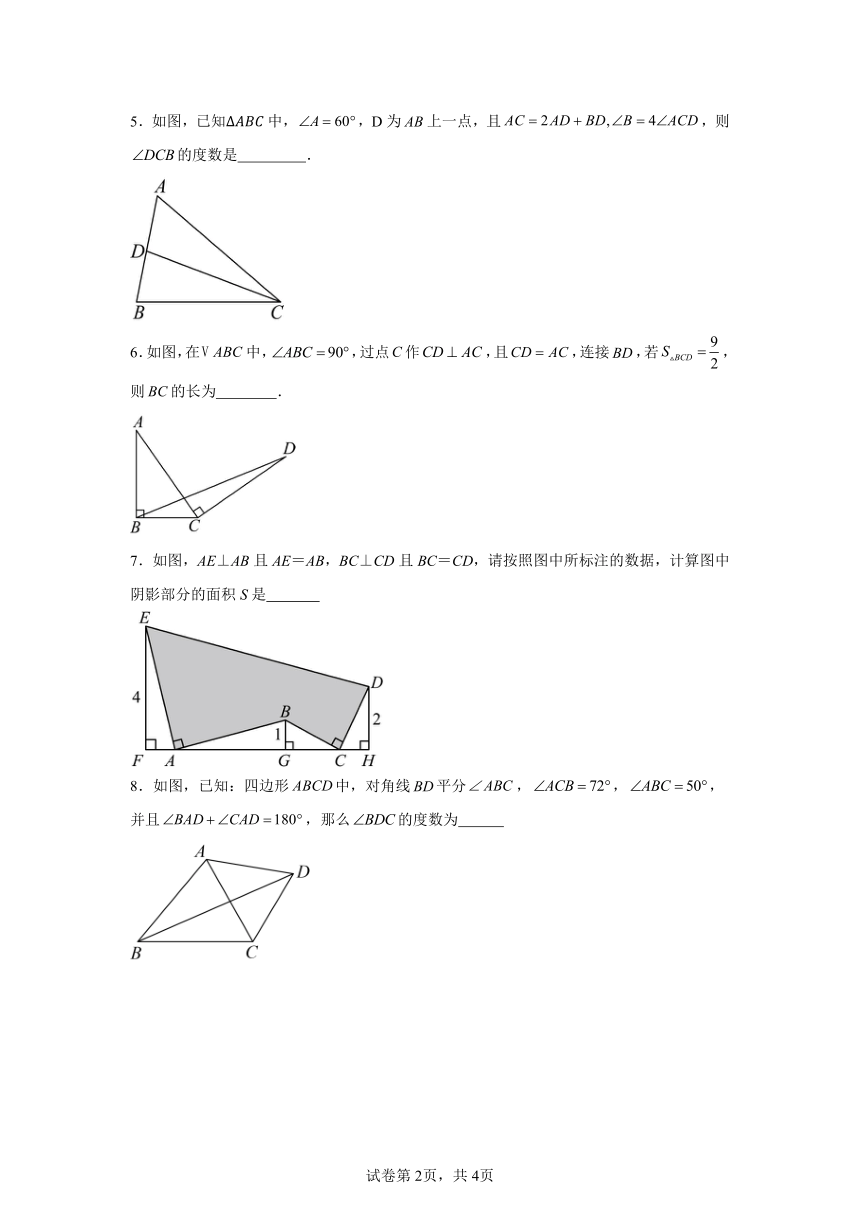
5.如图,已知中,,D为上一点,且,则的度数是 .
6.如图,在中,,过点作,且,连接,若,则的长为 .
7.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中阴影部分的面积S是
8.如图,已知:四边形中,对角线平分,,,并且,那么的度数为
9.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,则∠D= .
10.如图,已知和,,.连接,点F是中点,连接并延长交于点H,已知,,则 .
三、解答题
11.如图,已知:,,的平分线交于点,过作于点, 求证:
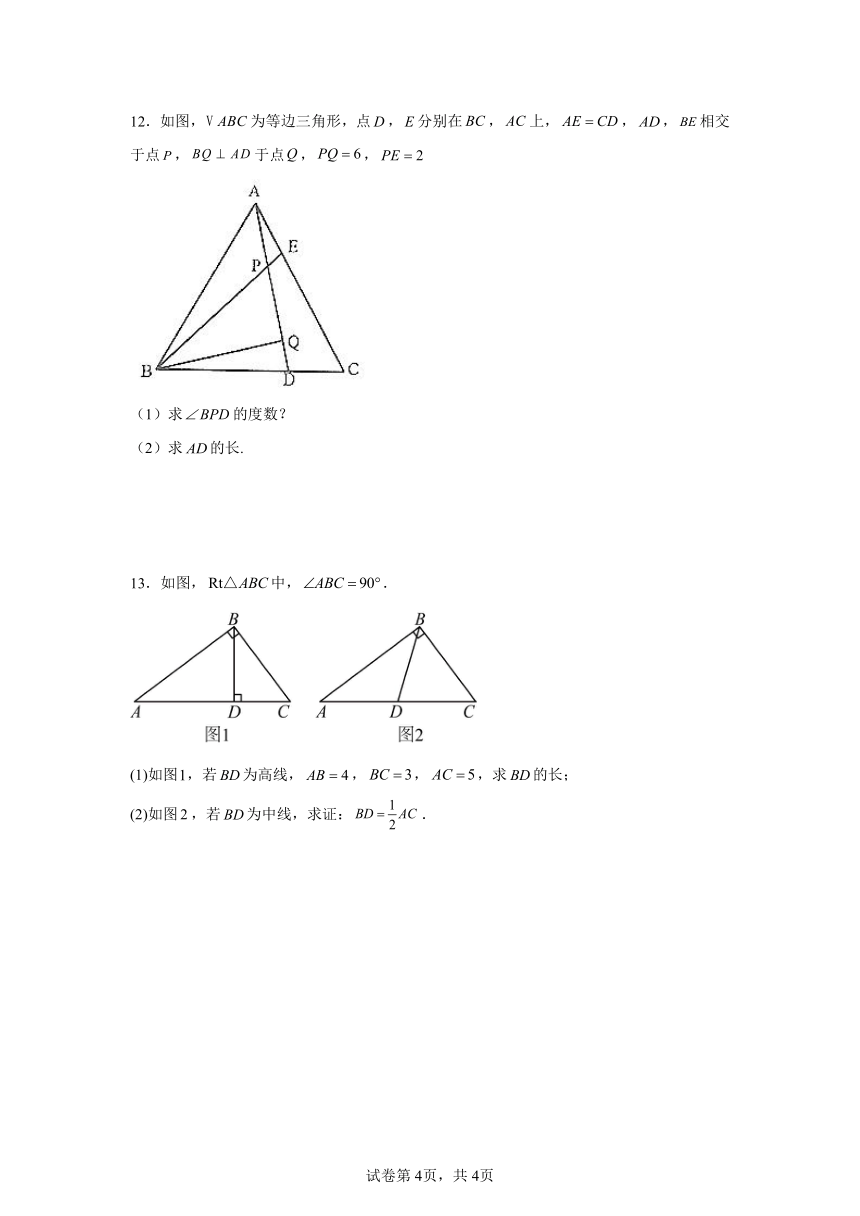
12.如图,为等边三角形,点,分别在,上,,,相交于点,于点,,
(1)求的度数?
(2)求的长.
13.如图,中,.
(1)如图,若为高线,,,,求的长;
(2)如图,若为中线,求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】解:如图,由图可知:,
∴, ∴,
∴.
故选D.
2.A
【详解】解:如图,在AB上取,
对角线平分,,
在和中,,,
,,.
故选:.
3.B
【详解】延长AB到F使BF=AD,连接CF,如图,
∵∠CAD=60°,∠AED=60°,∴△ADE为等边三角形,
∴AD=DE=AE,∠ADE=60°,
∴∠BDE=180°-∠ADE=120°,∵∠CDB=2∠CDE,
∴3∠CDE=120°,解得∠CDE=40°,∴∠CDB=2∠CDE=80°,
∵BF=AD,∴BF=DE,∵DE+BD=CE,∴BF+BD=CE,即DF=CE,
∵AF=AD+DF,AC=AE+CE,∴AF=AC,而∠BAC=60°,∴△AFC为等边三角形,
∴CF=AC,∠F=60°,在△ACD和△FCB 中 ,∴△ACD≌△FCB (SAS),
∴CB=CD,
∴∠CBD=∠CDB=80°,
∴∠DCB=180-(∠CBD+∠CDB)=20°.
故选B.
4.5
【详解】过D作,,交延长线于F,
∵AD平分,,,
∴,,
∵,
,
∴,
∵,
∴,
在和中,∴,∴,
在和中,,∴,∴,
∵,∴,
∴,∴,
∴,∵平分,∴,
∴,
∴.
5.20°
【详解】解:如图,延长至点E使,连接.
∴,∵,∴.
∵,∴是等边三角形,∴,∵,
∴设,则.在与中,∵,∴,
∴.∵,∴,∴,
∴.
故答案是.
6.3
【详解】解:过点作交延长线于点,则∠DMC=90°=∠ABC,
,,,,
,,,,
,.
故填.
7.18
【详解】解:,,,
,,,
,在和中,,
,,
同理,,,
梯形的面积是,
阴影部分的面积是
.
故答案为18.
8.
【详解】解:延长和,过点作于点,过点作于点,
是的平分线
在与中,,,,
又,为的平分线,
过点作于点,在与中,,,
,
.
在与中,
,
为的平分线
,
在中,
,,
,
,
,
.
故答案为:.
9.30°
【详解】试题解析:(1)连接CE,
∵△ABC是等边三角形,
∴AC=BC,
在△BCE与△ACE中,
∴△BCE≌△ACE(SSS)
∴∠BCE=∠ACE=30°
∵BE平分∠DBC,
∴∠DBE=∠CBE,
在△BDE与△BCE中,
∴△BDE≌△BCE(SAS),
∴∠BDE=∠BCE=30°.
10.
【详解】如图所示,延长到点G,使,连接,,
∴
∵,,∴
∴,∵∴∵∴
∴∴∵
∴∴
∴在和中 ∴
∴,,
∵
∴
∴
∴∴∵∴
∵
∴
∴
∴,即
解得. 故答案为:.
11.见解析
【详解】解:∵的平分线交于点,
∴,
∵过作于点,
∴,
∴在和中,,∴,∴,∴,
∵,
∴,
,
∴,
∵,,
∴,
∴在和中,
,
∴,
∴,
∴,
12.(1)60°;(2)14.
【详解】(1)∵△ABC是等边三角形,
∴∠BAE=∠C=60°,AB=AC,
又∵AE=CD,
∴△ABE≌△CAD(SAS)
∴∠CAD=∠ABE,
∵∠AEB=180°-∠ABE-60°,
∴∠APE=180°-(∠CAD+∠AEB)=180°-(∠CAD+180°-∠ABE-60°)=60°.
∴∠BPD=∠APE=60°.
(2)∵BQ⊥AD,∠BPD=60°,
∴∠PBQ=30°,
∵PQ=6,
∴BP=12,
∴BE=BP+PE=12+2=14.
∴AD=BE=14.
13.(1);(2)见解析.
【详解】(1)∵,,,,
∴,∴;
(2)如图,延长至,且使,连接,
在与中,∴,
∴,,
∴,
∵,
∴,在和中,∴,
∴,∴.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,方格纸中的和的大小关系是( )
A. B. C. D.
2.如图,在四边形中,对角线平分,,下列结论正确的是( )
A. B.
C. D.与的大小关系不确定
3.在中,已知,、分别是边、上的点,且,,,则等于( ).
A. B. C. D.
二、填空题
4.已知,△ABC中,∠BAC=120°,AD平分∠BAC,∠BDC=60°,AB=2,AC=3,则AD的长是 .
5.如图,已知中,,D为上一点,且,则的度数是 .
6.如图,在中,,过点作,且,连接,若,则的长为 .
7.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中阴影部分的面积S是
8.如图,已知:四边形中,对角线平分,,,并且,那么的度数为
9.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,则∠D= .
10.如图,已知和,,.连接,点F是中点,连接并延长交于点H,已知,,则 .
三、解答题
11.如图,已知:,,的平分线交于点,过作于点, 求证:
12.如图,为等边三角形,点,分别在,上,,,相交于点,于点,,
(1)求的度数?
(2)求的长.
13.如图,中,.
(1)如图,若为高线,,,,求的长;
(2)如图,若为中线,求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】解:如图,由图可知:,
∴, ∴,
∴.
故选D.
2.A
【详解】解:如图,在AB上取,
对角线平分,,
在和中,,,
,,.
故选:.
3.B
【详解】延长AB到F使BF=AD,连接CF,如图,
∵∠CAD=60°,∠AED=60°,∴△ADE为等边三角形,
∴AD=DE=AE,∠ADE=60°,
∴∠BDE=180°-∠ADE=120°,∵∠CDB=2∠CDE,
∴3∠CDE=120°,解得∠CDE=40°,∴∠CDB=2∠CDE=80°,
∵BF=AD,∴BF=DE,∵DE+BD=CE,∴BF+BD=CE,即DF=CE,
∵AF=AD+DF,AC=AE+CE,∴AF=AC,而∠BAC=60°,∴△AFC为等边三角形,
∴CF=AC,∠F=60°,在△ACD和△FCB 中 ,∴△ACD≌△FCB (SAS),
∴CB=CD,
∴∠CBD=∠CDB=80°,
∴∠DCB=180-(∠CBD+∠CDB)=20°.
故选B.
4.5
【详解】过D作,,交延长线于F,
∵AD平分,,,
∴,,
∵,
,
∴,
∵,
∴,
在和中,∴,∴,
在和中,,∴,∴,
∵,∴,
∴,∴,
∴,∵平分,∴,
∴,
∴.
5.20°
【详解】解:如图,延长至点E使,连接.
∴,∵,∴.
∵,∴是等边三角形,∴,∵,
∴设,则.在与中,∵,∴,
∴.∵,∴,∴,
∴.
故答案是.
6.3
【详解】解:过点作交延长线于点,则∠DMC=90°=∠ABC,
,,,,
,,,,
,.
故填.
7.18
【详解】解:,,,
,,,
,在和中,,
,,
同理,,,
梯形的面积是,
阴影部分的面积是
.
故答案为18.
8.
【详解】解:延长和,过点作于点,过点作于点,
是的平分线
在与中,,,,
又,为的平分线,
过点作于点,在与中,,,
,
.
在与中,
,
为的平分线
,
在中,
,,
,
,
,
.
故答案为:.
9.30°
【详解】试题解析:(1)连接CE,
∵△ABC是等边三角形,
∴AC=BC,
在△BCE与△ACE中,
∴△BCE≌△ACE(SSS)
∴∠BCE=∠ACE=30°
∵BE平分∠DBC,
∴∠DBE=∠CBE,
在△BDE与△BCE中,
∴△BDE≌△BCE(SAS),
∴∠BDE=∠BCE=30°.
10.
【详解】如图所示,延长到点G,使,连接,,
∴
∵,,∴
∴,∵∴∵∴
∴∴∵
∴∴
∴在和中 ∴
∴,,
∵
∴
∴
∴∴∵∴
∵
∴
∴
∴,即
解得. 故答案为:.
11.见解析
【详解】解:∵的平分线交于点,
∴,
∵过作于点,
∴,
∴在和中,,∴,∴,∴,
∵,
∴,
,
∴,
∵,,
∴,
∴在和中,
,
∴,
∴,
∴,
12.(1)60°;(2)14.
【详解】(1)∵△ABC是等边三角形,
∴∠BAE=∠C=60°,AB=AC,
又∵AE=CD,
∴△ABE≌△CAD(SAS)
∴∠CAD=∠ABE,
∵∠AEB=180°-∠ABE-60°,
∴∠APE=180°-(∠CAD+∠AEB)=180°-(∠CAD+180°-∠ABE-60°)=60°.
∴∠BPD=∠APE=60°.
(2)∵BQ⊥AD,∠BPD=60°,
∴∠PBQ=30°,
∵PQ=6,
∴BP=12,
∴BE=BP+PE=12+2=14.
∴AD=BE=14.
13.(1);(2)见解析.
【详解】(1)∵,,,,
∴,∴;
(2)如图,延长至,且使,连接,
在与中,∴,
∴,,
∴,
∵,
∴,在和中,∴,
∴,∴.
答案第1页,共2页
答案第1页,共2页
