人教版2024-2025学年八年级数学第11章 三角形 单元检测卷(含答案)
文档属性
| 名称 | 人教版2024-2025学年八年级数学第11章 三角形 单元检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 06:24:50 | ||
图片预览




文档简介
人教版2024-2025学年八年级数学第11章 三角形 单元检测卷
班级: 姓名:
亲爱的同学们:
练习开始了,希望你认真审题,细致做题,不断探索数学知识,领略数学的美妙风景。运用所学知识解决本练习,祝你学习进步!
一、单选题(每题3分,共30分)
1.现有两根木棒,它们的长分别是和,若要钉一个三角架,则下列四根木棒的长度应选( )
A. B. C. D.
2.学习了三角形的“中线、高线、角平分线”后,老师给同学们布置了一项作业:作的边上的高.下面是四位同学的作业,其中正确的是( )
A. B.
C. D.
3.如图,在中,,,是的一条角平分线,则的度数为( )
A. B. C. D.
4.如图,将空调安装在墙上时,一般都会采用如图所示的方法固定,这种做法的依据是( )
A.垂线段最短 B.两点确定一条直线
C.两点之间,线段最短 D.三角形的稳定性
5.如图,,,平分,过点作于点,则的度数是( )
A. B. C. D.
6.如图,,则的度数为( )
A. B. C. D.
7.一副直角三角板按如图所示的方式摆放,点在的延长线上,当时,的度数为( )
A. B. C. D.
8.“转化”是数学中的一种重要思想方法,同学们在研究多边形(边数大于3)的内角和度数时,通常是将多边形的内角和转化为三角形的内角和来解决,从而化陌生的问题为熟悉的情境来解决问题.现从某边形一边上的一点(不包含端点)出发,依次连接多边形的各个顶点,分割得到的所有三角形的内角和是,则该边形是( )边形.
A.五 B.六 C.七 D.八
9.如图,( )
A. B. C. D.
10.正四边形与其他正多边形组合可以铺设地板,则该多边形可以是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
二、填空题(每题3分,共15分)
11.如图,在△ABC中,点D、E分别是BC、AB边上的中点,若△ADE的面积是2,则△ABC的面积是 .
12.如图,在 中,,过点作,若,则等于 度.
13.如图,用铁丝折成一个四边形ABCD(点C在直线BD的上方),且∠A=70°,∠BCD=120°,若使∠ABC、∠ADC平分线的夹角∠E的度数为100°,可保持∠A不变,将∠BCD (填“增大”或“减小”) °.
14.如图,从五边形的某个顶点出发可以引 条对角线,若、、、、为该五边形的五个内角,则这五个内角之和为 °.
15.一个多边形每个外角的度数都为,它的内角和度数为 .
三、解答题(共8题,共55分)
16.已知一个等腰三角形的腰长为x,底边长为y,周长为11.
(1)写出y与x的关系式为______;
(2)若,请求出符合条件的整数x的值.
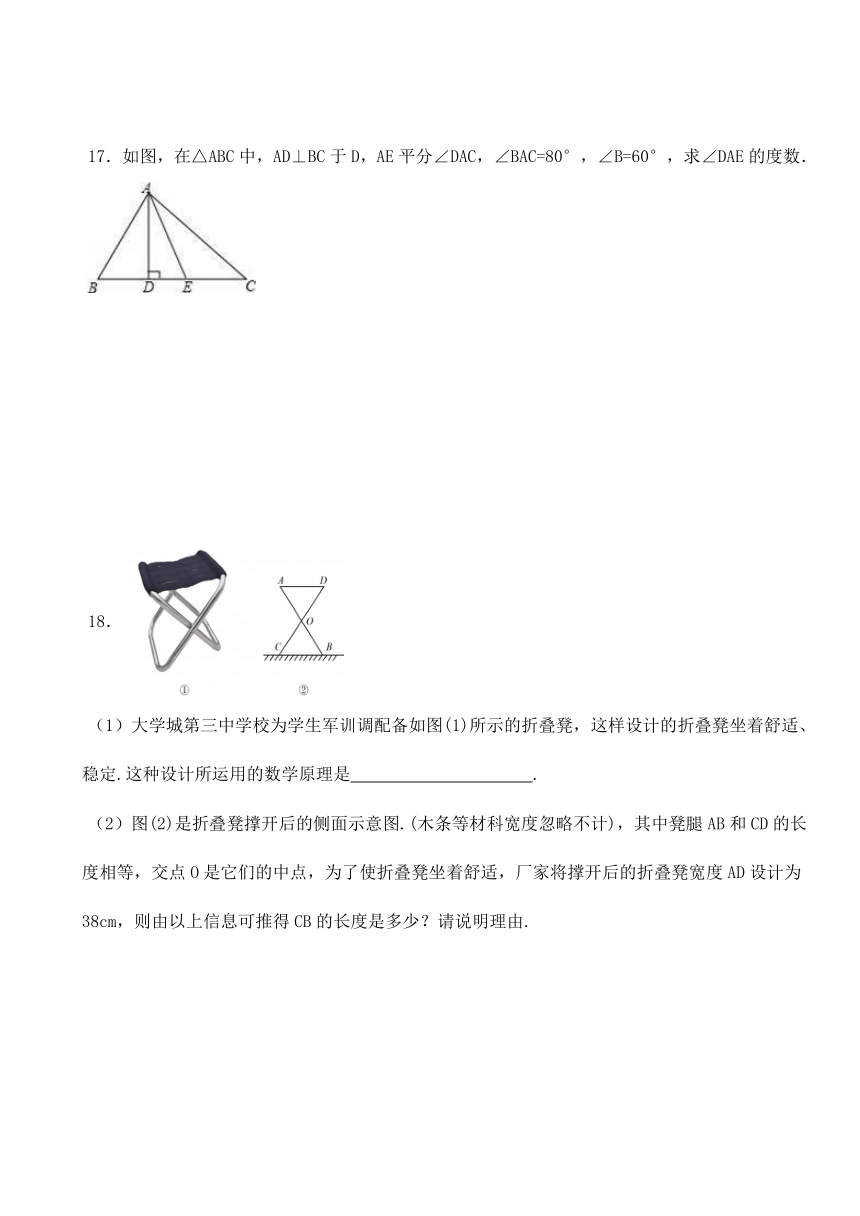
17.如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠DAE的度数.
18.
(1)大学城第三中学校为学生军训调配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 .
(2)图(2)是折叠凳撑开后的侧面示意图.(木条等材科宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
19.如图,在中,点是边上的一点,连接.
(1)若,,求的度数;
(2)若平分,,,试说明:.
20.如图,中,于点D,BE是的平分线,若,.求的度数.
21.
(1)如图①,△ABC中,点D,E在边BC上,AD平分∠BAC,AE⊥BC, , ,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其他条件不变,求∠F的度数.
22.阅读明明和芳芳的对话,解答下列问题.
(1)明明通过计算,发现少加了一个锐角,则这个“少加的锐角”的度数是__________.
(2)明明求的是几边形的内角和?
(3)这个多边形对角线的总条数是__________.
23.“转化”是数学中的一种重要思想,即把陌生的问题转化为熟悉的问题,把复杂的问题转化为简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图①中的度数;
(2)若将图①中的星形截去一个角,如图②,请你求出的度数;
(3)若再将图②中的星形进一步截去角,你能由题(2)中所得的方法或规律,猜想出图③中的的度数吗?(只要写出结论,不需要写出解题过程)
答案解析部分
1.答案:B
2.答案:A
3.答案:A
4.答案:D
5.答案:A
6.答案:D
7.答案:B
8.答案:D
9.答案:B
10.答案:C
11.答案:8
12.答案:35
13.答案:增大;10
14.答案:2;540
15.答案:
16.答案:(1)y=11-2x();
(2)3,4
17.答案:解:在△ABC中,∵∠BAC+∠B+∠C=180°,
∴∠C=180°-80°-60°=40°,
∵AD⊥BC于D,
∴∠ADC=90°,在△ADC中,∠DAC=90°-∠C=90°-40°=50°,
∵AE平分∠DAC,
∴∠DAE= ∠DAC=25°
18.答案:(1)三角形具有稳定性
(2)解:∵O是AB和CD的中点
∴A0=B0,CO=DO
在△AOD和△BOC中
∴△AOD≌△BOC(SAS)
又∵AD=38cm,
∴BC=AD=38cm.
19.答案:(1)解:∵,,
又∵,
∴,
∴,
∴的度数为;
(2)证明:∵,,
∴,
∵平分,
∴,
∴,
∴,
∴.
20.答案:解:∵∠BAC=80°,∠DAC=30°,
∴∠BAD=∠BAC-∠DAC=50°
∵AD⊥BC,
∴∠ADB=90°
∴∠ABD=180°-∠ADB-∠BAD
=180°-90°-50°
=40°
∵BE是△ABC的平分线,
∴∠EBA=∠ABC=20°;
∴∠AOB=180°-∠BAO-∠ABO
=180°-50°-20°
=110°
21.答案:(1)解:
∵AD平分∠BAC,
,
,
,
,
;
(2)解:作AH⊥BC于H,如图②,
由(1)可得,
,
,
;
22.答案:(1)20
(2)明明求的是八边形的内角和
(3)20
23.答案:(1)
(2)
(3)
班级: 姓名:
亲爱的同学们:
练习开始了,希望你认真审题,细致做题,不断探索数学知识,领略数学的美妙风景。运用所学知识解决本练习,祝你学习进步!
一、单选题(每题3分,共30分)
1.现有两根木棒,它们的长分别是和,若要钉一个三角架,则下列四根木棒的长度应选( )
A. B. C. D.
2.学习了三角形的“中线、高线、角平分线”后,老师给同学们布置了一项作业:作的边上的高.下面是四位同学的作业,其中正确的是( )
A. B.
C. D.
3.如图,在中,,,是的一条角平分线,则的度数为( )
A. B. C. D.
4.如图,将空调安装在墙上时,一般都会采用如图所示的方法固定,这种做法的依据是( )
A.垂线段最短 B.两点确定一条直线
C.两点之间,线段最短 D.三角形的稳定性
5.如图,,,平分,过点作于点,则的度数是( )
A. B. C. D.
6.如图,,则的度数为( )
A. B. C. D.
7.一副直角三角板按如图所示的方式摆放,点在的延长线上,当时,的度数为( )
A. B. C. D.
8.“转化”是数学中的一种重要思想方法,同学们在研究多边形(边数大于3)的内角和度数时,通常是将多边形的内角和转化为三角形的内角和来解决,从而化陌生的问题为熟悉的情境来解决问题.现从某边形一边上的一点(不包含端点)出发,依次连接多边形的各个顶点,分割得到的所有三角形的内角和是,则该边形是( )边形.
A.五 B.六 C.七 D.八
9.如图,( )
A. B. C. D.
10.正四边形与其他正多边形组合可以铺设地板,则该多边形可以是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
二、填空题(每题3分,共15分)
11.如图,在△ABC中,点D、E分别是BC、AB边上的中点,若△ADE的面积是2,则△ABC的面积是 .
12.如图,在 中,,过点作,若,则等于 度.
13.如图,用铁丝折成一个四边形ABCD(点C在直线BD的上方),且∠A=70°,∠BCD=120°,若使∠ABC、∠ADC平分线的夹角∠E的度数为100°,可保持∠A不变,将∠BCD (填“增大”或“减小”) °.
14.如图,从五边形的某个顶点出发可以引 条对角线,若、、、、为该五边形的五个内角,则这五个内角之和为 °.
15.一个多边形每个外角的度数都为,它的内角和度数为 .
三、解答题(共8题,共55分)
16.已知一个等腰三角形的腰长为x,底边长为y,周长为11.
(1)写出y与x的关系式为______;
(2)若,请求出符合条件的整数x的值.
17.如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠DAE的度数.
18.
(1)大学城第三中学校为学生军训调配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 .
(2)图(2)是折叠凳撑开后的侧面示意图.(木条等材科宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
19.如图,在中,点是边上的一点,连接.
(1)若,,求的度数;
(2)若平分,,,试说明:.
20.如图,中,于点D,BE是的平分线,若,.求的度数.
21.
(1)如图①,△ABC中,点D,E在边BC上,AD平分∠BAC,AE⊥BC, , ,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其他条件不变,求∠F的度数.
22.阅读明明和芳芳的对话,解答下列问题.
(1)明明通过计算,发现少加了一个锐角,则这个“少加的锐角”的度数是__________.
(2)明明求的是几边形的内角和?
(3)这个多边形对角线的总条数是__________.
23.“转化”是数学中的一种重要思想,即把陌生的问题转化为熟悉的问题,把复杂的问题转化为简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图①中的度数;
(2)若将图①中的星形截去一个角,如图②,请你求出的度数;
(3)若再将图②中的星形进一步截去角,你能由题(2)中所得的方法或规律,猜想出图③中的的度数吗?(只要写出结论,不需要写出解题过程)
答案解析部分
1.答案:B
2.答案:A
3.答案:A
4.答案:D
5.答案:A
6.答案:D
7.答案:B
8.答案:D
9.答案:B
10.答案:C
11.答案:8
12.答案:35
13.答案:增大;10
14.答案:2;540
15.答案:
16.答案:(1)y=11-2x();
(2)3,4
17.答案:解:在△ABC中,∵∠BAC+∠B+∠C=180°,
∴∠C=180°-80°-60°=40°,
∵AD⊥BC于D,
∴∠ADC=90°,在△ADC中,∠DAC=90°-∠C=90°-40°=50°,
∵AE平分∠DAC,
∴∠DAE= ∠DAC=25°
18.答案:(1)三角形具有稳定性
(2)解:∵O是AB和CD的中点
∴A0=B0,CO=DO
在△AOD和△BOC中
∴△AOD≌△BOC(SAS)
又∵AD=38cm,
∴BC=AD=38cm.
19.答案:(1)解:∵,,
又∵,
∴,
∴,
∴的度数为;
(2)证明:∵,,
∴,
∵平分,
∴,
∴,
∴,
∴.
20.答案:解:∵∠BAC=80°,∠DAC=30°,
∴∠BAD=∠BAC-∠DAC=50°
∵AD⊥BC,
∴∠ADB=90°
∴∠ABD=180°-∠ADB-∠BAD
=180°-90°-50°
=40°
∵BE是△ABC的平分线,
∴∠EBA=∠ABC=20°;
∴∠AOB=180°-∠BAO-∠ABO
=180°-50°-20°
=110°
21.答案:(1)解:
∵AD平分∠BAC,
,
,
,
,
;
(2)解:作AH⊥BC于H,如图②,
由(1)可得,
,
,
;
22.答案:(1)20
(2)明明求的是八边形的内角和
(3)20
23.答案:(1)
(2)
(3)
