第二十一章 一元二次方程 单元练习(含答案) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十一章 一元二次方程 单元练习(含答案) 2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 296.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 06:42:02 | ||
图片预览

文档简介
第二十一章 一元二次方程 单元练习 2024-2025学年人教版数学九年级上册
一、单选题
1.下列方程中,是关于的一元二次方程的是( )
A. B. C. D.
2.将一元二次方程化为一般形式后,它的各项系数的和为( )
A.6 B.4 C.2 D.
3.已知a,b,c分别是三角形的三边,则方程(a+b)x2+2cx+(a+b)=0的根的情况是( )
A.没有实数根 B.可能有且只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
4.关于x的一元二次方程x2﹣x﹣m2=0的根的情况是( )
A.有两个相等实根 B.有两个不等实根
C.只有一个实根 D.没有实数根
5.已知关于x的一元二次方程有两个不相等的实数根x1,x2.若,则m的值是( )
A.2 B.﹣1 C.2或﹣1 D.不存在
6.如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另三边用总长为55米的栅栏围成,若设栅栏AB的长为x米,则下列各方程中,正确的是( )
A. x(55﹣x)=375 B. x(55﹣2x)=375
C.x(55﹣2x)=375 D.x(55﹣x)=375
7.某社区为改善环境,决定加大绿化投入.四月份绿化投入25万元,四至六月份的绿化总投入将达到109万元,五月份和六月份绿化投入的月平均增长率相同.设五月份和六月份绿化投入的月平均增长率为,根据题意所列方程为( )
A. B.
C. D.
8.若三角形的两边长分别是2和5,第三边的长是方程x2﹣7x+12=0的一个根,则这个三角形的周长是( )
A.10 B.11 C.10或11 D.10或12
9.已知点A,B,C是直线l上互不重合的三个点,设,,,其中n,a是常数,( )
A.若,则点A在点B,C之间
B.若,则点A在点B,C之间
C.若,则点C在点A,B之间
D.若,则点C在点A,B之间
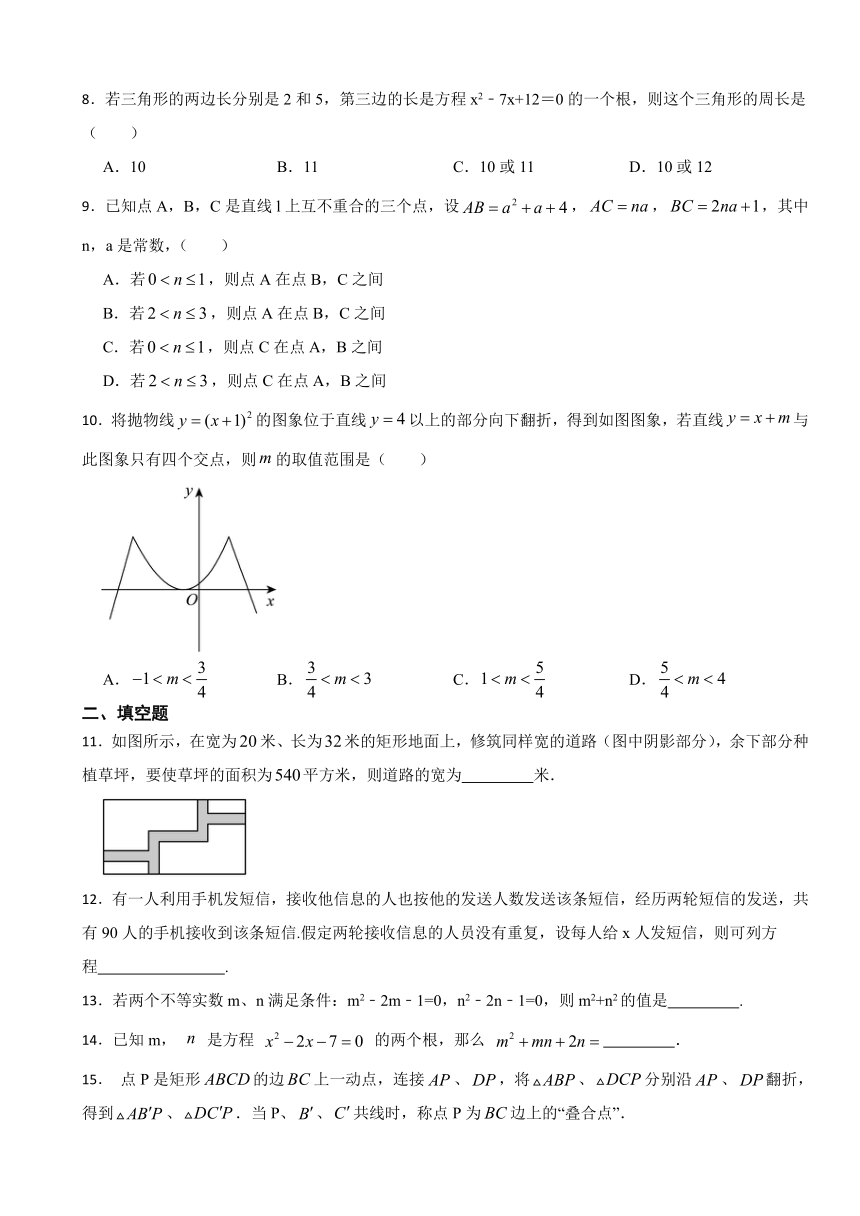
10.将抛物线的图象位于直线以上的部分向下翻折,得到如图图象,若直线与此图象只有四个交点,则的取值范围是( )
A. B. C. D.
二、填空题
11.如图所示,在宽为米、长为米的矩形地面上,修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为平方米,则道路的宽为 米.
12.有一人利用手机发短信,接收他信息的人也按他的发送人数发送该条短信,经历两轮短信的发送,共有90人的手机接收到该条短信.假定两轮接收信息的人员没有重复,设每人给x人发短信,则可列方程 .
13.若两个不等实数m、n满足条件:m2﹣2m﹣1=0,n2﹣2n﹣1=0,则m2+n2的值是 .
14.已知m, 是方程 的两个根,那么 .
15. 点P是矩形的边上一动点,连接、,将、分别沿、翻折,得到、.当P、、共线时,称点P为边上的“叠合点”.
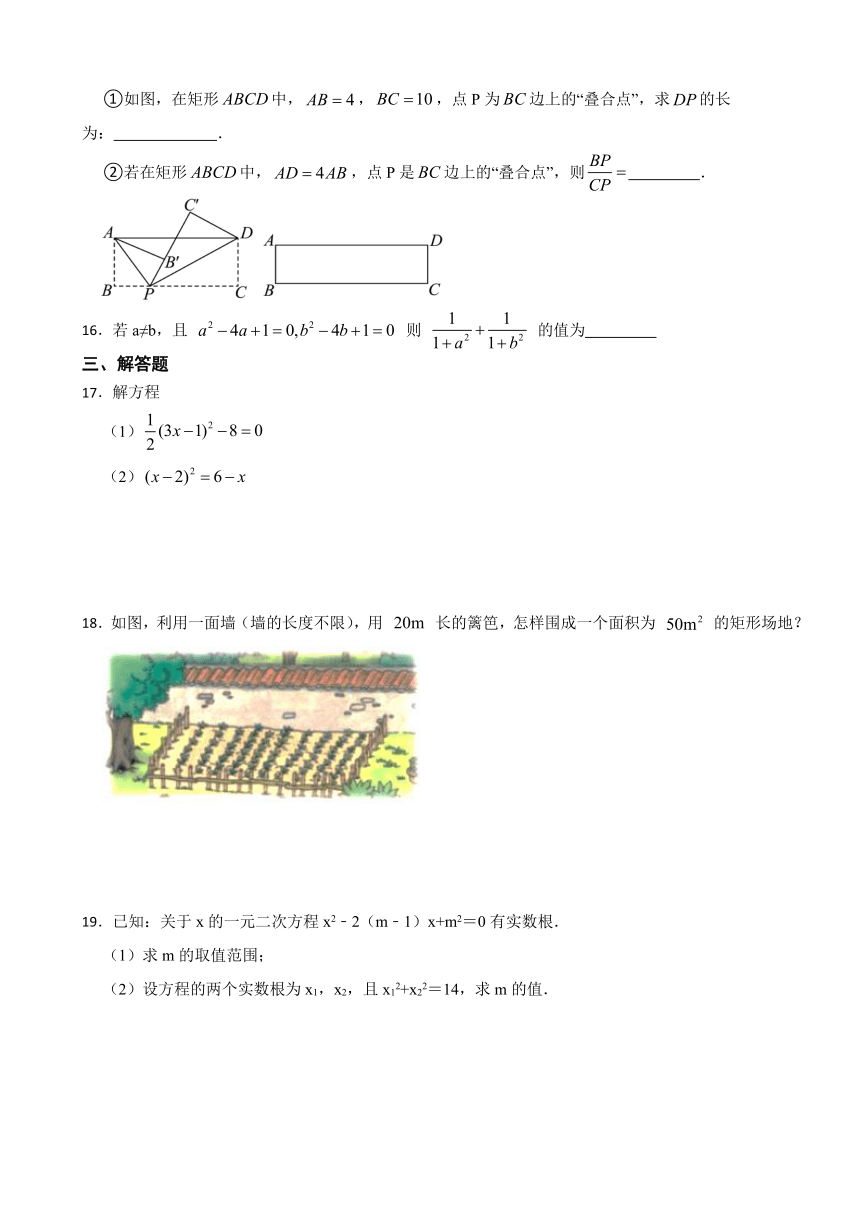
①如图,在矩形中,,,点P为边上的“叠合点”,求的长为: .
②若在矩形中,,点P是边上的“叠合点”,则 .
16.若a≠b,且 则 的值为
三、解答题
17.解方程
(1)
(2)
18.如图,利用一面墙(墙的长度不限),用 长的篱笆,怎样围成一个面积为 的矩形场地?
19.已知:关于x的一元二次方程x2﹣2(m﹣1)x+m2=0有实数根.
(1)求m的取值范围;
(2)设方程的两个实数根为x1,x2,且x12+x22=14,求m的值.
20.某苗圃用花盆培育某种花苗,经过试验发现,每盆植人3株时,平均每株盈利3元.在同样的栽培条件下,若每盆增加1株,平均每株盈利就减少0.5元,要使每盆的盈利为10元,且每盆植入株数尽可能少,每盆应植入多少株?
21.某商店销售一批头盔,售价为每顶80元,每月可售出200顶,在“创建文明城市”期间,计划将头盔降价销售,经调查发现,每降价1元,每月多售出20顶,已知头盔的进价为每顶50元.
(1)若每顶头盔降价10元,则每月可销售 顶头盔,每月销售利润为 元.
(2)若商店为了减少库存,准备降价销售这批头盔,同时确保每月的销售利润为7500元,求头盔的销售单价.
(3)若降价销售这批头盔,每月的利润能否达到9000元?请说明理由.
22.某网店准备销售一种多功能旅行背包,计划从厂家以每个120元的价格进货.
(1)经过市场调查发现,当每个背包的售价为140元时,月均销量为980个,售价每增长10元,月均销量就相应减少30个,若使这种背包的月均销量不低于800个,每个背包售价应不高于多少元?
(2)在实际销售过程中,由于原材料涨价和生产成本增加的原因,每个背包的进价为150元,而每个背包的售价比(1)中最高售价减少了a%(a>0),月均销量比(1)中最低月均销量800个增加了5a%,结果该店销售该背包的月均利润达到了40000元,求在实际销售过程中每个背包售价为多少元?
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】x(1+x)=90
13.【答案】6
14.【答案】4
15.【答案】或;
16.【答案】1
17.【答案】(1),;
(2),.
18.【答案】解:设与墙垂直的篱笆长为xm,则与墙平行的篱笆长为 m,
根据题意,得 ,
整理得, ,
解得 ,
.
答:用20m长的篱笆围成一个长为10 m,宽为5 m的矩形(其中一边长10m,另两边长5 m).
19.【答案】(1);(2)
20.【答案】解:设每盆花苗增加x株,则每盆花苗有 株,
平均单株盈利为: 元,
由题意得: .
化简,整理, .
解这个方程,得 , ,
则 , ,
每盆植入株数尽可能少,
盆应植4株.
答:每盆应植4株.
21.【答案】(1)400;8000
(2)解:设降价元,每月的利润为7500元,
根据题意可得,
化简方程可得,
解得,.
商店要减少库存,
(元).
答:头盔的销售单价为65元.
(3)解:每月的利润不能达到9000元.
理由:设降价元,每月的利润为9000元,
根据题意可得,
化简方程可得
,
原方程无解,
每月的利润不能达到9000元.
22.【答案】(1) 200元;(2) 190元
一、单选题
1.下列方程中,是关于的一元二次方程的是( )
A. B. C. D.
2.将一元二次方程化为一般形式后,它的各项系数的和为( )
A.6 B.4 C.2 D.
3.已知a,b,c分别是三角形的三边,则方程(a+b)x2+2cx+(a+b)=0的根的情况是( )
A.没有实数根 B.可能有且只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
4.关于x的一元二次方程x2﹣x﹣m2=0的根的情况是( )
A.有两个相等实根 B.有两个不等实根
C.只有一个实根 D.没有实数根
5.已知关于x的一元二次方程有两个不相等的实数根x1,x2.若,则m的值是( )
A.2 B.﹣1 C.2或﹣1 D.不存在
6.如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另三边用总长为55米的栅栏围成,若设栅栏AB的长为x米,则下列各方程中,正确的是( )
A. x(55﹣x)=375 B. x(55﹣2x)=375
C.x(55﹣2x)=375 D.x(55﹣x)=375
7.某社区为改善环境,决定加大绿化投入.四月份绿化投入25万元,四至六月份的绿化总投入将达到109万元,五月份和六月份绿化投入的月平均增长率相同.设五月份和六月份绿化投入的月平均增长率为,根据题意所列方程为( )
A. B.
C. D.
8.若三角形的两边长分别是2和5,第三边的长是方程x2﹣7x+12=0的一个根,则这个三角形的周长是( )
A.10 B.11 C.10或11 D.10或12
9.已知点A,B,C是直线l上互不重合的三个点,设,,,其中n,a是常数,( )
A.若,则点A在点B,C之间
B.若,则点A在点B,C之间
C.若,则点C在点A,B之间
D.若,则点C在点A,B之间
10.将抛物线的图象位于直线以上的部分向下翻折,得到如图图象,若直线与此图象只有四个交点,则的取值范围是( )
A. B. C. D.
二、填空题
11.如图所示,在宽为米、长为米的矩形地面上,修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为平方米,则道路的宽为 米.
12.有一人利用手机发短信,接收他信息的人也按他的发送人数发送该条短信,经历两轮短信的发送,共有90人的手机接收到该条短信.假定两轮接收信息的人员没有重复,设每人给x人发短信,则可列方程 .
13.若两个不等实数m、n满足条件:m2﹣2m﹣1=0,n2﹣2n﹣1=0,则m2+n2的值是 .
14.已知m, 是方程 的两个根,那么 .
15. 点P是矩形的边上一动点,连接、,将、分别沿、翻折,得到、.当P、、共线时,称点P为边上的“叠合点”.
①如图,在矩形中,,,点P为边上的“叠合点”,求的长为: .
②若在矩形中,,点P是边上的“叠合点”,则 .
16.若a≠b,且 则 的值为
三、解答题
17.解方程
(1)
(2)
18.如图,利用一面墙(墙的长度不限),用 长的篱笆,怎样围成一个面积为 的矩形场地?
19.已知:关于x的一元二次方程x2﹣2(m﹣1)x+m2=0有实数根.
(1)求m的取值范围;
(2)设方程的两个实数根为x1,x2,且x12+x22=14,求m的值.
20.某苗圃用花盆培育某种花苗,经过试验发现,每盆植人3株时,平均每株盈利3元.在同样的栽培条件下,若每盆增加1株,平均每株盈利就减少0.5元,要使每盆的盈利为10元,且每盆植入株数尽可能少,每盆应植入多少株?
21.某商店销售一批头盔,售价为每顶80元,每月可售出200顶,在“创建文明城市”期间,计划将头盔降价销售,经调查发现,每降价1元,每月多售出20顶,已知头盔的进价为每顶50元.
(1)若每顶头盔降价10元,则每月可销售 顶头盔,每月销售利润为 元.
(2)若商店为了减少库存,准备降价销售这批头盔,同时确保每月的销售利润为7500元,求头盔的销售单价.
(3)若降价销售这批头盔,每月的利润能否达到9000元?请说明理由.
22.某网店准备销售一种多功能旅行背包,计划从厂家以每个120元的价格进货.
(1)经过市场调查发现,当每个背包的售价为140元时,月均销量为980个,售价每增长10元,月均销量就相应减少30个,若使这种背包的月均销量不低于800个,每个背包售价应不高于多少元?
(2)在实际销售过程中,由于原材料涨价和生产成本增加的原因,每个背包的进价为150元,而每个背包的售价比(1)中最高售价减少了a%(a>0),月均销量比(1)中最低月均销量800个增加了5a%,结果该店销售该背包的月均利润达到了40000元,求在实际销售过程中每个背包售价为多少元?
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】x(1+x)=90
13.【答案】6
14.【答案】4
15.【答案】或;
16.【答案】1
17.【答案】(1),;
(2),.
18.【答案】解:设与墙垂直的篱笆长为xm,则与墙平行的篱笆长为 m,
根据题意,得 ,
整理得, ,
解得 ,
.
答:用20m长的篱笆围成一个长为10 m,宽为5 m的矩形(其中一边长10m,另两边长5 m).
19.【答案】(1);(2)
20.【答案】解:设每盆花苗增加x株,则每盆花苗有 株,
平均单株盈利为: 元,
由题意得: .
化简,整理, .
解这个方程,得 , ,
则 , ,
每盆植入株数尽可能少,
盆应植4株.
答:每盆应植4株.
21.【答案】(1)400;8000
(2)解:设降价元,每月的利润为7500元,
根据题意可得,
化简方程可得,
解得,.
商店要减少库存,
(元).
答:头盔的销售单价为65元.
(3)解:每月的利润不能达到9000元.
理由:设降价元,每月的利润为9000元,
根据题意可得,
化简方程可得
,
原方程无解,
每月的利润不能达到9000元.
22.【答案】(1) 200元;(2) 190元
同课章节目录
