2024-2025学年北师大版九年级数学上册第一章 特殊平行四边形 单元测试(含答案)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学上册第一章 特殊平行四边形 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 524.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 08:36:51 | ||
图片预览


文档简介
第一章 特殊平行四边形 单元测试 2024-2025学年北师大版九年级数学上册
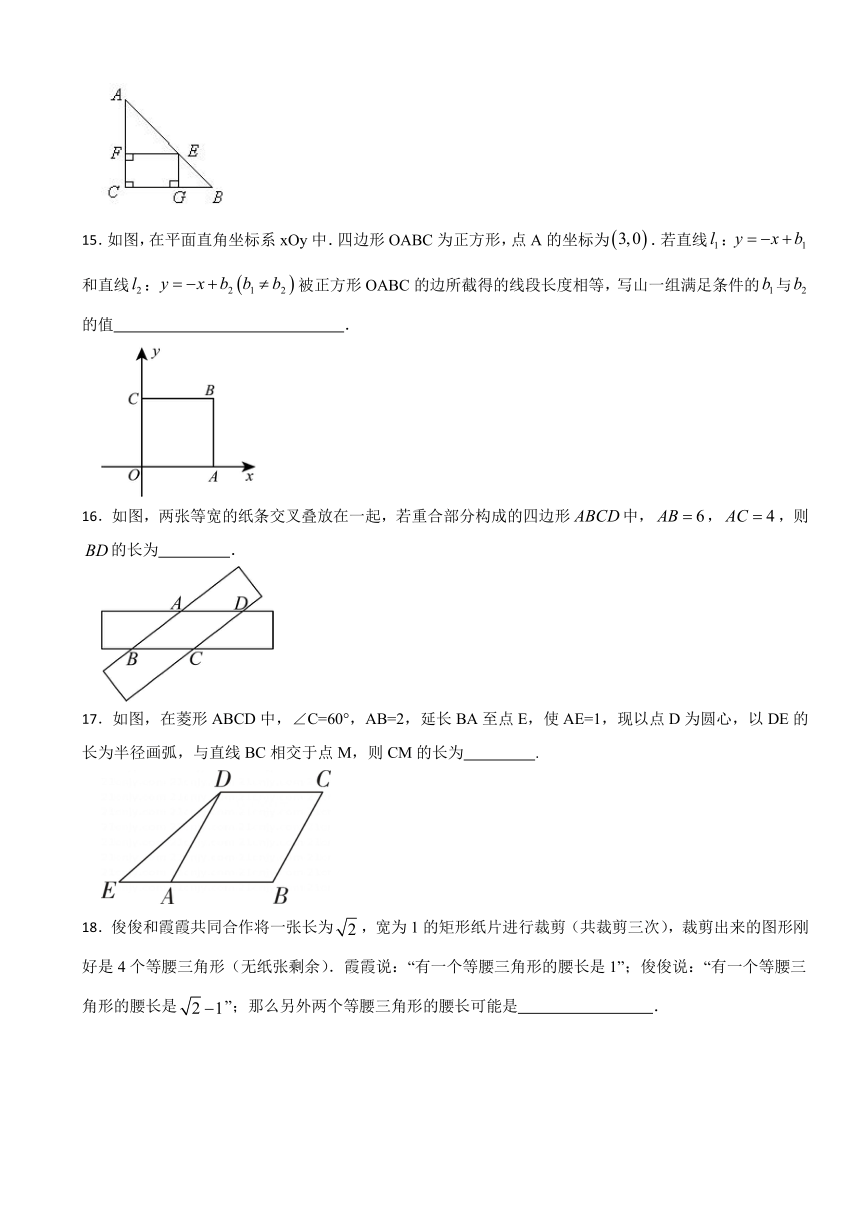
一、单选题
1.两条对角线互相垂直平分的四边形是( )
A.等腰梯形 B.菱形 C.矩形 D.平行四边形
2.如图,平行四边形ABCD的对角线AC,BD相交于点O,添加下列条件仍不能判断四边形ABCD是菱形的是( )
A.AB=AD B.AO2+BO2=AB2
C.AC=BD D.∠BAC=∠ACB
3.如图,为庆祝“五·一”劳动节,某单位要在广场上布置一个矩形的花坛美化环境,计划用红花摆成两条对角线.如果一条对角线用了51盆红花,则另一条对角线还需要红花盆数是( )
A.49盆 B.50盆 C.51盆 D.52盆
4.菱形中,对角线长度分别为6和8,则菱形的面积是( )
A.24 B.12 C.36 D.10
5.如图,正方形的边长为8,点M在上,且,N是上一动点,则的最小值为( ).
A.8 B. C. D.10
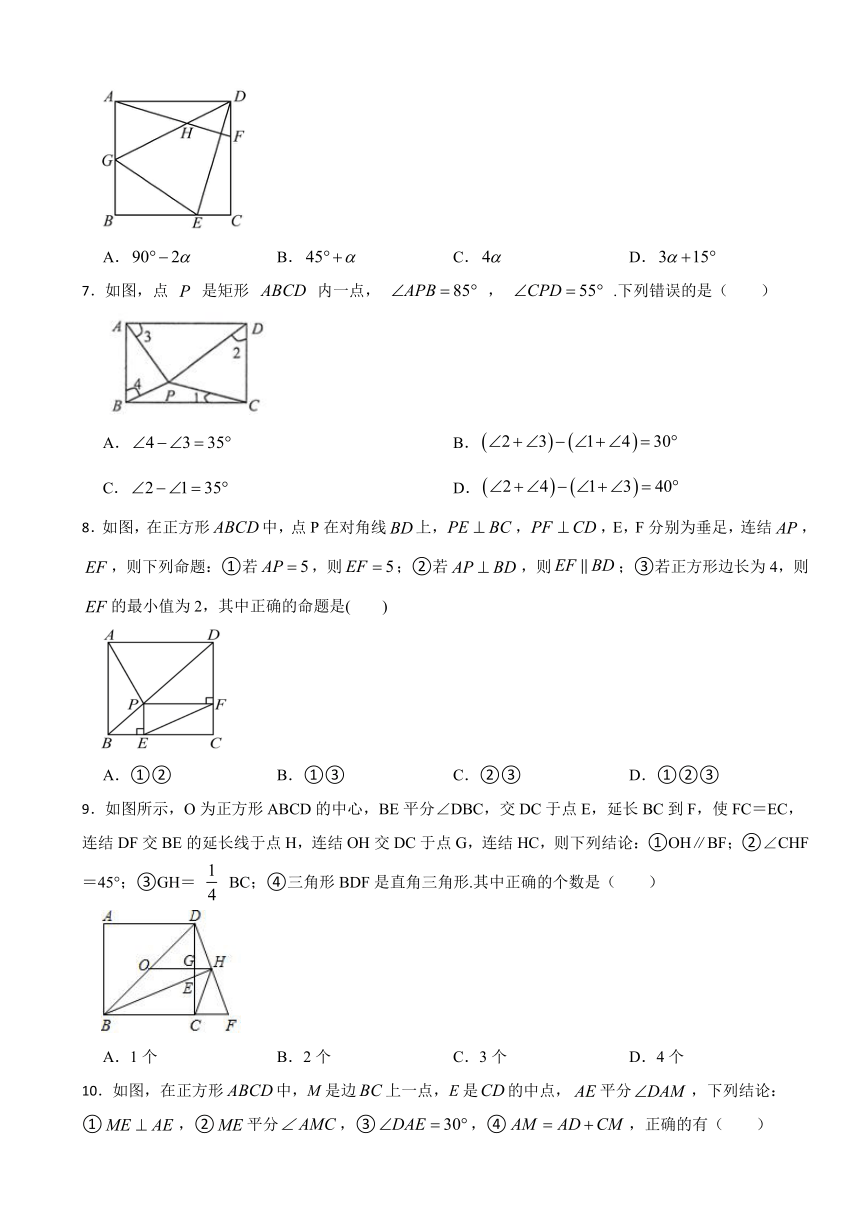
6.如图,在正方形中,点E、F分别在边上,满足,连接,点G在边上,连接交于点H,使得,连接,若,则的度数为( )
A. B. C. D.
7.如图,点 是矩形 内一点, , .下列错误的是( )
A. B.
C. D.
8.如图,在正方形中,点P在对角线上,,,E,F分别为垂足,连结,,则下列命题:①若,则;②若,则;③若正方形边长为4,则的最小值为2,其中正确的命题是( )
A.①② B.①③ C.②③ D.①②③
9.如图所示,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④三角形BDF是直角三角形.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,在正方形中,M是边上一点,E是的中点,平分,下列结论:①,②平分,③,④,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在矩形中,,连接,分别以点A和点C为圆心,大于一半的长为半径作圆弧,两弧相交于点M和点N,直线分别交于点E、F,连接.给出下面四个结论:①;②四边形是菱形;③;④.上述结论中,所有正确结论的序号是 .
12.如图,已知在四边形中,对角线,交于点O,且,要使四边形是矩形,可添加一个条件是 .
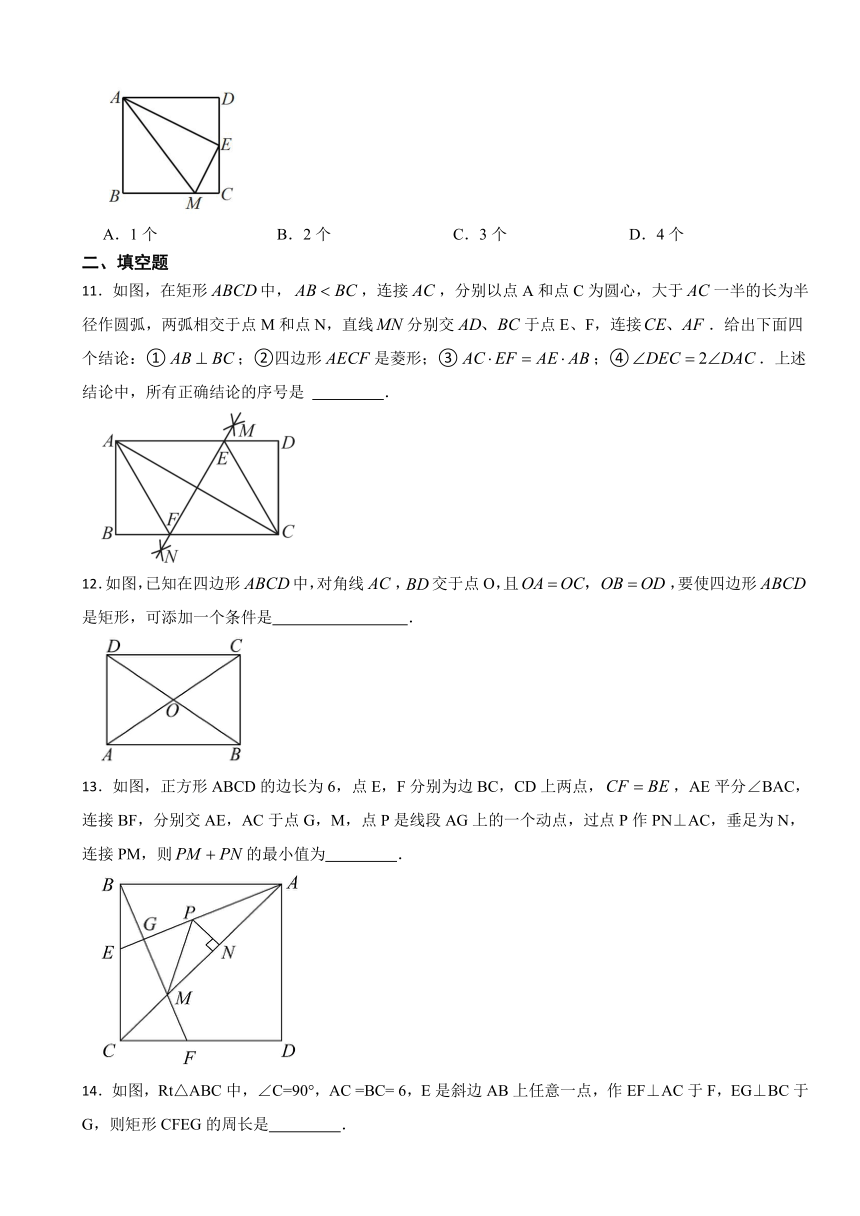
13.如图,正方形ABCD的边长为6,点E,F分别为边BC,CD上两点,,AE平分∠BAC,连接BF,分别交AE,AC于点G,M,点P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM,则的最小值为 .
14.如图,Rt△ABC中,∠C=90°,AC =BC= 6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则矩形CFEG的周长是 .
15.如图,在平面直角坐标系xOy中.四边形OABC为正方形,点A的坐标为.若直线:和直线:被正方形OABC的边所截得的线段长度相等,写山一组满足条件的与的值 .
16.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形中,,,则的长为 .
17.如图,在菱形ABCD中,∠C=60°,AB=2,延长BA至点E,使AE=1,现以点D为圆心,以DE的长为半径画弧,与直线BC相交于点M,则CM的长为 .
18.俊俊和霞霞共同合作将一张长为,宽为1的矩形纸片进行裁剪(共裁剪三次),裁剪出来的图形刚好是4个等腰三角形(无纸张剩余).霞霞说:“有一个等腰三角形的腰长是1”;俊俊说:“有一个等腰三角形的腰长是”;那么另外两个等腰三角形的腰长可能是 .
三、解答题
19.如图,菱形的对角线、相交于点,,,与交于点,,.
(1)求的长;
(2)求菱形的高.
20.如图,小亮将升旗的绳子拉到杆底端,绳子末刚好接触地面,然后将绳子末端拉到距离旗杆处,发现此时绳子末端距离地面.请你求出杆的高度(滑轮上方的高度忽略不计,解题时请在图中标注字母)
21.如图,在菱形中,对角线与相交于点,且,,求菱形的高的长度是多少?
22.如图,在△ABC中,D,E分别是边 AB,AC 的中点,且BE=2DE.延长 DE 至点 F,使得EF=BE,连结CF.
(1)求证:四边形 BCFE 是菱形.
(2)若 CE= 6,∠BEF =120°,求四边形BCFE的面积.
23.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在BD上,且AE∥CF,连接AF,CE.
(1)求证:四边形AECF是平行四边形;
(2)若∠EAO+∠CFD=180°,求证:四边形AECF是矩形.
24.如图,把矩形OABC放入平面直角坐标系xOy中,使分别落在x,y轴的正半轴上,其中,对角线AC所在直线解析式为,将矩形OABC沿着BE折叠,使点A落在边OC上的D处.
(1)求点B的坐标;
(2)求EA的长度;
(3)点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,如不存在,请说明理由.
25.在平面直角坐标系中,已知O为坐标原点,点 ,以点A为旋转中心,把顺时针旋转,得.
(Ⅰ)如图①,当旋转后满足 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 上的一点P旋转后的对应点为 ,当 取得最小值时,求点P的坐标(直接写出结果即可)
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】①②④
12.【答案】不唯一
13.【答案】
14.【答案】12
15.【答案】b1=1,b2=5(答案不唯一)
16.【答案】
17.【答案】1或3
18.【答案】1或或
19.【答案】(1)
(2)
20.【答案】
21.【答案】
22.【答案】(1)证明:∵ 在△ABC中,D,E分别是边 AB,AC 的中点,
∴DE∥BC,DE=BC,
又∵ BE=2DE,
∴BE=BC,
∵EF=BE,
∴BC=EF,
∴四边形BCFE是平行四边形,
而BE=BC,
∴四边形BCFE是菱形;
(2)解:由(1)得:DE∥BC,
∴∠BEF+∠EBC=180°,
∵ ∠BEF =120°,
∴∠EBC=60°,
由(1)得:BE=BC,
∴△BCE是等边三角形,
∵CE=6,
∴BC=BE=6,
过E作ET⊥BC于T,
∴∠BET=30°,
∴BT=3,
∴ET=,
∴S菱形BCFE=BC×ET=6×3=18.
23.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC.
∵AE∥CF,
∴∠EAO=∠FCO.
∵∠AOE=∠COF,
∴△AEO≌△CFO(ASA),
∴OE=OF,
∴四边形AECF是平行四边形.
(2)证明:∵∠EAO+∠CFD=180°,
∠CFO+∠CFD=180°,
∴∠EAO=∠CFO.
∵∠EAO=∠FCO,
∴∠FCO=∠CFO,
∴OC=OF,
由(1)可知四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∴AC=EF,
∴平行四边形AECF是矩形.
24.【答案】(1)B(6,10)
(2)
(3)
25.【答案】A解:(Ⅰ)如图①中,作 轴于H.
∵ ,
∴ ,
∴四边形 是矩形,
∴ ,
∴ ,
∴
(Ⅱ)如图②中,作 于K.
在 中,∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
,
∴直线A′D的解析式为 ,
点P坐标
一、单选题
1.两条对角线互相垂直平分的四边形是( )
A.等腰梯形 B.菱形 C.矩形 D.平行四边形
2.如图,平行四边形ABCD的对角线AC,BD相交于点O,添加下列条件仍不能判断四边形ABCD是菱形的是( )
A.AB=AD B.AO2+BO2=AB2
C.AC=BD D.∠BAC=∠ACB
3.如图,为庆祝“五·一”劳动节,某单位要在广场上布置一个矩形的花坛美化环境,计划用红花摆成两条对角线.如果一条对角线用了51盆红花,则另一条对角线还需要红花盆数是( )
A.49盆 B.50盆 C.51盆 D.52盆
4.菱形中,对角线长度分别为6和8,则菱形的面积是( )
A.24 B.12 C.36 D.10
5.如图,正方形的边长为8,点M在上,且,N是上一动点,则的最小值为( ).
A.8 B. C. D.10
6.如图,在正方形中,点E、F分别在边上,满足,连接,点G在边上,连接交于点H,使得,连接,若,则的度数为( )
A. B. C. D.
7.如图,点 是矩形 内一点, , .下列错误的是( )
A. B.
C. D.
8.如图,在正方形中,点P在对角线上,,,E,F分别为垂足,连结,,则下列命题:①若,则;②若,则;③若正方形边长为4,则的最小值为2,其中正确的命题是( )
A.①② B.①③ C.②③ D.①②③
9.如图所示,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④三角形BDF是直角三角形.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,在正方形中,M是边上一点,E是的中点,平分,下列结论:①,②平分,③,④,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在矩形中,,连接,分别以点A和点C为圆心,大于一半的长为半径作圆弧,两弧相交于点M和点N,直线分别交于点E、F,连接.给出下面四个结论:①;②四边形是菱形;③;④.上述结论中,所有正确结论的序号是 .
12.如图,已知在四边形中,对角线,交于点O,且,要使四边形是矩形,可添加一个条件是 .
13.如图,正方形ABCD的边长为6,点E,F分别为边BC,CD上两点,,AE平分∠BAC,连接BF,分别交AE,AC于点G,M,点P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM,则的最小值为 .
14.如图,Rt△ABC中,∠C=90°,AC =BC= 6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则矩形CFEG的周长是 .
15.如图,在平面直角坐标系xOy中.四边形OABC为正方形,点A的坐标为.若直线:和直线:被正方形OABC的边所截得的线段长度相等,写山一组满足条件的与的值 .
16.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形中,,,则的长为 .
17.如图,在菱形ABCD中,∠C=60°,AB=2,延长BA至点E,使AE=1,现以点D为圆心,以DE的长为半径画弧,与直线BC相交于点M,则CM的长为 .
18.俊俊和霞霞共同合作将一张长为,宽为1的矩形纸片进行裁剪(共裁剪三次),裁剪出来的图形刚好是4个等腰三角形(无纸张剩余).霞霞说:“有一个等腰三角形的腰长是1”;俊俊说:“有一个等腰三角形的腰长是”;那么另外两个等腰三角形的腰长可能是 .
三、解答题
19.如图,菱形的对角线、相交于点,,,与交于点,,.
(1)求的长;
(2)求菱形的高.
20.如图,小亮将升旗的绳子拉到杆底端,绳子末刚好接触地面,然后将绳子末端拉到距离旗杆处,发现此时绳子末端距离地面.请你求出杆的高度(滑轮上方的高度忽略不计,解题时请在图中标注字母)
21.如图,在菱形中,对角线与相交于点,且,,求菱形的高的长度是多少?
22.如图,在△ABC中,D,E分别是边 AB,AC 的中点,且BE=2DE.延长 DE 至点 F,使得EF=BE,连结CF.
(1)求证:四边形 BCFE 是菱形.
(2)若 CE= 6,∠BEF =120°,求四边形BCFE的面积.
23.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在BD上,且AE∥CF,连接AF,CE.
(1)求证:四边形AECF是平行四边形;
(2)若∠EAO+∠CFD=180°,求证:四边形AECF是矩形.
24.如图,把矩形OABC放入平面直角坐标系xOy中,使分别落在x,y轴的正半轴上,其中,对角线AC所在直线解析式为,将矩形OABC沿着BE折叠,使点A落在边OC上的D处.
(1)求点B的坐标;
(2)求EA的长度;
(3)点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,如不存在,请说明理由.
25.在平面直角坐标系中,已知O为坐标原点,点 ,以点A为旋转中心,把顺时针旋转,得.
(Ⅰ)如图①,当旋转后满足 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 上的一点P旋转后的对应点为 ,当 取得最小值时,求点P的坐标(直接写出结果即可)
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】①②④
12.【答案】不唯一
13.【答案】
14.【答案】12
15.【答案】b1=1,b2=5(答案不唯一)
16.【答案】
17.【答案】1或3
18.【答案】1或或
19.【答案】(1)
(2)
20.【答案】
21.【答案】
22.【答案】(1)证明:∵ 在△ABC中,D,E分别是边 AB,AC 的中点,
∴DE∥BC,DE=BC,
又∵ BE=2DE,
∴BE=BC,
∵EF=BE,
∴BC=EF,
∴四边形BCFE是平行四边形,
而BE=BC,
∴四边形BCFE是菱形;
(2)解:由(1)得:DE∥BC,
∴∠BEF+∠EBC=180°,
∵ ∠BEF =120°,
∴∠EBC=60°,
由(1)得:BE=BC,
∴△BCE是等边三角形,
∵CE=6,
∴BC=BE=6,
过E作ET⊥BC于T,
∴∠BET=30°,
∴BT=3,
∴ET=,
∴S菱形BCFE=BC×ET=6×3=18.
23.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC.
∵AE∥CF,
∴∠EAO=∠FCO.
∵∠AOE=∠COF,
∴△AEO≌△CFO(ASA),
∴OE=OF,
∴四边形AECF是平行四边形.
(2)证明:∵∠EAO+∠CFD=180°,
∠CFO+∠CFD=180°,
∴∠EAO=∠CFO.
∵∠EAO=∠FCO,
∴∠FCO=∠CFO,
∴OC=OF,
由(1)可知四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∴AC=EF,
∴平行四边形AECF是矩形.
24.【答案】(1)B(6,10)
(2)
(3)
25.【答案】A解:(Ⅰ)如图①中,作 轴于H.
∵ ,
∴ ,
∴四边形 是矩形,
∴ ,
∴ ,
∴
(Ⅱ)如图②中,作 于K.
在 中,∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
,
∴直线A′D的解析式为 ,
点P坐标
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
