优课沪科版初中数学七年级下8.2整式乘法之多项式与多项式相乘课件(共11张PPT)
文档属性
| 名称 | 优课沪科版初中数学七年级下8.2整式乘法之多项式与多项式相乘课件(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 543.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-24 00:00:00 | ||
图片预览




文档简介
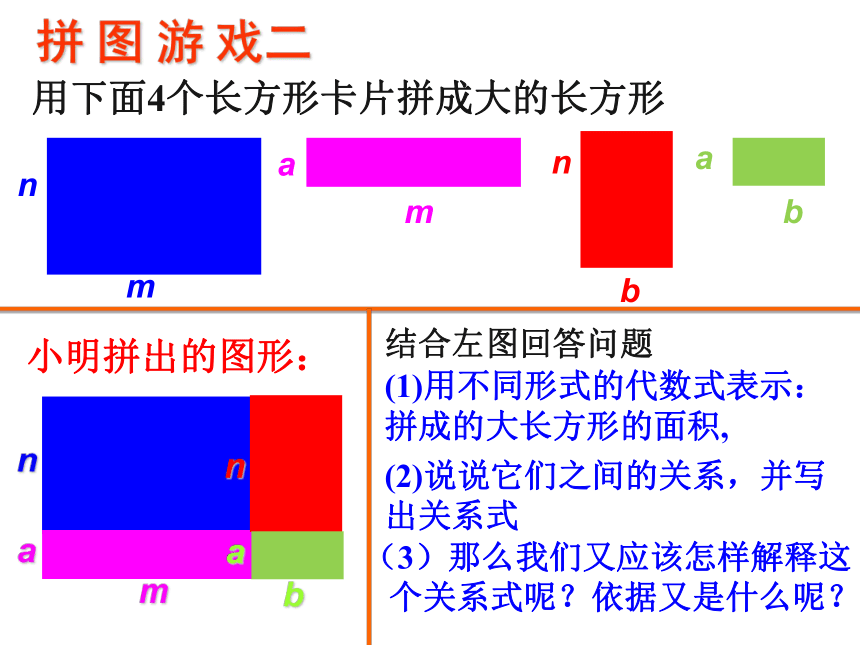
课件11张PPT。 多项式与多项式相乘(1)用不同形式的代数式表示:拼成的大长方形的面积, 小明拼出的图形 用下面2个长方形卡片拼成一个大 的长方形, 结合左图回答问题(2)说说它们之间的关系,并写出关系式(3)从单项式乘以多项式的运算
法则解释这个关系式,依据是什
么?拼 图 游 戏一拼 图 游 戏二小明拼出的图形:(1)用不同形式的代数式表示: 拼成的大长方形的面积, (2)说说它们之间的关系,并写
出关系式(3)那么我们又应该怎样解释这
个关系式呢?依据又是什么呢?用下面4个长方形卡片拼成大的长方形结合左图回答问题(1)用不同的形式表示所拼图的面积(m+b)(n+a)m(n+a)+b(n+a)mn+ma+bn+ba==①(m+b)(n+a)②m(n+a)+b(n+a)④mn+ma+bn+ba③n(m+b)+a (m+b)(2)说说上述几个代数式之间的关系,写出关系式(m+b)(n+a)=n(m+b)+a(m+b)mn+bn+ma+ba= 你能用乘法分配律 ,解释下列等式是怎样成 立的吗?(m+b)(n+a)=m(n+a) + b(n+a)可得:=mn+ma+bn+bamn+ ma+ ma+ bn+ bn 我们可以把 (n+a) 看成单项式, 把(m+b)看成多项式,运用单项式乘多项式的法则,(m+b)(n+a)m(n+a)+b(n+a)mn+ma+bn+ba== 根据上述运算规律?总结多项式与多项式相乘的运算法则? 先用一个多项式的每一项去乘另一个多项
式的每一项,再把所得的积相加。mn+ ma+ bn+ bn例题解析 【例】计算: (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x同号得正
异号得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2.最后的结果要合并同类项. 随堂练习(1)(m+2n)(m?2n); (2)(2n +5)(n?3) ; 计算:(3)(ax+b)(cx+d ) .思 考:如何计算下列各式。(1) (3a-2b)2提示:(1) (a+b)n= (a+b). . .n个 (a+b) 相 乘本节课你的收获是什么?1,多项式乘以多项式的 依据是什么?2,如何进行多项式与多项式乘法运算?3,运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄合并同类项 随堂练习 计算:(3) (3x+1)(x-2) (4 )(x+2y)2 (1)(2-3x)(2+3x) (2) (x-8y)(x-y)
法则解释这个关系式,依据是什
么?拼 图 游 戏一拼 图 游 戏二小明拼出的图形:(1)用不同形式的代数式表示: 拼成的大长方形的面积, (2)说说它们之间的关系,并写
出关系式(3)那么我们又应该怎样解释这
个关系式呢?依据又是什么呢?用下面4个长方形卡片拼成大的长方形结合左图回答问题(1)用不同的形式表示所拼图的面积(m+b)(n+a)m(n+a)+b(n+a)mn+ma+bn+ba==①(m+b)(n+a)②m(n+a)+b(n+a)④mn+ma+bn+ba③n(m+b)+a (m+b)(2)说说上述几个代数式之间的关系,写出关系式(m+b)(n+a)=n(m+b)+a(m+b)mn+bn+ma+ba= 你能用乘法分配律 ,解释下列等式是怎样成 立的吗?(m+b)(n+a)=m(n+a) + b(n+a)可得:=mn+ma+bn+bamn+ ma+ ma+ bn+ bn 我们可以把 (n+a) 看成单项式, 把(m+b)看成多项式,运用单项式乘多项式的法则,(m+b)(n+a)m(n+a)+b(n+a)mn+ma+bn+ba== 根据上述运算规律?总结多项式与多项式相乘的运算法则? 先用一个多项式的每一项去乘另一个多项
式的每一项,再把所得的积相加。mn+ ma+ bn+ bn例题解析 【例】计算: (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x同号得正
异号得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2.最后的结果要合并同类项. 随堂练习(1)(m+2n)(m?2n); (2)(2n +5)(n?3) ; 计算:(3)(ax+b)(cx+d ) .思 考:如何计算下列各式。(1) (3a-2b)2提示:(1) (a+b)n= (a+b). . .n个 (a+b) 相 乘本节课你的收获是什么?1,多项式乘以多项式的 依据是什么?2,如何进行多项式与多项式乘法运算?3,运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄合并同类项 随堂练习 计算:(3) (3x+1)(x-2) (4 )(x+2y)2 (1)(2-3x)(2+3x) (2) (x-8y)(x-y)
