3.2 一元一次方程及其解法 第2课时 课时作业(含答案)2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 3.2 一元一次方程及其解法 第2课时 课时作业(含答案)2024-2025学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 33.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 00:00:00 | ||
图片预览

文档简介
3.2 一元一次方程及其解法 第2课时
【基础达标】
1.解方程-1=,去分母时方程两边都乘 ( )
A.10 B.12 C.24 D.6
2.将-=5变形为x-x=50-,其错误的原因是 ( )
A.不应将分子分母同时扩大10倍
B.违背等式性质
C.移项未改变符号
D.去括号出现符号错误
3.方程-1=去分母得 .
4.当代数式x-的值等于1时,x的值是 .
5.将方程-=3的分母化为整数,方程变为 .
6.解方程:(1)x-=2-;
(2)=.
7.若整式与的差为1,求x的值.
【能力巩固】
8.要使代数式6+与的值相等,x的值为 ( )
A. B.- C. D.-
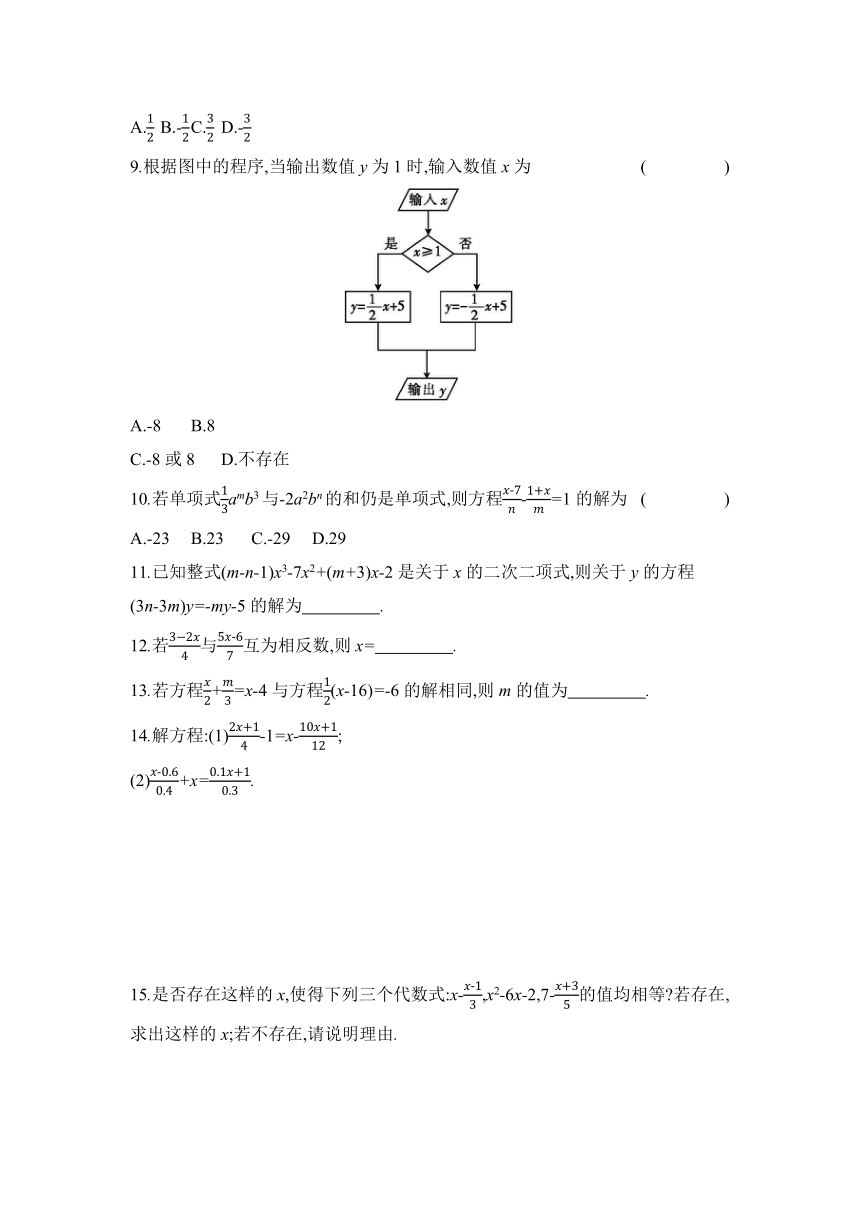
9.根据图中的程序,当输出数值y为1时,输入数值x为 ( )
A.-8 B.8
C.-8或8 D.不存在
10.若单项式amb3与-2a2bn的和仍是单项式,则方程-=1的解为 ( )
A.-23 B.23 C.-29 D.29
11.已知整式(m-n-1)x3-7x2+(m+3)x-2是关于x的二次二项式,则关于y的方程(3n-3m)y=-my-5的解为 .
12.若与互为相反数,则x= .
13.若方程+=x-4与方程(x-16)=-6的解相同,则m的值为 .
14.解方程:(1)-1=x-;
(2)+x=.
15.是否存在这样的x,使得下列三个代数式:x-,x2-6x-2,7-的值均相等 若存在,求出这样的x;若不存在,请说明理由.
【素养拓展】
16.当x取何值时,代数式2(3x+4)的值比5(2x-7)的值大3
17.某同学在对方程=-1去分母时,方程右边的-1没有乘3,因而求得方程的解为x=2,试求a的值,并正确地解方程.
18.用 表示一种运算,它的含义是:A B=+.如果2 1=,请计算出3 4的值.
参考答案
【基础达标】
1.B 2.B 3.5x-10=2x 4.1
5.5(x-2)-2(x+1)=3
6.解:(1)6x-3(x-1)=12-2(x+2),
6x-3x+3=12-2x-4,6x-3x+2x=12-4-3,
5x=5,x=1.
(2)4(2x-1)=3(5x+1),8x-4=15x+3,
8x-15x=3+4,-7x=7,x=-1.
7.解:由题意得-=1,
去分母,得2(2x+1)-(5x-1)=6,
去括号,得4x+2-5x+1=6,
移项,得4x-5x=6-2-1,
合并同类项,得-x=3,
系数化为1,得x=-3.
【能力巩固】
8.D 9.D 10.A 11.y= 12. 13.-6
14.解:(1)3(2x+1)-12=12x-(10x+1),
6x+3-12=12x-10x-1,
6x-12x+10x=-3+12-1,
4x=8,x=2.
(2)原方程化为+x=,
3(5x-3)+6x=2(x+10),
15x-9+6x=2x+20,
19x=29,x=.
15.解:假设存在这样的x,则x-=7-,
去分母,得15x-5x+5=105-3x-9,解得x=7.
将x=7分别代入,得x-=7-=5;
x2-6x-2=72-6×7-2=5;
7-=7-=5.
上述代数式的值均为5,
则存在这样的x=7.
答:存在,x等于7.
【素养拓展】
16.解:由题意,得2(3x+4)-5(2x-7)=3,解得x=10.
即当x=10时,代数式2(3x+4)的值比5(2x-7)的值大3.
17.解:根据题意,x=2是方程2x-1=x+a-1的根,
所以2×2-1=2+a-1,解得a=2,
所以原方程为=-1,
去分母,得2x-1=x+2-3,
移项,合并同类项,得x=0.
18.解:化简2 1=,得+=,
去分母,得2+x=10,
解得x=8,
则3 4=+=.
【基础达标】
1.解方程-1=,去分母时方程两边都乘 ( )
A.10 B.12 C.24 D.6
2.将-=5变形为x-x=50-,其错误的原因是 ( )
A.不应将分子分母同时扩大10倍
B.违背等式性质
C.移项未改变符号
D.去括号出现符号错误
3.方程-1=去分母得 .
4.当代数式x-的值等于1时,x的值是 .
5.将方程-=3的分母化为整数,方程变为 .
6.解方程:(1)x-=2-;
(2)=.
7.若整式与的差为1,求x的值.
【能力巩固】
8.要使代数式6+与的值相等,x的值为 ( )
A. B.- C. D.-
9.根据图中的程序,当输出数值y为1时,输入数值x为 ( )
A.-8 B.8
C.-8或8 D.不存在
10.若单项式amb3与-2a2bn的和仍是单项式,则方程-=1的解为 ( )
A.-23 B.23 C.-29 D.29
11.已知整式(m-n-1)x3-7x2+(m+3)x-2是关于x的二次二项式,则关于y的方程(3n-3m)y=-my-5的解为 .
12.若与互为相反数,则x= .
13.若方程+=x-4与方程(x-16)=-6的解相同,则m的值为 .
14.解方程:(1)-1=x-;
(2)+x=.
15.是否存在这样的x,使得下列三个代数式:x-,x2-6x-2,7-的值均相等 若存在,求出这样的x;若不存在,请说明理由.
【素养拓展】
16.当x取何值时,代数式2(3x+4)的值比5(2x-7)的值大3
17.某同学在对方程=-1去分母时,方程右边的-1没有乘3,因而求得方程的解为x=2,试求a的值,并正确地解方程.
18.用 表示一种运算,它的含义是:A B=+.如果2 1=,请计算出3 4的值.
参考答案
【基础达标】
1.B 2.B 3.5x-10=2x 4.1
5.5(x-2)-2(x+1)=3
6.解:(1)6x-3(x-1)=12-2(x+2),
6x-3x+3=12-2x-4,6x-3x+2x=12-4-3,
5x=5,x=1.
(2)4(2x-1)=3(5x+1),8x-4=15x+3,
8x-15x=3+4,-7x=7,x=-1.
7.解:由题意得-=1,
去分母,得2(2x+1)-(5x-1)=6,
去括号,得4x+2-5x+1=6,
移项,得4x-5x=6-2-1,
合并同类项,得-x=3,
系数化为1,得x=-3.
【能力巩固】
8.D 9.D 10.A 11.y= 12. 13.-6
14.解:(1)3(2x+1)-12=12x-(10x+1),
6x+3-12=12x-10x-1,
6x-12x+10x=-3+12-1,
4x=8,x=2.
(2)原方程化为+x=,
3(5x-3)+6x=2(x+10),
15x-9+6x=2x+20,
19x=29,x=.
15.解:假设存在这样的x,则x-=7-,
去分母,得15x-5x+5=105-3x-9,解得x=7.
将x=7分别代入,得x-=7-=5;
x2-6x-2=72-6×7-2=5;
7-=7-=5.
上述代数式的值均为5,
则存在这样的x=7.
答:存在,x等于7.
【素养拓展】
16.解:由题意,得2(3x+4)-5(2x-7)=3,解得x=10.
即当x=10时,代数式2(3x+4)的值比5(2x-7)的值大3.
17.解:根据题意,x=2是方程2x-1=x+a-1的根,
所以2×2-1=2+a-1,解得a=2,
所以原方程为=-1,
去分母,得2x-1=x+2-3,
移项,合并同类项,得x=0.
18.解:化简2 1=,得+=,
去分母,得2+x=10,
解得x=8,
则3 4=+=.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
