3.5 二元一次方程组的应用 第2课时 课时作业(含答案)2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 3.5 二元一次方程组的应用 第2课时 课时作业(含答案)2024-2025学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 34.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 00:00:00 | ||
图片预览

文档简介
3.5 二元一次方程组的应用 第2课时
【基础达标】
1.端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师购买荷包x个,五彩绳y个,根据题意,下面列出的方程组正确的是 ( )
A. B.
C. D.
2.某个体商店在一次买卖中同时卖出两件上衣,每件都是以135元卖出,若按成本计算,其中一件盈利25%,另一件亏损25%,则这家商店在这次买卖中 ( )
A.不赔不赚 B.赚9元
C.赔8元 D.赔18元
3.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长为 ( )
A.25尺 B.20尺
C.15尺 D.10尺
4.花蕊小朋友用280元买了每支0.2元的铅笔和每支5元的钢笔,一共200支,寄给偏远山区的小朋友,则她买了 支铅笔, 支钢笔.
5.《歌词古体算题》中有“巧算笔砚”题:
甲借乙家七砚,还他三管毛锥,贴钱四百又八十,恰好齐同了毕.
丙却借乙九笔,还他三个端溪,一百八十贴乙齐,二色价该各几
这题意思就是:甲向乙家借了7个砚台,除还给他3支上等毛笔外,另补给他480文钱,刚好等价.丙向乙家借了9支毛笔,除还给他3个端溪砚台外,另补给他180文钱,恰好等价.试问笔、砚各价值多少
【能力巩固】
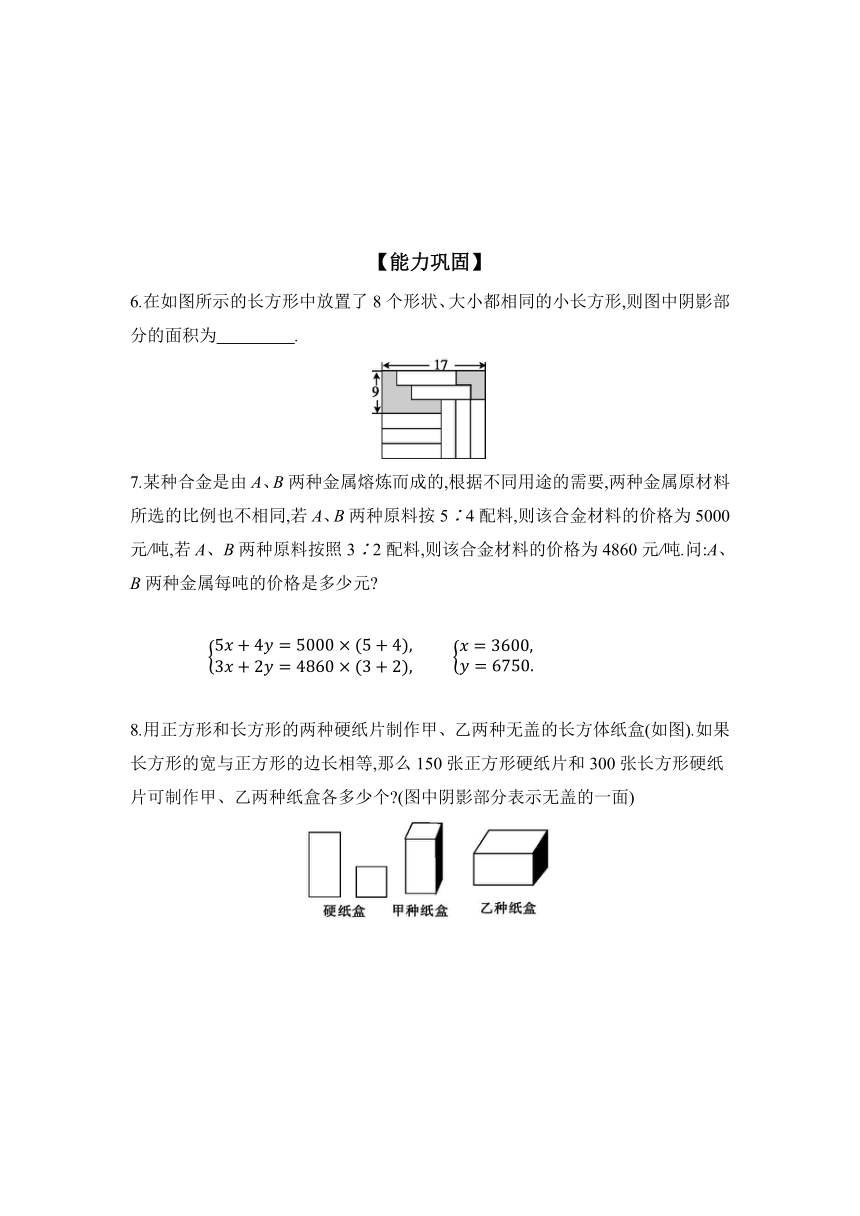
6.在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
7.某种合金是由A、B两种金属熔炼而成的,根据不同用途的需要,两种金属原材料所选的比例也不相同,若A、B两种原料按5∶4配料,则该合金材料的价格为5000元/吨,若A、B两种原料按照3∶2配料,则该合金材料的价格为4860元/吨.问:A、B两种金属每吨的价格是多少元
8.用正方形和长方形的两种硬纸片制作甲、乙两种无盖的长方体纸盒(如图).如果长方形的宽与正方形的边长相等,那么150张正方形硬纸片和300张长方形硬纸片可制作甲、乙两种纸盒各多少个 (图中阴影部分表示无盖的一面)
9.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,问甲、乙两件服装的成本各是多少元
【素养拓展】
10.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种电视机每台1500元,乙种每台2100元,丙种每台2500元.若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案.
参考答案
【基础达标】
1.B 2.D 3.B 4.150 50
5.解:如果设砚台价为x文,笔价y文,由题意,得方程组
解得
即砚价90文,笔价50文.
【能力巩固】
6.79
7.解:设A种金属每吨的价格为x元,B种金属每吨的价格为y元,
依题意得解得
答:A种金属每吨的价格为3600元,B种金属每吨的价格为6750元.
8.解:设可制作甲种纸盒x个,乙种纸盒y个,根据题意,得
解这个方程组,得
答:可制作甲种纸盒60个,乙种纸盒30个.
9.解:设甲服装的成本是x元,乙服装的成本是y元.
依题意,得
解得
答:甲、乙两件服装的成本分别为300元、200元.
【素养拓展】
10.解:设甲、乙、丙型号的电视机分别为x台、y台、z台.
(1)若选甲、乙,
则有
解得
(2)若选甲、丙,
则有
解得
(3)若选乙、丙,
则有
解得(不符合题意,舍去).
答:有两种进货方案:(1)购进甲种电视机25台,乙种25台;(2)购进甲种电视机35台,丙种15台.
【基础达标】
1.端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师购买荷包x个,五彩绳y个,根据题意,下面列出的方程组正确的是 ( )
A. B.
C. D.
2.某个体商店在一次买卖中同时卖出两件上衣,每件都是以135元卖出,若按成本计算,其中一件盈利25%,另一件亏损25%,则这家商店在这次买卖中 ( )
A.不赔不赚 B.赚9元
C.赔8元 D.赔18元
3.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长为 ( )
A.25尺 B.20尺
C.15尺 D.10尺
4.花蕊小朋友用280元买了每支0.2元的铅笔和每支5元的钢笔,一共200支,寄给偏远山区的小朋友,则她买了 支铅笔, 支钢笔.
5.《歌词古体算题》中有“巧算笔砚”题:
甲借乙家七砚,还他三管毛锥,贴钱四百又八十,恰好齐同了毕.
丙却借乙九笔,还他三个端溪,一百八十贴乙齐,二色价该各几
这题意思就是:甲向乙家借了7个砚台,除还给他3支上等毛笔外,另补给他480文钱,刚好等价.丙向乙家借了9支毛笔,除还给他3个端溪砚台外,另补给他180文钱,恰好等价.试问笔、砚各价值多少
【能力巩固】
6.在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
7.某种合金是由A、B两种金属熔炼而成的,根据不同用途的需要,两种金属原材料所选的比例也不相同,若A、B两种原料按5∶4配料,则该合金材料的价格为5000元/吨,若A、B两种原料按照3∶2配料,则该合金材料的价格为4860元/吨.问:A、B两种金属每吨的价格是多少元
8.用正方形和长方形的两种硬纸片制作甲、乙两种无盖的长方体纸盒(如图).如果长方形的宽与正方形的边长相等,那么150张正方形硬纸片和300张长方形硬纸片可制作甲、乙两种纸盒各多少个 (图中阴影部分表示无盖的一面)
9.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,问甲、乙两件服装的成本各是多少元
【素养拓展】
10.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种电视机每台1500元,乙种每台2100元,丙种每台2500元.若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案.
参考答案
【基础达标】
1.B 2.D 3.B 4.150 50
5.解:如果设砚台价为x文,笔价y文,由题意,得方程组
解得
即砚价90文,笔价50文.
【能力巩固】
6.79
7.解:设A种金属每吨的价格为x元,B种金属每吨的价格为y元,
依题意得解得
答:A种金属每吨的价格为3600元,B种金属每吨的价格为6750元.
8.解:设可制作甲种纸盒x个,乙种纸盒y个,根据题意,得
解这个方程组,得
答:可制作甲种纸盒60个,乙种纸盒30个.
9.解:设甲服装的成本是x元,乙服装的成本是y元.
依题意,得
解得
答:甲、乙两件服装的成本分别为300元、200元.
【素养拓展】
10.解:设甲、乙、丙型号的电视机分别为x台、y台、z台.
(1)若选甲、乙,
则有
解得
(2)若选甲、丙,
则有
解得
(3)若选乙、丙,
则有
解得(不符合题意,舍去).
答:有两种进货方案:(1)购进甲种电视机25台,乙种25台;(2)购进甲种电视机35台,丙种15台.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
