4.2 线段、射线、直线 课时作业(含答案)2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 4.2 线段、射线、直线 课时作业(含答案)2024-2025学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 105.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 00:00:00 | ||
图片预览

文档简介
4.2 线段、射线、直线
【基础达标】
1.延长线段AB到点C,下列说法中正确的是 ( )
A.点C在线段AB上
B.点C在直线AB上
C.点C不在直线AB上
D.点C在直线AB的延长线上
2.下列说法正确的是 ( )
A.射线PA和射线AP是同一条射线
B.射线OA的长度是12 cm
C.直线ab、cd相交于点M
D.两点确定一条直线
3.下列各图中,表示“射线CD”的是 ( )
A B
C D
4.如图,能用字母表示的直线有 条,它们是 ;能用字母表示的线段有 条,它们是 ;在直线EF上能用字母表示的射线有 条,它们是 .
5.木匠师傅在木料上画线,先确定两个点的位置就能把线画得很直,这样做的依据是 .
6.如图,A,B,C,D是圆周上的4个点,连接其中任意两点可得到一条线段,这样的线段共可连出 条.
7.经过A、B、C三点可连接直线的条数为 .
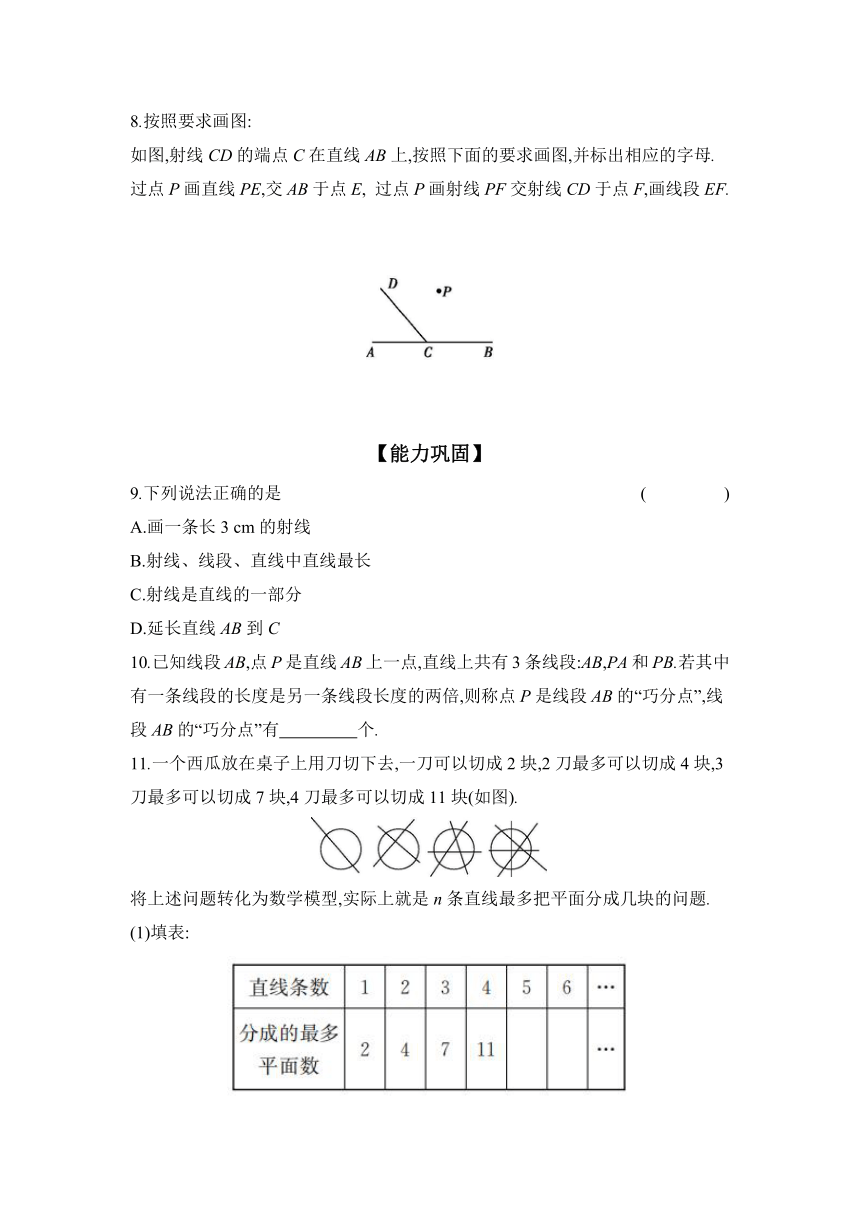
8.按照要求画图:
如图,射线CD的端点C在直线AB上,按照下面的要求画图,并标出相应的字母.
过点P画直线PE,交AB于点E, 过点P画射线PF交射线CD于点F,画线段EF.
【能力巩固】
9.下列说法正确的是 ( )
A.画一条长3 cm的射线
B.射线、线段、直线中直线最长
C.射线是直线的一部分
D.延长直线AB到C
10.已知线段AB,点P是直线AB上一点,直线上共有3条线段:AB,PA和PB.若其中有一条线段的长度是另一条线段长度的两倍,则称点P是线段AB的“巧分点”,线段AB的“巧分点”有 个.
11.一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块,3刀最多可以切成7块,4刀最多可以切成11块(如图).
将上述问题转化为数学模型,实际上就是n条直线最多把平面分成几块的问题.
(1)填表:
(2)n条直线把平面最多分成的块数是 .(不需要解题过程)
【素养拓展】
12.通过阅读所得的启示来回答问题(阅读中的结论可直接用).
阅读:若在直线上有n个不同的点,则此直线上共有多少条线段
分析:通过画图尝试,得表格如下.
问题:
(1)在直线上有n个不同的点,则此图中共有多少条线段
(2)某学校七年级共有8个班进行辩论赛,规定进行单循环赛(每两班之间赛一场),那么七年级的辩论赛共有多少场次
(3)有一辆客车,往返两地,中途停靠三个车站,问有多少种不同的票价 要准备多少种车票
参考答案
【基础达标】
1.B 2.D 3.B
4.3 直线AD、直线AB、直线BD 6 线段AB、线段AC、线段AD、线段BC、线段CD、线段BD 6 射线BE、射线BF、射线CE、射线CF、射线DE、射线DF
5.两点确定一条直线
6.6
7.一条或三条
8.解:如图所示:
【能力巩固】
9.C 10.9
11.解:(1)16;22.
提示:5条直线时,分成的最多平面数是1+1+2+3+4+5=16;
6条直线时,分成的最多平面数是1+1+2+3+4+5+6=22.
(2)1+1+2+3+…+n或1+.
【素养拓展】
12.解:(1)在直线上有n个不同的点,则此图中共有条线段.
(2)当n=8时,比赛场次==28.
(3)5个站点共有=10种不同的票价,每两站之间要准备往返两种车票,所以需要准备20种不同的车票.
【基础达标】
1.延长线段AB到点C,下列说法中正确的是 ( )
A.点C在线段AB上
B.点C在直线AB上
C.点C不在直线AB上
D.点C在直线AB的延长线上
2.下列说法正确的是 ( )
A.射线PA和射线AP是同一条射线
B.射线OA的长度是12 cm
C.直线ab、cd相交于点M
D.两点确定一条直线
3.下列各图中,表示“射线CD”的是 ( )
A B
C D
4.如图,能用字母表示的直线有 条,它们是 ;能用字母表示的线段有 条,它们是 ;在直线EF上能用字母表示的射线有 条,它们是 .
5.木匠师傅在木料上画线,先确定两个点的位置就能把线画得很直,这样做的依据是 .
6.如图,A,B,C,D是圆周上的4个点,连接其中任意两点可得到一条线段,这样的线段共可连出 条.
7.经过A、B、C三点可连接直线的条数为 .
8.按照要求画图:
如图,射线CD的端点C在直线AB上,按照下面的要求画图,并标出相应的字母.
过点P画直线PE,交AB于点E, 过点P画射线PF交射线CD于点F,画线段EF.
【能力巩固】
9.下列说法正确的是 ( )
A.画一条长3 cm的射线
B.射线、线段、直线中直线最长
C.射线是直线的一部分
D.延长直线AB到C
10.已知线段AB,点P是直线AB上一点,直线上共有3条线段:AB,PA和PB.若其中有一条线段的长度是另一条线段长度的两倍,则称点P是线段AB的“巧分点”,线段AB的“巧分点”有 个.
11.一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块,3刀最多可以切成7块,4刀最多可以切成11块(如图).
将上述问题转化为数学模型,实际上就是n条直线最多把平面分成几块的问题.
(1)填表:
(2)n条直线把平面最多分成的块数是 .(不需要解题过程)
【素养拓展】
12.通过阅读所得的启示来回答问题(阅读中的结论可直接用).
阅读:若在直线上有n个不同的点,则此直线上共有多少条线段
分析:通过画图尝试,得表格如下.
问题:
(1)在直线上有n个不同的点,则此图中共有多少条线段
(2)某学校七年级共有8个班进行辩论赛,规定进行单循环赛(每两班之间赛一场),那么七年级的辩论赛共有多少场次
(3)有一辆客车,往返两地,中途停靠三个车站,问有多少种不同的票价 要准备多少种车票
参考答案
【基础达标】
1.B 2.D 3.B
4.3 直线AD、直线AB、直线BD 6 线段AB、线段AC、线段AD、线段BC、线段CD、线段BD 6 射线BE、射线BF、射线CE、射线CF、射线DE、射线DF
5.两点确定一条直线
6.6
7.一条或三条
8.解:如图所示:
【能力巩固】
9.C 10.9
11.解:(1)16;22.
提示:5条直线时,分成的最多平面数是1+1+2+3+4+5=16;
6条直线时,分成的最多平面数是1+1+2+3+4+5+6=22.
(2)1+1+2+3+…+n或1+.
【素养拓展】
12.解:(1)在直线上有n个不同的点,则此图中共有条线段.
(2)当n=8时,比赛场次==28.
(3)5个站点共有=10种不同的票价,每两站之间要准备往返两种车票,所以需要准备20种不同的车票.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
