人教A版(2019)数学选择必修1 3.1.2 椭圆的简单几何性质(第1课时)课件(26页ppt)
文档属性
| 名称 | 人教A版(2019)数学选择必修1 3.1.2 椭圆的简单几何性质(第1课时)课件(26页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 10:59:09 | ||
图片预览








文档简介
(共26张PPT)
选择必修
第三章 圆锥曲线的方程
3.1 椭圆
3.1.2 椭圆的简单几何性质(第1课时)
教学目标
学习目标 数学素养
1.掌握椭圆的范围、对称性、顶点、离心率等几何性质. 1.数学抽象素养和逻辑推理素养.
2.利用椭圆的简单几何性质求标准方程. 2.数学运算素养和逻辑推理素养.
3.能运用椭圆的简单几何性质分析和解决问题. 3.数学运算素养和直观想象素养.
温故知新
1.椭圆定义
把平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫做椭圆(ellipse). 这两个定点F1, F2叫做椭圆的焦点(foocus),两焦点之间的距离| F1F2|叫做椭圆的焦距(foocus distance) . 焦距的一半称为半焦距.
几何表示:|MF1|+|MF2|=2a(常数且2a>|F1F2|).
2.椭圆的标准方程
椭圆焦点在x轴上
(a>b>0).
椭圆焦点在y轴上
(a>b>0).
a2=b2+c2.
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质,包括椭圆的范围、形状、大小、对称性和特殊点等.
下面,我们用椭圆方程(a>b>0)来研究椭圆的性质.
通过对曲线的对称性以及特殊点的讨论,可以从整体上把握曲线的形状、大小和位置.所以,本章对几种圆锥曲线都是从范围、对称性、顶点及其他特性等方面研究它们的几何性质.
知新探究
观察椭圆(a>b>0)的形状, 你能从图上看出它的范围吗 它具有怎样的对称性 椭圆上哪些点比较特殊
1.范围
观察下图,容易看出椭圆上的点都在一个特殊的矩形内,你能利用方程(代数方法)确定出它的具体边界吗?
F1
F2
O
x
y
A1
A2
B1
B2
由方程(a>b>0),可知
,
∴,
即-a≤x≤a.
同理有-b≤y≤b.
这说明椭圆位于直线围成的矩形框里.
知新探究
在椭圆的标准方程 (a>b>0) 中,以-y代y ,方程不变.这说明当点P(x,y)在椭圆上时 ,它关于x轴的对称点(x,-y)也在椭圆上 ,所以椭圆关于x轴对称.
这时,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心.
综上,椭圆关于x轴、y轴都是对称的.
同理,以-x代x ,方程也不变.这说明当点P(x,y)在椭圆上时 ,它关于y轴的对称点(-x,y)也在椭圆上 ,所以椭圆关于y轴对称.
2.对称性
观察椭圆的形状 ,可以发现椭圆即是轴对称图形,又是中心对称图形,如何利用方程说明椭圆的对称性?
F1
F2
O
x
y
A1
A2
B1
B2
知新探究
因为x轴、y轴是椭圆的对称轴 ,所以椭圆与它的对称轴有四个交点, 这四个交点叫做椭圆的顶点(如图).
线段A1A2, B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2a, 2b. a和b分别叫做椭圆的长半轴长和短半轴长.
研究曲线上某些特殊点的位置,可以确定曲线的位置.
在椭圆的标准方程(a>b>0)中,令x=0,得.因此B1(0,-b),B2(0,b)是椭圆与y轴的两个交点.同理,令y=0,得.因此A1(-a,0),A2(a,0)是椭圆与x轴的两个交点.
你认为椭圆(a>b>0)上哪些点比较特殊?为什么?如何得到这些点的坐标?
3.顶点
知新探究
如右图,椭圆(a>b>0)的长半轴长为a ,半焦距为c. 通过几何画板演示发现,保持长半轴长a不变 ,改变椭圆的半焦距c,可以发现, c越接近a,椭圆越扁平.类似地, 保持c不变, 改变a的大小,则a越接近c,椭圆越扁平;而当a, c扩大或缩小相同倍数时,椭圆的形状不变.
观察右图,我们发现,不同椭圆的扁平程度不同. 扁平
程度是椭圆的重要形状特征,你能用适当的量定量刻画椭
圆的扁平程度吗
这样,利用c和a这两个量, 可以刻画椭圆的扁平程度.
4.离心率
我们把椭圆的焦距与长轴长的比 称为椭圆的离心率.用e表示,即 e= .
知新探究
因为a>c>1,所以0.
e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆;
e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就越扁;
我们把椭圆的焦距与长轴长的比 称为椭圆的离心率.用e表示,即 e= .
离心率越小,椭圆越圆,离心率越大,椭圆越扁.
你能运用函数知识解释,为什么越大,椭圆越扁平吗?越小,椭圆越接近于圆吗?
当且仅当a=b时,c=0,这时两个焦点重合,图形变为圆,它的方程为.
知新探究
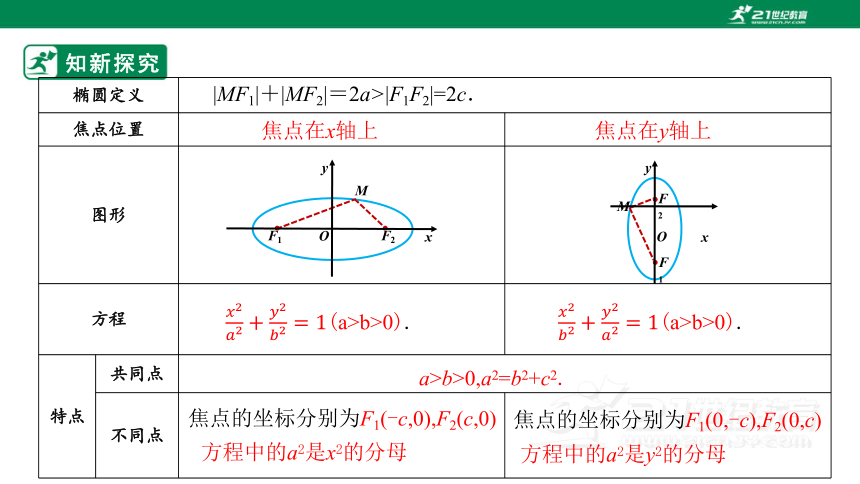
椭圆定义 焦点位置
图形
方程
特点 共同点 不同点
|MF1|+|MF2|=2a>|F1F2|=2c.
焦点在x轴上
F1
F2
M
x
y
O
(a>b>0).
焦点在y轴上
F1
F2
M
x
y
O
(a>b>0).
a>b>0,a2=b2+c2.
焦点的坐标分别为F1(-c,0),F2(c,0)
方程中的a2是x2的分母
焦点的坐标分别为F1(0,-c),F2(0,c)
方程中的a2是y2的分母
知新探究
焦点的位置 焦点在x轴上 焦点在y轴上
范围 _____________________ _____________________
对称性 对称轴为 ,对称中心为 . 顶点
轴长 短轴长|B1B2|=___,长轴长|A1A2|=___ 焦点 ____________________ _____________________
焦距 |F1F2|= ,c2= . 离心率 e= , e的范围是 . A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
-a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
2b
2a
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
x轴、y轴
(0,0)
2c
a2-b2
.
0知新探究
【例1】求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标..
解:
把原方程化成标准方程,得
因此,椭圆的长轴和短轴的长分别是2a=10和2b=8,离心率e=,两个焦点坐标分别是F1(-3,0)和F2(3,0),四个顶点坐标分别是A1(-5,0),A2(5,0),B1(0,-4)和B2(0,4).
.
于是a=5,b=4,c==3.
初试身手
1.已知椭圆C1:=1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
⑴求椭圆C1的长轴长、短轴长、焦点坐标及离心率;
解:
⑴由椭圆C1:=1,可得
∴椭圆C1的长轴长为20,短轴长为16.
∴椭圆C1的焦点坐标为(-6,0),(6,0),离心率为.
a=10,b=8
c==6,.
初试身手
1.已知椭圆C1:设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
⑵写出椭圆C2的方程,并研究其范围、对称性、顶点、焦点、焦距、离心率.
解:
①椭圆C2的范围:-8≤x≤8,-10≤y≤10;
③椭圆C2的顶点:长轴端点为(0,10),(0,-10),短轴端点为(-8,0),(8,0);
⑵椭圆C2:=1.①
②椭圆C2的对称性:对称轴:x轴、y轴;对称中心:(0,0);
④椭圆C2的焦点:(0,6),(0,-6),焦距为12;
⑤椭圆C2的离心率e=.
知新探究
【例2】求适合下列条件的椭圆的标准方程.
⑴短轴长2,离心率e=;
⑵在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
解:
⑴由题意,得 ,
∴,
解得,
∴所求椭圆的标准方程为.
知新探究
【例2】求适合下列条件的椭圆的标准方程.
⑴短轴长2,离心率e=;
⑵在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
解:
⑵由题意可设椭圆的方程为(a>b>0),
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),且|OF|=c,|A1A2|=2b,
∴所求椭圆的标准方程为.
∴c=b=3,a2=b2+c2=18.
初试身手
2.⑴已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线交椭圆于A,B两点,且|AB|=3,则C的标准方程为( )
A.+y2=1 B.=1 C.=1 D.=1
⑴由题意,设椭圆的方程为=1(a>b>0),可得c==1,
联立①②,可得a2=4,b2=3,
∴a2-b2=1,①
∵AB经过右焦点F2且垂直于x轴,且|AB|=3,
∴可得A,B,
∴椭圆的方程为为.故选C.
代入椭圆方程,得 =1,②
解:
C
初试身手
2.⑵已知椭圆C过点(3,0),且离心率为,则椭圆C的标准方程为( )
A.=1 B.=1或1
C.=1 D.=1或+=1
⑵若焦点在x轴上,则a=3.
此时椭圆C的标准方程为=1.
若焦点在y轴上,则b=3.
由e=,得c=,所以b2=a2-c2=3,
此时椭圆C的标准方程为=1.
故选D.
由e=,得a2=27,
解:
D
知新探究
【例3】⑴已知椭圆(a>b>0)的左焦点为F1(-c,0),A(-a,0),B(0,b)是两个顶点, 如果F1到直线AB的距离为, 求椭圆的离心率e.
解:
⑴由已知条件可得,直线AB的方程为,即bx-ay+ab=0,
又F1(-c,0),由点到直线距离公式可得,
化简整理,得8c2-14ac+5a2=0,
即8e2-14e+5=0,
方程两边同除以a2,得
,
解得,
∴椭圆的离心率.
知新探究
【例3】⑵(2022·全国甲卷)椭圆C:=1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为,则C的离心率为( )
A. B. C. D.
解:
⑵已知A(-a,0),设P(x0,y0),则Q(-x0,y0),x0≠±a,
而kAP=,kAQ=,
∴, ①
∵=1,即,②
将②代入①整理得.
∴e=,
故选A.
A
初试身手
方法1:设点M的坐标是(x0,y0),则|x0|由消去y0,得.
3. 若椭圆(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
∵0≤x02由①得c2≥b2,即c2≥a2-c2,
解:
又0∴,
∴a2≤2c2,即,
综上,椭圆的离心率e的取值范围是.
∴.
由②得c2-b2.
初试身手
方法2:设椭圆与y轴的一个交点为P,连接PF1,PF2.
∵椭圆上存在一点M,使∠F1MF2=90°,
3. 若椭圆(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
∴∠F1PF2≥90°,则c≥b,
∴c2≥b2=a2-c2,即a2≤2c2,,
解:
又0综上,椭圆的离心率e的取值范围是.
∴.
.
课堂小结
椭圆的几何性质
范围
对称性
顶点
离心率
方程的性质
椭圆的几何性质
研究圆锥曲线几何性质的一般思路与方法
作业布置
作业:
P115 习题3.1 第3,2,4⑶,5,10题.
补充:(选做)
1.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为
( )
A. B. C. D.
2.已知椭圆的焦距不小于短轴长,则椭圆的离心率的取值范围为________.
3.已知椭圆(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在一点P,使,则该椭圆的离心率的取值范围为____________.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修
第三章 圆锥曲线的方程
3.1 椭圆
3.1.2 椭圆的简单几何性质(第1课时)
教学目标
学习目标 数学素养
1.掌握椭圆的范围、对称性、顶点、离心率等几何性质. 1.数学抽象素养和逻辑推理素养.
2.利用椭圆的简单几何性质求标准方程. 2.数学运算素养和逻辑推理素养.
3.能运用椭圆的简单几何性质分析和解决问题. 3.数学运算素养和直观想象素养.
温故知新
1.椭圆定义
把平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫做椭圆(ellipse). 这两个定点F1, F2叫做椭圆的焦点(foocus),两焦点之间的距离| F1F2|叫做椭圆的焦距(foocus distance) . 焦距的一半称为半焦距.
几何表示:|MF1|+|MF2|=2a(常数且2a>|F1F2|).
2.椭圆的标准方程
椭圆焦点在x轴上
(a>b>0).
椭圆焦点在y轴上
(a>b>0).
a2=b2+c2.
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质,包括椭圆的范围、形状、大小、对称性和特殊点等.
下面,我们用椭圆方程(a>b>0)来研究椭圆的性质.
通过对曲线的对称性以及特殊点的讨论,可以从整体上把握曲线的形状、大小和位置.所以,本章对几种圆锥曲线都是从范围、对称性、顶点及其他特性等方面研究它们的几何性质.
知新探究
观察椭圆(a>b>0)的形状, 你能从图上看出它的范围吗 它具有怎样的对称性 椭圆上哪些点比较特殊
1.范围
观察下图,容易看出椭圆上的点都在一个特殊的矩形内,你能利用方程(代数方法)确定出它的具体边界吗?
F1
F2
O
x
y
A1
A2
B1
B2
由方程(a>b>0),可知
,
∴,
即-a≤x≤a.
同理有-b≤y≤b.
这说明椭圆位于直线围成的矩形框里.
知新探究
在椭圆的标准方程 (a>b>0) 中,以-y代y ,方程不变.这说明当点P(x,y)在椭圆上时 ,它关于x轴的对称点(x,-y)也在椭圆上 ,所以椭圆关于x轴对称.
这时,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心.
综上,椭圆关于x轴、y轴都是对称的.
同理,以-x代x ,方程也不变.这说明当点P(x,y)在椭圆上时 ,它关于y轴的对称点(-x,y)也在椭圆上 ,所以椭圆关于y轴对称.
2.对称性
观察椭圆的形状 ,可以发现椭圆即是轴对称图形,又是中心对称图形,如何利用方程说明椭圆的对称性?
F1
F2
O
x
y
A1
A2
B1
B2
知新探究
因为x轴、y轴是椭圆的对称轴 ,所以椭圆与它的对称轴有四个交点, 这四个交点叫做椭圆的顶点(如图).
线段A1A2, B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2a, 2b. a和b分别叫做椭圆的长半轴长和短半轴长.
研究曲线上某些特殊点的位置,可以确定曲线的位置.
在椭圆的标准方程(a>b>0)中,令x=0,得.因此B1(0,-b),B2(0,b)是椭圆与y轴的两个交点.同理,令y=0,得.因此A1(-a,0),A2(a,0)是椭圆与x轴的两个交点.
你认为椭圆(a>b>0)上哪些点比较特殊?为什么?如何得到这些点的坐标?
3.顶点
知新探究
如右图,椭圆(a>b>0)的长半轴长为a ,半焦距为c. 通过几何画板演示发现,保持长半轴长a不变 ,改变椭圆的半焦距c,可以发现, c越接近a,椭圆越扁平.类似地, 保持c不变, 改变a的大小,则a越接近c,椭圆越扁平;而当a, c扩大或缩小相同倍数时,椭圆的形状不变.
观察右图,我们发现,不同椭圆的扁平程度不同. 扁平
程度是椭圆的重要形状特征,你能用适当的量定量刻画椭
圆的扁平程度吗
这样,利用c和a这两个量, 可以刻画椭圆的扁平程度.
4.离心率
我们把椭圆的焦距与长轴长的比 称为椭圆的离心率.用e表示,即 e= .
知新探究
因为a>c>1,所以0
e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆;
e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就越扁;
我们把椭圆的焦距与长轴长的比 称为椭圆的离心率.用e表示,即 e= .
离心率越小,椭圆越圆,离心率越大,椭圆越扁.
你能运用函数知识解释,为什么越大,椭圆越扁平吗?越小,椭圆越接近于圆吗?
当且仅当a=b时,c=0,这时两个焦点重合,图形变为圆,它的方程为.
知新探究
椭圆定义 焦点位置
图形
方程
特点 共同点 不同点
|MF1|+|MF2|=2a>|F1F2|=2c.
焦点在x轴上
F1
F2
M
x
y
O
(a>b>0).
焦点在y轴上
F1
F2
M
x
y
O
(a>b>0).
a>b>0,a2=b2+c2.
焦点的坐标分别为F1(-c,0),F2(c,0)
方程中的a2是x2的分母
焦点的坐标分别为F1(0,-c),F2(0,c)
方程中的a2是y2的分母
知新探究
焦点的位置 焦点在x轴上 焦点在y轴上
范围 _____________________ _____________________
对称性 对称轴为 ,对称中心为 . 顶点
轴长 短轴长|B1B2|=___,长轴长|A1A2|=___ 焦点 ____________________ _____________________
焦距 |F1F2|= ,c2= . 离心率 e= , e的范围是 . A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
-a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
2b
2a
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
x轴、y轴
(0,0)
2c
a2-b2
.
0
【例1】求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标..
解:
把原方程化成标准方程,得
因此,椭圆的长轴和短轴的长分别是2a=10和2b=8,离心率e=,两个焦点坐标分别是F1(-3,0)和F2(3,0),四个顶点坐标分别是A1(-5,0),A2(5,0),B1(0,-4)和B2(0,4).
.
于是a=5,b=4,c==3.
初试身手
1.已知椭圆C1:=1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
⑴求椭圆C1的长轴长、短轴长、焦点坐标及离心率;
解:
⑴由椭圆C1:=1,可得
∴椭圆C1的长轴长为20,短轴长为16.
∴椭圆C1的焦点坐标为(-6,0),(6,0),离心率为.
a=10,b=8
c==6,.
初试身手
1.已知椭圆C1:设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
⑵写出椭圆C2的方程,并研究其范围、对称性、顶点、焦点、焦距、离心率.
解:
①椭圆C2的范围:-8≤x≤8,-10≤y≤10;
③椭圆C2的顶点:长轴端点为(0,10),(0,-10),短轴端点为(-8,0),(8,0);
⑵椭圆C2:=1.①
②椭圆C2的对称性:对称轴:x轴、y轴;对称中心:(0,0);
④椭圆C2的焦点:(0,6),(0,-6),焦距为12;
⑤椭圆C2的离心率e=.
知新探究
【例2】求适合下列条件的椭圆的标准方程.
⑴短轴长2,离心率e=;
⑵在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
解:
⑴由题意,得 ,
∴,
解得,
∴所求椭圆的标准方程为.
知新探究
【例2】求适合下列条件的椭圆的标准方程.
⑴短轴长2,离心率e=;
⑵在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
解:
⑵由题意可设椭圆的方程为(a>b>0),
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),且|OF|=c,|A1A2|=2b,
∴所求椭圆的标准方程为.
∴c=b=3,a2=b2+c2=18.
初试身手
2.⑴已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线交椭圆于A,B两点,且|AB|=3,则C的标准方程为( )
A.+y2=1 B.=1 C.=1 D.=1
⑴由题意,设椭圆的方程为=1(a>b>0),可得c==1,
联立①②,可得a2=4,b2=3,
∴a2-b2=1,①
∵AB经过右焦点F2且垂直于x轴,且|AB|=3,
∴可得A,B,
∴椭圆的方程为为.故选C.
代入椭圆方程,得 =1,②
解:
C
初试身手
2.⑵已知椭圆C过点(3,0),且离心率为,则椭圆C的标准方程为( )
A.=1 B.=1或1
C.=1 D.=1或+=1
⑵若焦点在x轴上,则a=3.
此时椭圆C的标准方程为=1.
若焦点在y轴上,则b=3.
由e=,得c=,所以b2=a2-c2=3,
此时椭圆C的标准方程为=1.
故选D.
由e=,得a2=27,
解:
D
知新探究
【例3】⑴已知椭圆(a>b>0)的左焦点为F1(-c,0),A(-a,0),B(0,b)是两个顶点, 如果F1到直线AB的距离为, 求椭圆的离心率e.
解:
⑴由已知条件可得,直线AB的方程为,即bx-ay+ab=0,
又F1(-c,0),由点到直线距离公式可得,
化简整理,得8c2-14ac+5a2=0,
即8e2-14e+5=0,
方程两边同除以a2,得
,
解得,
∴椭圆的离心率.
知新探究
【例3】⑵(2022·全国甲卷)椭圆C:=1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为,则C的离心率为( )
A. B. C. D.
解:
⑵已知A(-a,0),设P(x0,y0),则Q(-x0,y0),x0≠±a,
而kAP=,kAQ=,
∴, ①
∵=1,即,②
将②代入①整理得.
∴e=,
故选A.
A
初试身手
方法1:设点M的坐标是(x0,y0),则|x0|
3. 若椭圆(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
∵0≤x02
解:
又0
∴a2≤2c2,即,
综上,椭圆的离心率e的取值范围是.
∴.
由②得c2-b2
初试身手
方法2:设椭圆与y轴的一个交点为P,连接PF1,PF2.
∵椭圆上存在一点M,使∠F1MF2=90°,
3. 若椭圆(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
∴∠F1PF2≥90°,则c≥b,
∴c2≥b2=a2-c2,即a2≤2c2,,
解:
又0
∴.
.
课堂小结
椭圆的几何性质
范围
对称性
顶点
离心率
方程的性质
椭圆的几何性质
研究圆锥曲线几何性质的一般思路与方法
作业布置
作业:
P115 习题3.1 第3,2,4⑶,5,10题.
补充:(选做)
1.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为
( )
A. B. C. D.
2.已知椭圆的焦距不小于短轴长,则椭圆的离心率的取值范围为________.
3.已知椭圆(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在一点P,使,则该椭圆的离心率的取值范围为____________.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
