6.3 特殊的平行四边形-矩形的判定教案
文档属性
| 名称 | 6.3 特殊的平行四边形-矩形的判定教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 65.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-24 09:21:06 | ||
图片预览

文档简介
安乐镇中学数学教案
编写时间:2016年 月 日 上课时间:2016年 月 日 总序第6个教案
课 题 特殊的平行四边形 主 备 人 汤广建 授课人
年 级 八年级 课 时 4 课 型 新授课
三 维 目 标 知识与能力 1.探索并掌握矩形的判定定理,会证明判定。2.掌握它们之间的区别与联系
过程与方法 在观察、操作的探索过程中,发展学生的合情推理能力.
情感、态度、价值观 通过探究活动,激发学习兴趣,体会转化思想,学会类比的研究方法。
教学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )重点 矩形的判定方法。
教学难点 合理应用矩形的判定定理解决问题。
教学方法 引导发现探究、讲和练相结合.
教 具
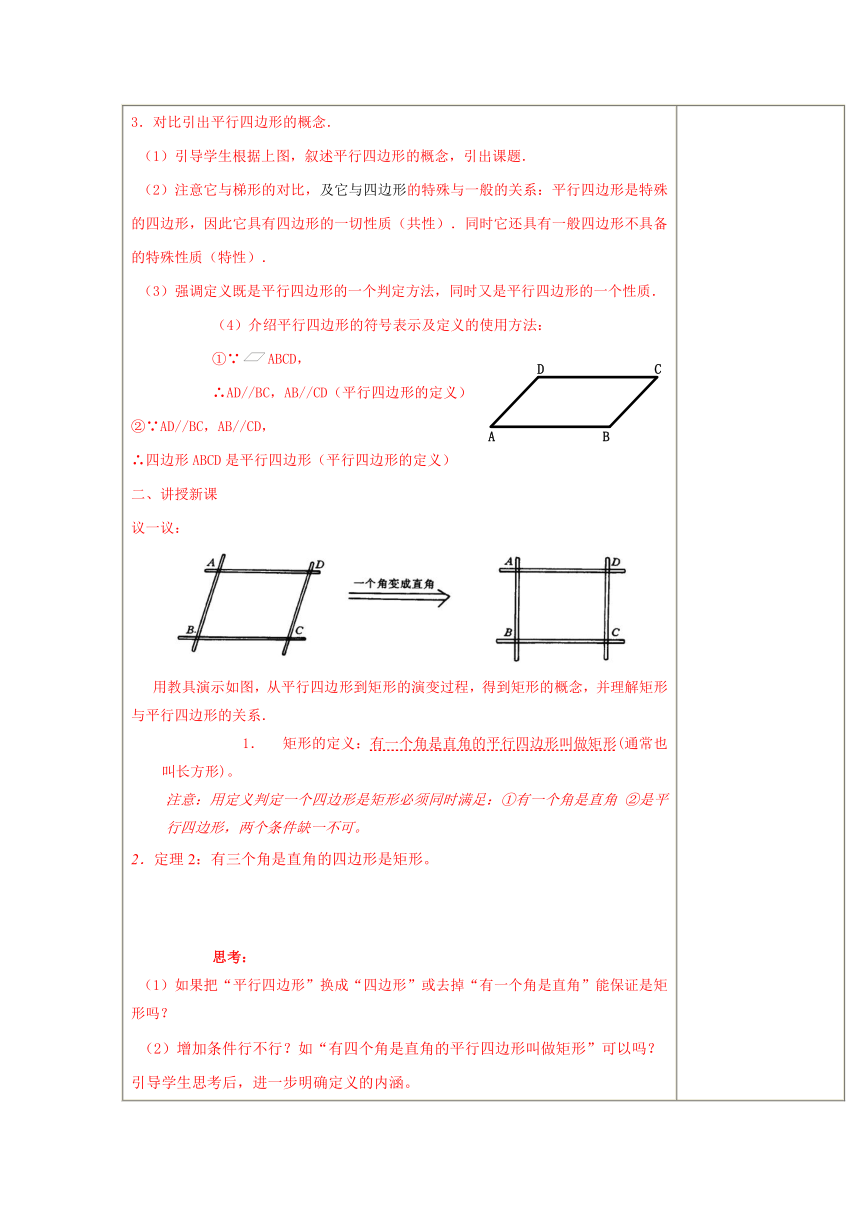
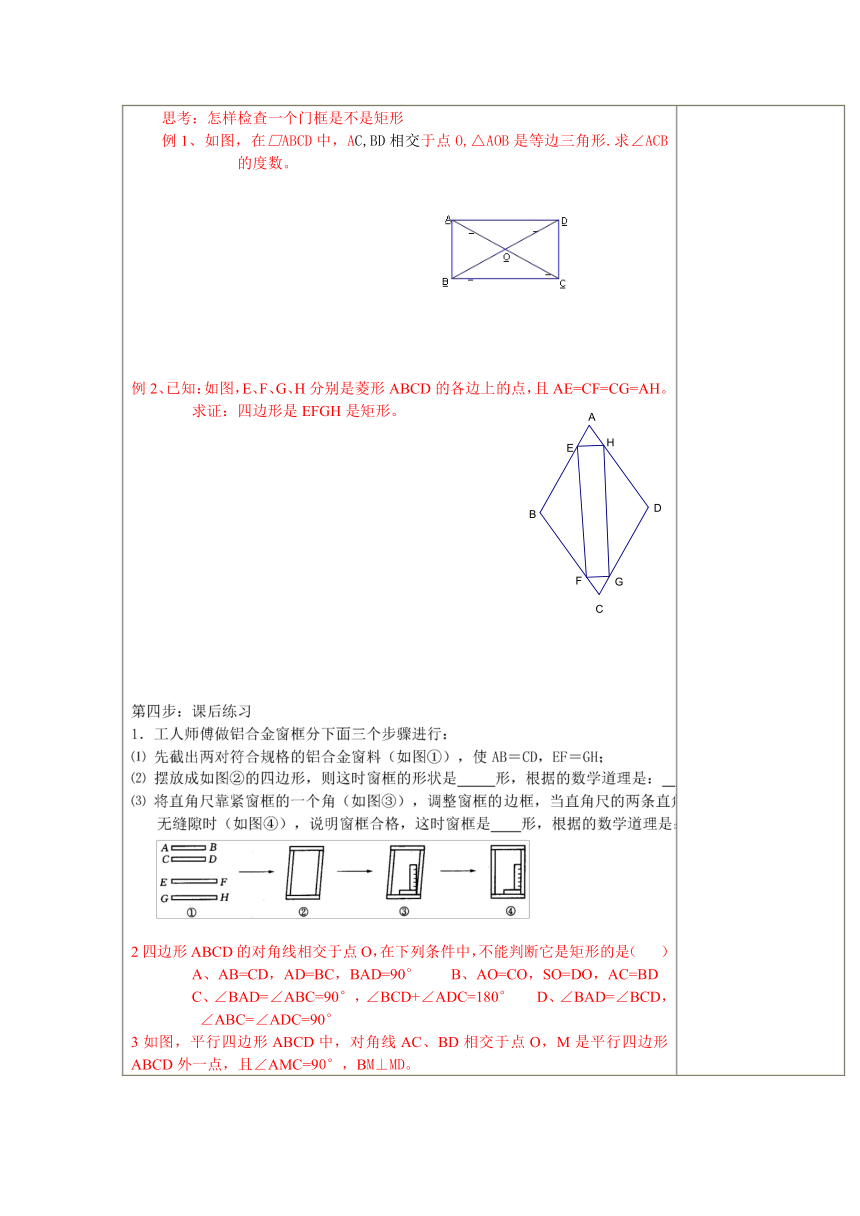
一、利用分类、特殊化的方法引出平行四边形的概念 1.复习四边形的知识. (1)引导学生画任意凸四边形,指出它的主要元素——顶点、边、角、对角线。强调对角线的作用:将四边形分割化归为三角形来研究.(2)将四边形的边角按位置关系分为两类:边 角教学时应结合图形,让学生识别清楚,并注意与三角形中角的对边、边的对角相区别.2.教师提问:四边形中的两组对边按位置关系分为几种情况?引导学生画图回答,并出示四边形与特殊四边形的关系,如图. ( http: / / www.21cnjy.com / )3.对比引出平行四边形的概念. (1)引导学生根据上图,叙述平行四边形的概念,引出课题. (2)注意它与梯形的对比,及它与四边形 ( http: / / www.21cnjy.com )的特殊与一般的关系:平行四边形是特殊的四边形,因此它具有四边形的一切性质(共性).同时它还具有一般四边形不具备的特殊性质(特性). (3)强调定义既是平行四边形的一个判定方法,同时又是平行四边形的一个性质.(4)介绍平行四边形的符号表示及定义的使用方法: ①∵ABCD,∴AD//BC,AB//CD(平行四边形的定义) ②∵AD//BC,AB//CD,∴四边形ABCD是平行四边形(平行四边形的定义)二、讲授新课议一议: ( http: / / www.21cnjy.com / )用教具演示如图,从平行四边形到矩形的演变过程,得到矩形的概念,并理解矩形与平行四边形的关系.矩形的定义:有一个角是直角的平行四边形叫做矩形(通常也叫长方形)。注意:用定义判定一个四边形是矩形必须同时满足:①有一个角是直角 ②是平行四边形,两个条件缺一不可。2.定理2:有三个角是直角的四边形是矩形。思考: (1)如果把“平行四边形”换成“四边形”或去掉“有一个角是直角”能保证是矩形吗? (2)增加条件行不行?如“有四个角是直角的平行四边形叫做矩形”可以吗?引导学生思考后,进一步明确定义的内涵。思考:怎样检查一个门框是不是矩形例1、如图,在□ABCD中,AC,BD相交 ( http: / / www.21cnjy.com )于点O,△AOB是等边三角形.求∠ACB的度数。 ( http: / / www.21cnjy.com / ) 例2、已知:如图,E、F、G、H分别是菱形ABCD的各边上的点,且AE=CF=CG=AH。求证:四边形是EFGH是矩形。 ( http: / / www.21cnjy.com / )2四边形ABCD的对角线相交于点O,在下列条件中,不能判断它是矩形的是( )A、AB=CD,AD=BC,BAD=90° B、AO=CO,SO=DO,AC=BDC、∠BAD=∠ABC=90°,∠BCD+∠ADC=180° D、∠BAD=∠BCD, ∠ABC=∠ADC=90°3如图,平行四边形ABCD中,对角线AC、BD相交于点O,M是平行四边形ABCD外一点,且∠AMC=90°,BM⊥MD。五课堂小结矩形的判定方法分两类:从四边形来判定和从平行四边形来判定.常用的判定方法有三种:定义和两个判定定理.遇到具体题目,可根据条件灵活选用当六布置作业P23 第2题 二次备课应改进的地方:
教学反思:
编写时间:2016年 月 日 上课时间:2016年 月 日 总序第6个教案
课 题 特殊的平行四边形 主 备 人 汤广建 授课人
年 级 八年级 课 时 4 课 型 新授课
三 维 目 标 知识与能力 1.探索并掌握矩形的判定定理,会证明判定。2.掌握它们之间的区别与联系
过程与方法 在观察、操作的探索过程中,发展学生的合情推理能力.
情感、态度、价值观 通过探究活动,激发学习兴趣,体会转化思想,学会类比的研究方法。
教学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )重点 矩形的判定方法。
教学难点 合理应用矩形的判定定理解决问题。
教学方法 引导发现探究、讲和练相结合.
教 具
一、利用分类、特殊化的方法引出平行四边形的概念 1.复习四边形的知识. (1)引导学生画任意凸四边形,指出它的主要元素——顶点、边、角、对角线。强调对角线的作用:将四边形分割化归为三角形来研究.(2)将四边形的边角按位置关系分为两类:边 角教学时应结合图形,让学生识别清楚,并注意与三角形中角的对边、边的对角相区别.2.教师提问:四边形中的两组对边按位置关系分为几种情况?引导学生画图回答,并出示四边形与特殊四边形的关系,如图. ( http: / / www.21cnjy.com / )3.对比引出平行四边形的概念. (1)引导学生根据上图,叙述平行四边形的概念,引出课题. (2)注意它与梯形的对比,及它与四边形 ( http: / / www.21cnjy.com )的特殊与一般的关系:平行四边形是特殊的四边形,因此它具有四边形的一切性质(共性).同时它还具有一般四边形不具备的特殊性质(特性). (3)强调定义既是平行四边形的一个判定方法,同时又是平行四边形的一个性质.(4)介绍平行四边形的符号表示及定义的使用方法: ①∵ABCD,∴AD//BC,AB//CD(平行四边形的定义) ②∵AD//BC,AB//CD,∴四边形ABCD是平行四边形(平行四边形的定义)二、讲授新课议一议: ( http: / / www.21cnjy.com / )用教具演示如图,从平行四边形到矩形的演变过程,得到矩形的概念,并理解矩形与平行四边形的关系.矩形的定义:有一个角是直角的平行四边形叫做矩形(通常也叫长方形)。注意:用定义判定一个四边形是矩形必须同时满足:①有一个角是直角 ②是平行四边形,两个条件缺一不可。2.定理2:有三个角是直角的四边形是矩形。思考: (1)如果把“平行四边形”换成“四边形”或去掉“有一个角是直角”能保证是矩形吗? (2)增加条件行不行?如“有四个角是直角的平行四边形叫做矩形”可以吗?引导学生思考后,进一步明确定义的内涵。思考:怎样检查一个门框是不是矩形例1、如图,在□ABCD中,AC,BD相交 ( http: / / www.21cnjy.com )于点O,△AOB是等边三角形.求∠ACB的度数。 ( http: / / www.21cnjy.com / ) 例2、已知:如图,E、F、G、H分别是菱形ABCD的各边上的点,且AE=CF=CG=AH。求证:四边形是EFGH是矩形。 ( http: / / www.21cnjy.com / )2四边形ABCD的对角线相交于点O,在下列条件中,不能判断它是矩形的是( )A、AB=CD,AD=BC,BAD=90° B、AO=CO,SO=DO,AC=BDC、∠BAD=∠ABC=90°,∠BCD+∠ADC=180° D、∠BAD=∠BCD, ∠ABC=∠ADC=90°3如图,平行四边形ABCD中,对角线AC、BD相交于点O,M是平行四边形ABCD外一点,且∠AMC=90°,BM⊥MD。五课堂小结矩形的判定方法分两类:从四边形来判定和从平行四边形来判定.常用的判定方法有三种:定义和两个判定定理.遇到具体题目,可根据条件灵活选用当六布置作业P23 第2题 二次备课应改进的地方:
教学反思:
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
