22.3 实际问题与二次函数 同步练习(含答案)2024-2025学年人教版九年级数学上册
文档属性
| 名称 | 22.3 实际问题与二次函数 同步练习(含答案)2024-2025学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 541.9KB | ||
| 资源类型 | 教案 | ||
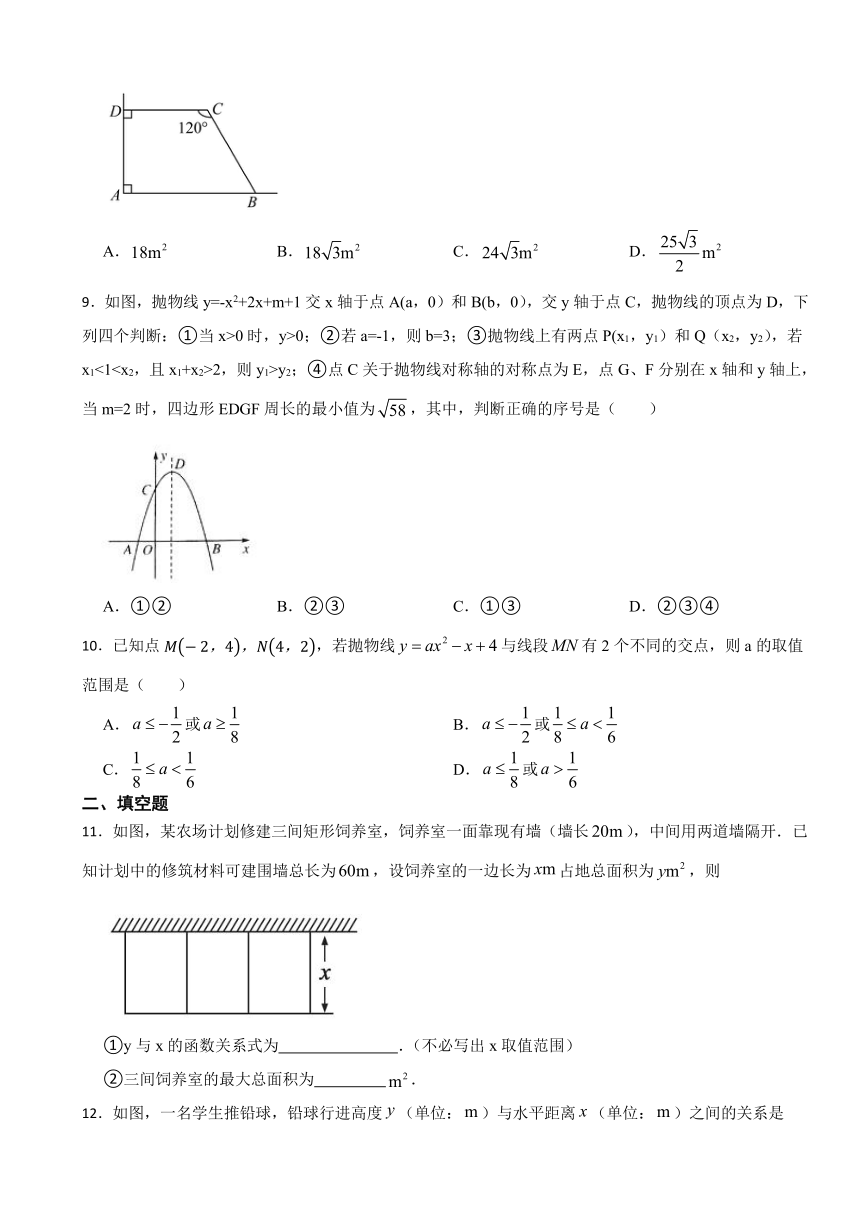
| 版本资源 | 人教版 | ||
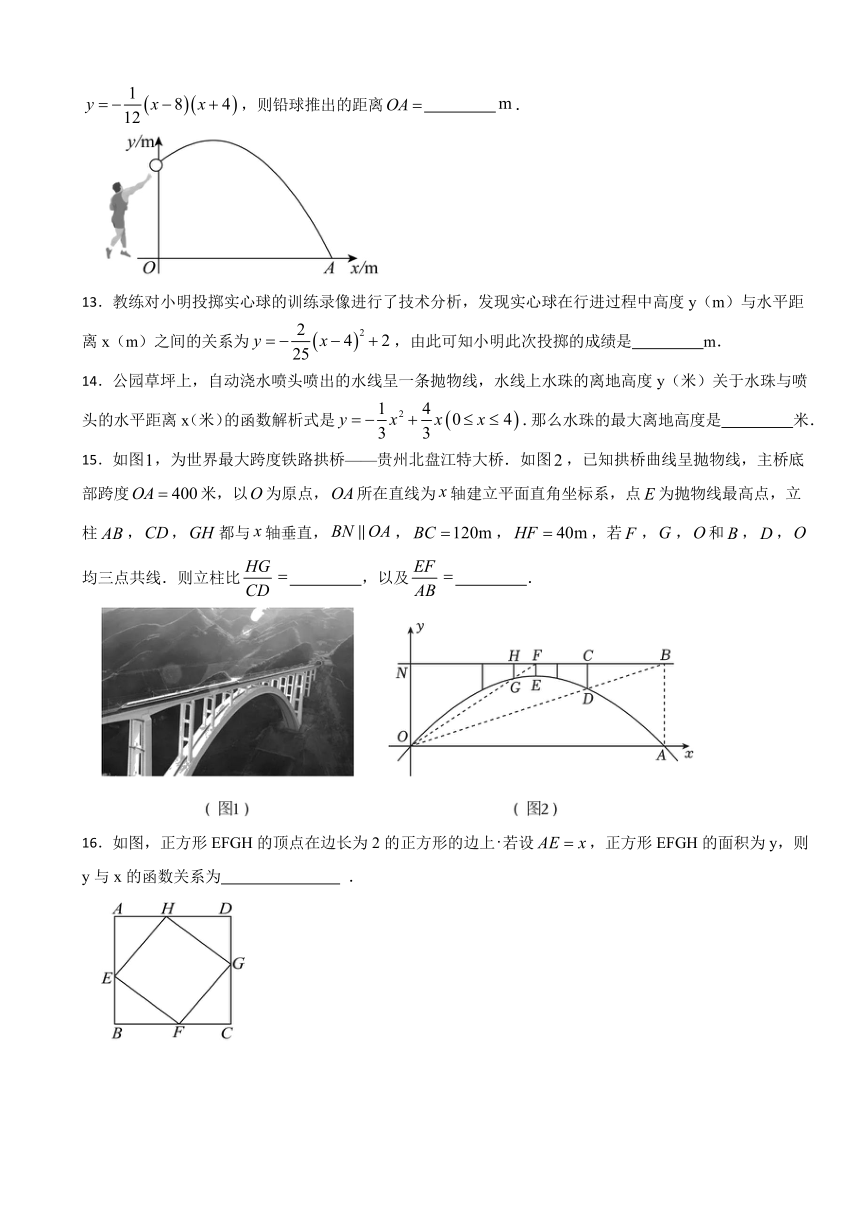
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 00:00:00 | ||
图片预览


文档简介
22.3 实际问题与二次函数 同步练习2024-2025学年人教版九年级数学上册
一、单选题
1.如图是抛物线型拱桥,当拱顶高离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m B.2m C.m D.m
2.某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
3.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系,下列对方程的两根与的解释正确的是( )
A.小球的飞行高度为15m时,小球飞行的时间是1s
B.小球飞行时飞行高度为15m,并将继续上升
C.小球从飞出到落地要用4s
D.小球的飞行高度可以达到25m
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t= ;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③ B.①②③ C.①②③④ D.②③④
5.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售为x元,则可卖出(350-10x)件商品,那么商品所赚钱y元与售价x元的函数关系为( )
A. B.
C. D.
6.正方形ABCD的边长为1,点E,F,G,H分别在边AB,BC,CD,DA上,且AE= BF=CG=DH.设小正方形EFGH的面积为y,AE=x,则y关于x的函数图象大致是( ).
A. B.
C. D.
7.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
A.193 B.194 C.195 D.196
8.如图,利用一个直角墙角修建一个的四边形储料场,其中.若新建墙与总长为,则该储料场的最大面积是( )
A. B. C. D.
9.如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<12,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDGF周长的最小值为,其中,判断正确的序号是( )
A.①② B.②③ C.①③ D.②③④
10.已知点,若抛物线与线段有2个不同的交点,则a的取值范围是( )
A.或 B.或
C. D.或
二、填空题
11.如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙长),中间用两道墙隔开.已知计划中的修筑材料可建围墙总长为,设饲养室的一边长为占地总面积为,则
①y与x的函数关系式为 .(不必写出x取值范围)
②三间饲养室的最大总面积为 .
12.如图,一名学生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是,则铅球推出的距离 .
13.教练对小明投掷实心球的训练录像进行了技术分析,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是 m.
14.公园草坪上,自动浇水喷头喷出的水线呈一条抛物线,水线上水珠的离地高度y(米)关于水珠与喷头的水平距离x(米)的函数解析式是.那么水珠的最大离地高度是 米.
15.如图,为世界最大跨度铁路拱桥——贵州北盘江特大桥.如图,已知拱桥曲线呈抛物线,主桥底部跨度米,以为原点,所在直线为轴建立平面直角坐标系,点为抛物线最高点,立柱,,都与轴垂直,,,,若,,和,,均三点共线.则立柱比 ,以及 .
16.如图,正方形EFGH的顶点在边长为2的正方形的边上若设,正方形EFGH的面积为y,则y与x的函数关系为 .
三、解答题
17.如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)在如图的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
18.喜迎新学期,学校要围成一个矩形花圃,花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成,围成的花圃是如图所示的矩形.设边的长为x米,矩形的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)
(2)求花圃的最大面积.
19.用一条长的绳子围成一个矩形,设矩形的一边长为.
(1)若围成的矩形面积为,求的值;
(2)当为何值时围成的矩形面积最大,最大面积是多少?
20.某公司分别在A、B两城生产一批同种产品共100件,A城生产产品的成本y(万元)与产品数量x(件)之间的函数关系为,当时,;当时,.B城生产产品的每件成本为70万元.
(1)求A城生产产品的成本y(万元)与产品数量x(件)之间的函数关系式;
(2)当A、B两城生产这批产品的总成本的和最少时,求A、B两城各生产多少件.
21.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M'.
(1)求抛物线的解析式;
(2)若直线AM'与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
22.已知抛物线L经过点A(-1,0)和B(3,0)与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)平移抛物线L,使平移后的抛物线经过点B,与x轴的另一个交点为Q,与y轴交于点P,同时满足△BPQ是直角三角形,请你写出平移过程并说明理由.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】C
11.【答案】;200
12.【答案】
13.【答案】9
14.【答案】
15.【答案】;
16.【答案】
17.【答案】(1)y=;(2)5小时
18.【答案】(1)
(2)128
19.【答案】(1)的值为或;
(2)当时,面积最大,最大面积为.
20.【答案】(1)解:
(2)解:当A,B两城生产这批产品的总成本的和最少时,A,B两城分别生产20件、80件
21.【答案】(1)y=x2﹣2x﹣3;(2)24;(3)存在,y=(x﹣1)2﹣2或y=﹣(x﹣1)2+2,
22.【答案】(1)解:设抛物线的解析式为y=ax2+bx+c,
把A(-1,0)、B(3,0)、C(0,3)代入y=ax2+bx+c,
得.解得,
∴抛物线的解析式为y=-x2+2x+3.
(2)解:设平移后的抛物线的解析式为:,
∵平移后的抛物线过点,
∴,
∴,
当时,,
∴;
当时:,
解得:,
∴,
∴,,,
∵是直角三角形,分三种情况,
①,即:,
解得:,此时与点重合,不符合题意;
②,即:,
解得:或(不合题意,舍去);
∴,
∵,,
∴将原抛物线先向右平移个单位,再向下平移个单位,得到新的抛物线;
③,即:,
解得或,均不符合题意;
综上:将原抛物线先向右平移个单位,再向下平移个单位,得到新的抛物线,满足题意.
一、单选题
1.如图是抛物线型拱桥,当拱顶高离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m B.2m C.m D.m
2.某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
3.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系,下列对方程的两根与的解释正确的是( )
A.小球的飞行高度为15m时,小球飞行的时间是1s
B.小球飞行时飞行高度为15m,并将继续上升
C.小球从飞出到落地要用4s
D.小球的飞行高度可以达到25m
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t= ;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③ B.①②③ C.①②③④ D.②③④
5.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售为x元,则可卖出(350-10x)件商品,那么商品所赚钱y元与售价x元的函数关系为( )
A. B.
C. D.
6.正方形ABCD的边长为1,点E,F,G,H分别在边AB,BC,CD,DA上,且AE= BF=CG=DH.设小正方形EFGH的面积为y,AE=x,则y关于x的函数图象大致是( ).
A. B.
C. D.
7.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
A.193 B.194 C.195 D.196
8.如图,利用一个直角墙角修建一个的四边形储料场,其中.若新建墙与总长为,则该储料场的最大面积是( )
A. B. C. D.
9.如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1
A.①② B.②③ C.①③ D.②③④
10.已知点,若抛物线与线段有2个不同的交点,则a的取值范围是( )
A.或 B.或
C. D.或
二、填空题
11.如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙长),中间用两道墙隔开.已知计划中的修筑材料可建围墙总长为,设饲养室的一边长为占地总面积为,则
①y与x的函数关系式为 .(不必写出x取值范围)
②三间饲养室的最大总面积为 .
12.如图,一名学生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是,则铅球推出的距离 .
13.教练对小明投掷实心球的训练录像进行了技术分析,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是 m.
14.公园草坪上,自动浇水喷头喷出的水线呈一条抛物线,水线上水珠的离地高度y(米)关于水珠与喷头的水平距离x(米)的函数解析式是.那么水珠的最大离地高度是 米.
15.如图,为世界最大跨度铁路拱桥——贵州北盘江特大桥.如图,已知拱桥曲线呈抛物线,主桥底部跨度米,以为原点,所在直线为轴建立平面直角坐标系,点为抛物线最高点,立柱,,都与轴垂直,,,,若,,和,,均三点共线.则立柱比 ,以及 .
16.如图,正方形EFGH的顶点在边长为2的正方形的边上若设,正方形EFGH的面积为y,则y与x的函数关系为 .
三、解答题
17.如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)在如图的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
18.喜迎新学期,学校要围成一个矩形花圃,花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成,围成的花圃是如图所示的矩形.设边的长为x米,矩形的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)
(2)求花圃的最大面积.
19.用一条长的绳子围成一个矩形,设矩形的一边长为.
(1)若围成的矩形面积为,求的值;
(2)当为何值时围成的矩形面积最大,最大面积是多少?
20.某公司分别在A、B两城生产一批同种产品共100件,A城生产产品的成本y(万元)与产品数量x(件)之间的函数关系为,当时,;当时,.B城生产产品的每件成本为70万元.
(1)求A城生产产品的成本y(万元)与产品数量x(件)之间的函数关系式;
(2)当A、B两城生产这批产品的总成本的和最少时,求A、B两城各生产多少件.
21.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M'.
(1)求抛物线的解析式;
(2)若直线AM'与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
22.已知抛物线L经过点A(-1,0)和B(3,0)与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)平移抛物线L,使平移后的抛物线经过点B,与x轴的另一个交点为Q,与y轴交于点P,同时满足△BPQ是直角三角形,请你写出平移过程并说明理由.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】C
11.【答案】;200
12.【答案】
13.【答案】9
14.【答案】
15.【答案】;
16.【答案】
17.【答案】(1)y=;(2)5小时
18.【答案】(1)
(2)128
19.【答案】(1)的值为或;
(2)当时,面积最大,最大面积为.
20.【答案】(1)解:
(2)解:当A,B两城生产这批产品的总成本的和最少时,A,B两城分别生产20件、80件
21.【答案】(1)y=x2﹣2x﹣3;(2)24;(3)存在,y=(x﹣1)2﹣2或y=﹣(x﹣1)2+2,
22.【答案】(1)解:设抛物线的解析式为y=ax2+bx+c,
把A(-1,0)、B(3,0)、C(0,3)代入y=ax2+bx+c,
得.解得,
∴抛物线的解析式为y=-x2+2x+3.
(2)解:设平移后的抛物线的解析式为:,
∵平移后的抛物线过点,
∴,
∴,
当时,,
∴;
当时:,
解得:,
∴,
∴,,,
∵是直角三角形,分三种情况,
①,即:,
解得:,此时与点重合,不符合题意;
②,即:,
解得:或(不合题意,舍去);
∴,
∵,,
∴将原抛物线先向右平移个单位,再向下平移个单位,得到新的抛物线;
③,即:,
解得或,均不符合题意;
综上:将原抛物线先向右平移个单位,再向下平移个单位,得到新的抛物线,满足题意.
同课章节目录
