专项训练卷(四)欧姆定律的综合计算 2024-2025学年物理人教版九年级全一册(含答案)
文档属性
| 名称 | 专项训练卷(四)欧姆定律的综合计算 2024-2025学年物理人教版九年级全一册(含答案) | 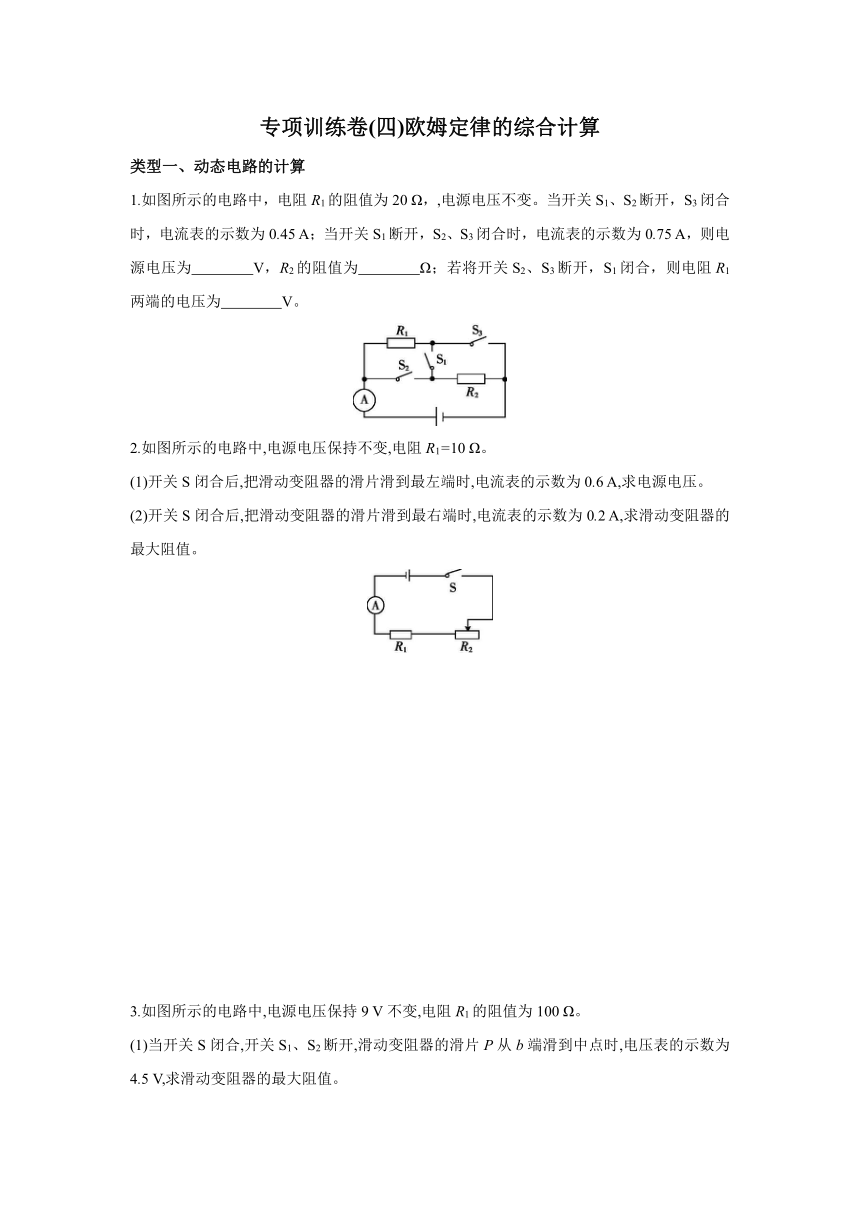 | |
| 格式 | docx | ||
| 文件大小 | 108.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-15 22:29:44 | ||
图片预览



文档简介
专项训练卷(四)欧姆定律的综合计算
类型一、动态电路的计算
1.如图所示的电路中,电阻R1的阻值为20 Ω,,电源电压不变。当开关S1、S2断开,S3闭合时,电流表的示数为0.45 A;当开关S1断开,S2、S3闭合时,电流表的示数为0.75 A,则电源电压为 V,R2的阻值为 Ω;若将开关S2、S3断开,S1闭合,则电阻R1两端的电压为 V。
2.如图所示的电路中,电源电压保持不变,电阻R1=10 Ω。
(1)开关S闭合后,把滑动变阻器的滑片滑到最左端时,电流表的示数为0.6 A,求电源电压。
(2)开关S闭合后,把滑动变阻器的滑片滑到最右端时,电流表的示数为0.2 A,求滑动变阻器的最大阻值。
3.如图所示的电路中,电源电压保持9 V不变,电阻R1的阻值为100 Ω。
(1)当开关S闭合,开关S1、S2断开,滑动变阻器的滑片P从b端滑到中点时,电压表的示数为4.5 V,求滑动变阻器的最大阻值。
(2)当开关S、S1、S2都闭合,滑动变阻器的滑片P滑到b端时,电流表的示数为0.7 A,求电阻R2的阻值。
类型二、含图像的电学计算
4.将电阻R和灯泡L接在图甲所示的电路中,电源电压保持不变。图乙为电阻R和灯泡L的I-U图像。闭合开关S,电流表的示数为0.3 A,则电源电压和电阻R的阻值大小分别是 ( )
A.8 V;6.67 Ω
B.12 V;20 Ω
C.8 V;20 Ω
D.12 V;10 Ω
5.如图甲所示的电路中,电源电压不变。闭合开关S后,滑动变阻器R的滑片P由a端移动到中点时,测得电阻R0两端的电压U与通过电阻R0的电流I的变化关系如图乙所示。求:
(1)电源电压。
(2)电阻R0的阻值。
(3)滑动变阻器R的最大阻值。
类型三、电路安全及取值范围的计算
6.甲、乙两个定值电阻,甲标有“10 Ω 1 A”的字样,乙标有“20 Ω 0.5 A”的字样。若把它们串联起来使用,则该串联电路中允许通过的最大电流为 A,两端允许加的最大电压是 V;若把它们并联起来使用,则该并联电路两端允许加的最大电压为 V,干路中的最大电流是 A。
7.小强同学按如图所示的电路连接电学器材进行电学实验。已知电源电压为6 V且保持不变,电流表的量程为0~0.6 A,电压表的量程为0~3 V,电阻R1的阻值为10 Ω,滑动变阻器R2的规格为“20 Ω 0.5 A”。将开关S闭合后,为保证电路中各元件正常工作,以下说法正确的是 ( )
A.滑动变阻器R2接入电路中的最小阻值为5 Ω
B.电压表示数变化量的最大值为1 V
C.通过电阻R1的电流最大值为0.4 A
D.滑动变阻器R2的调节范围为0~20 Ω
8.如图所示,R2为标有“50 Ω 2 A”字样的滑动变阻器,闭合开关后,电压表的示数为6 V,电流表A1的示数为0.5 A,电流表A2的示数为2 A。
(1)求电阻R1的阻值。
(2)求滑动变阻器R2接入电路中的电阻。
(3)电流表A1的量程是0~0.6 A,电流表A2的量程是0~3 A。为了使电路元件不损坏,滑动变阻器接入电路中的最小电阻是多少
9.为了改善路况,某科研小组研制出了一种新型材料制作的井盖,大大提高了井盖的抗压能力。某同学为了测试该材料的抗压能力,取下来一小块样品进行抗压测试。如图甲所示,电源电压为24 V,定值电阻R0=20 Ω,将该材料样品(不计质量)平放在压力传感器上,闭合开关S,经过多次压力测试,压力传感器的电阻R随压力F的变化关系如图乙所示。
(1)求压力为0时,电流表的示数。
(2)经过多次实验,当电流表的示数为0.6 A时,该材料即将破损,则该材料承受的最大压力是多大
(3)小红想继续将此装置改装为磅秤,如果电流表的量程为0~1 A,该磅秤能测量的最大质量为多少 (g取10 N/kg)
参考答案
1.9 30 3.6
解析:当开关S1、S2断开,S3闭合时,电路为电阻R1的简单电路,此时电路中的电流I1=0.45 A,则由欧姆定律可得,电源电压U=I1R1=0.45 A×20 Ω=9 V;当开关S1断开,S2、S3闭合时,电阻R1、R2并联,电流表测量电路中的电流,此时通过电阻R2的电流I2=I-I1=0.75 A-0.45 A=0.3 A,则电阻R2===30 Ω;当开关S2、S3断开,S1闭合时,电阻R1、R2串联,此时电路中的电流I'===0.18 A,电阻R1两端的电压U1=I'R1=0.18 A×20 Ω=3.6 V。
2.解:(1)由电路图可知,开关S闭合后,把滑动变阻器的滑片滑到最左端时,只有电阻R1接入电路中,由欧姆定律可得,电源电压U=U1=IR1=0.6 A×10 Ω=6 V。
(2)开关S闭合后,把滑动变阻器的滑片滑到最右端时,滑动变阻器接入电路中的阻值最大,电阻R1与滑动变阻器R2串联,电流表测量电路中的电流,由欧姆定律可得,电阻R1两端的电压U1'=I'R1=0.2 A×10 Ω=2 V,则滑动变阻器R2两端的电压U2=U-U1'=6 V-2 V=4 V,滑动变阻器的最大阻值R2===20 Ω。
3.解:(1)当开关S闭合,开关S1、S2断开,滑片P从b端滑到中点时,电阻R1与滑动变阻器R3串联,电压表测量电阻R1两端的电压,则电路中的电流I=I1===0.45 A,滑动变阻器R3两端的电压U3=U-U1=9 V-4.5 V=4.5 V,则此时滑动变阻器接入电路中的阻值R===10 Ω,滑动变阻器的最大阻值R3=2R=2×10 Ω=20 Ω。
(2)开关S、S1、S2都闭合,滑动变阻器的滑片P滑到b端时,电阻R1被短路,滑动变阻器R3与电阻R2并联,电流表测量干路中的电流,则U=U3'=U2=9 V,通过滑动变阻器的电流I3===0.45 A,通过电阻R2的电流I2=I'-I3=0.7 A-0.45 A=0.25 A,则电阻R2===36 Ω。
4.C
解析:电阻R为定值电阻,故通过定值电阻的电流随电压的变化关系为一条倾斜的直线,根据图像可得,电阻R===20 Ω;由图甲可知,定值电阻R和灯泡L串联,电流表测量电路中的电流,由图像可知,电路中的电流I=0.3 A时,定值电阻R和灯泡L两端的电压分别为UL=2 V,UR=6 V,则电源电压U=UL+UR=2 V+6 V=8 V。
5.解:(1)由图甲可知,当滑动变阻器R的滑片P在a端时,滑动变阻器接入电路中的电阻为0 Ω,电路为电阻R0的简单电路,电路中的电流最大,由图乙可知,电源电压U=12 V。
(2)由图乙可知,滑动变阻器的滑片P在a端时,电路中的电流I=1.5 A,根据欧姆定律可得,电阻R0的阻值R0===8 Ω。
(3)由图甲可知,滑动变阻器R的滑片P移动到b端时,电阻R0与滑动变阻器R串联,此时滑动变阻器接入电路中的电阻最大,电压表测量电阻R0两端的电压,即U0=4 V,由串联电路中电压的特点可知,滑动变阻器R两端的电压UR=U-U0=12 V-4 V=8 V,由图乙可知,此时电路中的电流I'=0.5 A,所以滑动变阻器R的最大阻值Rmax===16 Ω。
6. 0.5 15 10 1.5
解析:因串联电路中各处的电流相等,所以两只电阻串联时,电路中的最大电流I=I乙=0.5 A,因串联电路中总电阻等于各分电阻之和,所以由I=可得,两端允许加的最大电压U=I(R甲+R乙)=0.5 A×(10 Ω+20 Ω)=15 V;由I=可得,两电阻两端允许所加的最大电压U甲=I甲R甲=1 A×10 Ω=10 V,U乙=I乙R乙=0.5 A×20 Ω=10 V,因并联电路中各支路两端的电压相等,所以两只电阻并联时,电路中的最大电压U'=10 V。此时通过乙的电流为0.5 A,通过甲的电流为1 A,因为并联电路中干路电流等于各支路电流之和,所以干路最大电流I=I甲'+I乙=1 A+0.5 A=1.5 A。
7.B
解析:由于电流表的量程为0~0.6 A,滑动变阻器R2允许通过的最大电流I2max=0.5 A,所以电路中允许通过的最大电流不能超过0.5 A,又因为电压表的量程为0~3 V,滑动变阻器的滑片P不能移动到最左端(即滑动变阻器连入电路中的电阻不能为0),当电阻R1两端的电压U1=3 V时,电路中的电流I===0.3 A,所以电路中的最大电流为0.3 A,即当U1=3 V时,通过电阻R1的电流最大值为0.3 A,故C选项错误;此时滑动变阻器R2两端的电压U2=U-U1=6 V-3 V=3 V,滑动变阻器R2接入电路中的最小电阻R2min===10 Ω,故 A、D选项错误;当滑动变阻器R2的滑片P在最右端(即滑动变阻器连入电路中的电阻为20 Ω)时,此时电路中的电阻最大,电流最小,则Imin====0.2 A,由欧姆定律可得,U1min=IminR1=0.2 A×10 Ω=2 V,则电压表示数变化量的最大值ΔU=U1-Umin=3 V-2 V=1 V,故B选项正确。
8.解:(1)由电路图可知,电阻R1与滑动变阻器R2并联,电压表测量电源电压U,电流表 A2测量干路中的电流I,电流表 A1测量电阻R1所在支路的电流I1,根据欧姆定律可得,电阻R1的阻值R1===12 Ω。
(2)因为并联电路干路中的电流等于各支路电流之和,所以通过滑动变阻器R2的电流I2=I-I1=2 A-0.5 A=1.5 A,滑动变阻器R2接入电路中的电阻R2===4 Ω。
(3)因为并联电路中各支路独立工作、互不影响,所以移动滑动变阻器R2的滑片时,通过电阻R1的电流不变,即I1=0.5 A。若电流表 A2的示数为3 A,此时通过滑动变阻器R2的电流I2'=Imax-I1=3 A-0.5 A=2.5 A,因为滑动变阻器R2的规格为“50 Ω 2 A”,所以通过滑动变阻器R2的电流最大为I2max=2 A,则滑动变阻器接入电路中的电阻最小值R2min===3 Ω。
9.解:(1)由图甲可知,定值电阻R0与压力传感器串联,电流表测量电路中的电流。由图乙可知,当压力为0时,压力传感器的电阻为100 Ω,电流表的示数I====0.2 A。
(2)当电流表的示数为0.6 A时,电路中的总电阻R总'===40 Ω,因串联电路中的总电阻等于各分电阻之和,所以压力传感器的阻值R'=R总'-R0=40 Ω-20 Ω=20 Ω,由图乙可知,当压力传感器的阻值为20 Ω时,压力大小为6000 N。
(3)根据电流表的量程可知,电路中的最大电流为1 A,此时电路中的总电阻R总″===24 Ω,压力传感器的阻值R″=R总″-R0=24 Ω-20 Ω=4 Ω,由图乙可知,此时磅秤受到的压力为10000 N,即所测物体所受的最大重力G=10000 N,则所测物体的最大质量mmax===1000 kg。
类型一、动态电路的计算
1.如图所示的电路中,电阻R1的阻值为20 Ω,,电源电压不变。当开关S1、S2断开,S3闭合时,电流表的示数为0.45 A;当开关S1断开,S2、S3闭合时,电流表的示数为0.75 A,则电源电压为 V,R2的阻值为 Ω;若将开关S2、S3断开,S1闭合,则电阻R1两端的电压为 V。
2.如图所示的电路中,电源电压保持不变,电阻R1=10 Ω。
(1)开关S闭合后,把滑动变阻器的滑片滑到最左端时,电流表的示数为0.6 A,求电源电压。
(2)开关S闭合后,把滑动变阻器的滑片滑到最右端时,电流表的示数为0.2 A,求滑动变阻器的最大阻值。
3.如图所示的电路中,电源电压保持9 V不变,电阻R1的阻值为100 Ω。
(1)当开关S闭合,开关S1、S2断开,滑动变阻器的滑片P从b端滑到中点时,电压表的示数为4.5 V,求滑动变阻器的最大阻值。
(2)当开关S、S1、S2都闭合,滑动变阻器的滑片P滑到b端时,电流表的示数为0.7 A,求电阻R2的阻值。
类型二、含图像的电学计算
4.将电阻R和灯泡L接在图甲所示的电路中,电源电压保持不变。图乙为电阻R和灯泡L的I-U图像。闭合开关S,电流表的示数为0.3 A,则电源电压和电阻R的阻值大小分别是 ( )
A.8 V;6.67 Ω
B.12 V;20 Ω
C.8 V;20 Ω
D.12 V;10 Ω
5.如图甲所示的电路中,电源电压不变。闭合开关S后,滑动变阻器R的滑片P由a端移动到中点时,测得电阻R0两端的电压U与通过电阻R0的电流I的变化关系如图乙所示。求:
(1)电源电压。
(2)电阻R0的阻值。
(3)滑动变阻器R的最大阻值。
类型三、电路安全及取值范围的计算
6.甲、乙两个定值电阻,甲标有“10 Ω 1 A”的字样,乙标有“20 Ω 0.5 A”的字样。若把它们串联起来使用,则该串联电路中允许通过的最大电流为 A,两端允许加的最大电压是 V;若把它们并联起来使用,则该并联电路两端允许加的最大电压为 V,干路中的最大电流是 A。
7.小强同学按如图所示的电路连接电学器材进行电学实验。已知电源电压为6 V且保持不变,电流表的量程为0~0.6 A,电压表的量程为0~3 V,电阻R1的阻值为10 Ω,滑动变阻器R2的规格为“20 Ω 0.5 A”。将开关S闭合后,为保证电路中各元件正常工作,以下说法正确的是 ( )
A.滑动变阻器R2接入电路中的最小阻值为5 Ω
B.电压表示数变化量的最大值为1 V
C.通过电阻R1的电流最大值为0.4 A
D.滑动变阻器R2的调节范围为0~20 Ω
8.如图所示,R2为标有“50 Ω 2 A”字样的滑动变阻器,闭合开关后,电压表的示数为6 V,电流表A1的示数为0.5 A,电流表A2的示数为2 A。
(1)求电阻R1的阻值。
(2)求滑动变阻器R2接入电路中的电阻。
(3)电流表A1的量程是0~0.6 A,电流表A2的量程是0~3 A。为了使电路元件不损坏,滑动变阻器接入电路中的最小电阻是多少
9.为了改善路况,某科研小组研制出了一种新型材料制作的井盖,大大提高了井盖的抗压能力。某同学为了测试该材料的抗压能力,取下来一小块样品进行抗压测试。如图甲所示,电源电压为24 V,定值电阻R0=20 Ω,将该材料样品(不计质量)平放在压力传感器上,闭合开关S,经过多次压力测试,压力传感器的电阻R随压力F的变化关系如图乙所示。
(1)求压力为0时,电流表的示数。
(2)经过多次实验,当电流表的示数为0.6 A时,该材料即将破损,则该材料承受的最大压力是多大
(3)小红想继续将此装置改装为磅秤,如果电流表的量程为0~1 A,该磅秤能测量的最大质量为多少 (g取10 N/kg)
参考答案
1.9 30 3.6
解析:当开关S1、S2断开,S3闭合时,电路为电阻R1的简单电路,此时电路中的电流I1=0.45 A,则由欧姆定律可得,电源电压U=I1R1=0.45 A×20 Ω=9 V;当开关S1断开,S2、S3闭合时,电阻R1、R2并联,电流表测量电路中的电流,此时通过电阻R2的电流I2=I-I1=0.75 A-0.45 A=0.3 A,则电阻R2===30 Ω;当开关S2、S3断开,S1闭合时,电阻R1、R2串联,此时电路中的电流I'===0.18 A,电阻R1两端的电压U1=I'R1=0.18 A×20 Ω=3.6 V。
2.解:(1)由电路图可知,开关S闭合后,把滑动变阻器的滑片滑到最左端时,只有电阻R1接入电路中,由欧姆定律可得,电源电压U=U1=IR1=0.6 A×10 Ω=6 V。
(2)开关S闭合后,把滑动变阻器的滑片滑到最右端时,滑动变阻器接入电路中的阻值最大,电阻R1与滑动变阻器R2串联,电流表测量电路中的电流,由欧姆定律可得,电阻R1两端的电压U1'=I'R1=0.2 A×10 Ω=2 V,则滑动变阻器R2两端的电压U2=U-U1'=6 V-2 V=4 V,滑动变阻器的最大阻值R2===20 Ω。
3.解:(1)当开关S闭合,开关S1、S2断开,滑片P从b端滑到中点时,电阻R1与滑动变阻器R3串联,电压表测量电阻R1两端的电压,则电路中的电流I=I1===0.45 A,滑动变阻器R3两端的电压U3=U-U1=9 V-4.5 V=4.5 V,则此时滑动变阻器接入电路中的阻值R===10 Ω,滑动变阻器的最大阻值R3=2R=2×10 Ω=20 Ω。
(2)开关S、S1、S2都闭合,滑动变阻器的滑片P滑到b端时,电阻R1被短路,滑动变阻器R3与电阻R2并联,电流表测量干路中的电流,则U=U3'=U2=9 V,通过滑动变阻器的电流I3===0.45 A,通过电阻R2的电流I2=I'-I3=0.7 A-0.45 A=0.25 A,则电阻R2===36 Ω。
4.C
解析:电阻R为定值电阻,故通过定值电阻的电流随电压的变化关系为一条倾斜的直线,根据图像可得,电阻R===20 Ω;由图甲可知,定值电阻R和灯泡L串联,电流表测量电路中的电流,由图像可知,电路中的电流I=0.3 A时,定值电阻R和灯泡L两端的电压分别为UL=2 V,UR=6 V,则电源电压U=UL+UR=2 V+6 V=8 V。
5.解:(1)由图甲可知,当滑动变阻器R的滑片P在a端时,滑动变阻器接入电路中的电阻为0 Ω,电路为电阻R0的简单电路,电路中的电流最大,由图乙可知,电源电压U=12 V。
(2)由图乙可知,滑动变阻器的滑片P在a端时,电路中的电流I=1.5 A,根据欧姆定律可得,电阻R0的阻值R0===8 Ω。
(3)由图甲可知,滑动变阻器R的滑片P移动到b端时,电阻R0与滑动变阻器R串联,此时滑动变阻器接入电路中的电阻最大,电压表测量电阻R0两端的电压,即U0=4 V,由串联电路中电压的特点可知,滑动变阻器R两端的电压UR=U-U0=12 V-4 V=8 V,由图乙可知,此时电路中的电流I'=0.5 A,所以滑动变阻器R的最大阻值Rmax===16 Ω。
6. 0.5 15 10 1.5
解析:因串联电路中各处的电流相等,所以两只电阻串联时,电路中的最大电流I=I乙=0.5 A,因串联电路中总电阻等于各分电阻之和,所以由I=可得,两端允许加的最大电压U=I(R甲+R乙)=0.5 A×(10 Ω+20 Ω)=15 V;由I=可得,两电阻两端允许所加的最大电压U甲=I甲R甲=1 A×10 Ω=10 V,U乙=I乙R乙=0.5 A×20 Ω=10 V,因并联电路中各支路两端的电压相等,所以两只电阻并联时,电路中的最大电压U'=10 V。此时通过乙的电流为0.5 A,通过甲的电流为1 A,因为并联电路中干路电流等于各支路电流之和,所以干路最大电流I=I甲'+I乙=1 A+0.5 A=1.5 A。
7.B
解析:由于电流表的量程为0~0.6 A,滑动变阻器R2允许通过的最大电流I2max=0.5 A,所以电路中允许通过的最大电流不能超过0.5 A,又因为电压表的量程为0~3 V,滑动变阻器的滑片P不能移动到最左端(即滑动变阻器连入电路中的电阻不能为0),当电阻R1两端的电压U1=3 V时,电路中的电流I===0.3 A,所以电路中的最大电流为0.3 A,即当U1=3 V时,通过电阻R1的电流最大值为0.3 A,故C选项错误;此时滑动变阻器R2两端的电压U2=U-U1=6 V-3 V=3 V,滑动变阻器R2接入电路中的最小电阻R2min===10 Ω,故 A、D选项错误;当滑动变阻器R2的滑片P在最右端(即滑动变阻器连入电路中的电阻为20 Ω)时,此时电路中的电阻最大,电流最小,则Imin====0.2 A,由欧姆定律可得,U1min=IminR1=0.2 A×10 Ω=2 V,则电压表示数变化量的最大值ΔU=U1-Umin=3 V-2 V=1 V,故B选项正确。
8.解:(1)由电路图可知,电阻R1与滑动变阻器R2并联,电压表测量电源电压U,电流表 A2测量干路中的电流I,电流表 A1测量电阻R1所在支路的电流I1,根据欧姆定律可得,电阻R1的阻值R1===12 Ω。
(2)因为并联电路干路中的电流等于各支路电流之和,所以通过滑动变阻器R2的电流I2=I-I1=2 A-0.5 A=1.5 A,滑动变阻器R2接入电路中的电阻R2===4 Ω。
(3)因为并联电路中各支路独立工作、互不影响,所以移动滑动变阻器R2的滑片时,通过电阻R1的电流不变,即I1=0.5 A。若电流表 A2的示数为3 A,此时通过滑动变阻器R2的电流I2'=Imax-I1=3 A-0.5 A=2.5 A,因为滑动变阻器R2的规格为“50 Ω 2 A”,所以通过滑动变阻器R2的电流最大为I2max=2 A,则滑动变阻器接入电路中的电阻最小值R2min===3 Ω。
9.解:(1)由图甲可知,定值电阻R0与压力传感器串联,电流表测量电路中的电流。由图乙可知,当压力为0时,压力传感器的电阻为100 Ω,电流表的示数I====0.2 A。
(2)当电流表的示数为0.6 A时,电路中的总电阻R总'===40 Ω,因串联电路中的总电阻等于各分电阻之和,所以压力传感器的阻值R'=R总'-R0=40 Ω-20 Ω=20 Ω,由图乙可知,当压力传感器的阻值为20 Ω时,压力大小为6000 N。
(3)根据电流表的量程可知,电路中的最大电流为1 A,此时电路中的总电阻R总″===24 Ω,压力传感器的阻值R″=R总″-R0=24 Ω-20 Ω=4 Ω,由图乙可知,此时磅秤受到的压力为10000 N,即所测物体所受的最大重力G=10000 N,则所测物体的最大质量mmax===1000 kg。
同课章节目录
- 第十三章 内能
- 第1节 分子热运动
- 第2节 内能
- 第3节 比热容
- 第十四章 内能的利用
- 第1节 热机
- 第2节 热机的效率
- 第3节 能量的转化和守恒
- 第十五章 电流和电路
- 第1节 两种电荷
- 第2节 电流和电路
- 第3节 串联和并联
- 第4节 电流的测量
- 第5节 串、并联电路中电流的规律
- 第十六章 电压 电阻
- 第1节 电压
- 第2节 串、并联电路电压的规律
- 第3节 电阻
- 第4节 变阻器
- 第十七章 欧姆定律
- 第1节 电流与电压和电阻的关系
- 第2节 欧姆定律
- 第3节 电阻的测量
- 第4节 欧姆定律在串、并联电路中的应用
- 第十八章 电功率
- 第1节 电能 电功
- 第2节 电功率
- 第3节 测量小灯泡的电功率
- 第4节 焦耳定律
- 第十九章 生活用电
- 第1节 家庭电路
- 第2节 家庭电路电流过大的原因
- 第3节 安全用电
- 第二十章 电与磁
- 第1节 磁现象 磁场
- 第2节 电生磁
- 第3节 电磁铁 电磁继电器
- 第4节 电动机
- 第5节 磁生电
- 第二十一章 信息的传递
- 第1节 现代顺风耳──电话
- 第2节 电磁波的海洋
- 第3节 广播、电视和移动通信
- 第4节 越来越宽的信息之路
- 第二十二章 能源与可持续发展
- 第1节 能源
- 第2节 核能
- 第3节 太阳能
- 第4节 能源与可持续发展
