湘教版数学八年级上册 专项练习(一) 分式、一元一次不等式(组)(含答案)
文档属性
| 名称 | 湘教版数学八年级上册 专项练习(一) 分式、一元一次不等式(组)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 11:21:58 | ||
图片预览


文档简介
专项练习(一)分式、一元一次不等式(组)
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题4分,共48分)
1. 满足x+2019>0的最小整数解是 ( )
A. -2 020 B. -2 019 C. -2 018 D. 2 020
2. 下列分式 中,最简分式的个数是 ( )
A. 1 B. 2 C. 3 D. 4
3. 下列说法正确的是 ( )
A. x=3.14是不等式2x-5>0的一个解 是一元一次不等式
C. 不等式组 有一个正整数解 D. 不等式-2x+3>0的解集是
4. 解分式方程 时,去分母可得 ( )
A. 1-3(x-2)=4 B. 1-3(x-2)=-4
C. ﹣1﹣3(2﹣x)=﹣4 D. 1-3(2-x)=4
5. 我们定义 例如 若x满足 则整数x的值有 ( )
A. 0个 B. 1个 C. 2个 D. 3 个
6. 若不等式组 的解集中每一个x值均不在2≤x≤5的范围内,则m的取值范围是( )
A. m<1或m>5 B. m≤1或m≥5 C. m>1或m<5 D. m≤1
7. 已知x>y,且xy<0,a为任意实数,则下列式子正确的是 ( )
C. 2a-3x<2a-3y D. a+x>a-y
8. 去分母解关于x的方程 时产生增根,则m的值为 ( )
A. 1 B. ﹣1 C. 3 D. ﹣3
9. 能使得不等式3(x-1)<5x+2与 都成立的正整数x的个数有 ( )
A. 3个 B. 4个 C. 5个 D. 6个
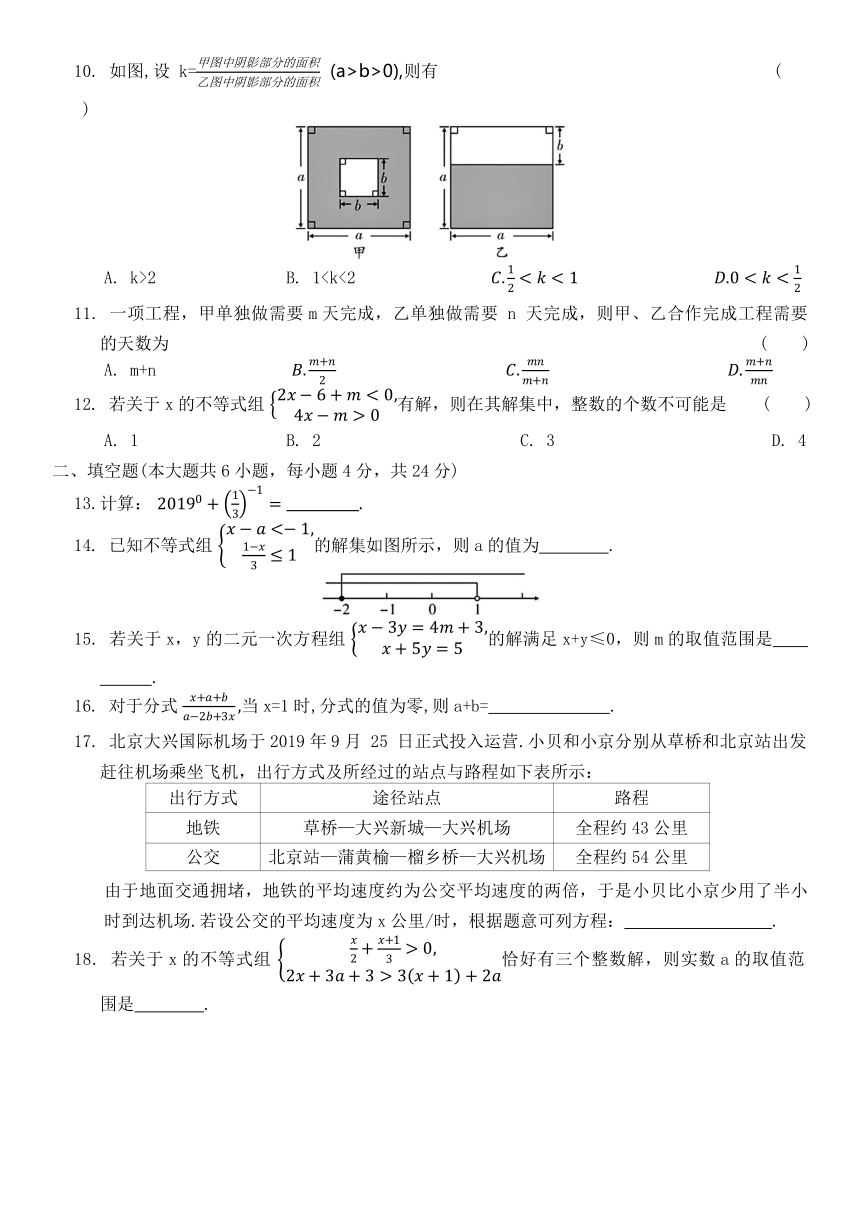
10. 如图,设 k= (a>b>0),则有 ( )
A. k>2 B. 111. 一项工程,甲单独做需要m天完成,乙单独做需要 n 天完成,则甲、乙合作完成工程需要的天数为 ( )
A. m+n
12. 若关于x的不等式组 有解,则在其解集中,整数的个数不可能是 ( )
A. 1 B. 2 C. 3 D. 4
二、填空题(本大题共6小题,每小题4分,共24分)
13.计算:
14. 已知不等式组 的解集如图所示,则a的值为 .
15. 若关于x,y的二元一次方程组 的解满足x+y≤0,则m的取值范围是 .
16. 对于分式 当x=1时,分式的值为零,则a+b= .
17. 北京大兴国际机场于2019年9月 25 日正式投入运营.小贝和小京分别从草桥和北京站出发赶往机场乘坐飞机,出行方式及所经过的站点与路程如下表所示:
出行方式 途径站点 路程
地铁 草桥—大兴新城—大兴机场 全程约43公里
公交 北京站—蒲黄榆—榴乡桥—大兴机场 全程约54公里
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小贝比小京少用了半小时到达机场.若设公交的平均速度为x公里/时,根据题意可列方程: .
18. 若关于x的不等式组 恰好有三个整数解,则实数a的取值范围是 .
三、解答题(共48分)
19. (6分)已知m是不等式 的一个负整数解,请求出代数式 的值.
20. (10分)已知:x,y满足
(1)用含x的代数式表示y,结果为 .
(2)若y满足 ,求x 的取值范围.
(3)若x,y满足 且 ,求a的取值范围.
21. (10分)(1)化简:
(2)设 为非零常数,对于每一个有意义的x值,都有一个S的值对应,如下表:
x -3 -2 -1 l 3 5 6 7 ...
S 2 2 ...
仔细观察上表,能直接得出方程 的解为 .
22. (10分)例:已知: 求代数式 的值.
解:因为 所以 即 所以
根据材料回答问题:
(1)若 求 的值.
(2)解分式方程组
23. (12分)在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用3 000 元购进医用口罩若干个,第二次又用3000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25 倍,购进的数量比第一次少200个.
(1)求第一次和第二次分别购进的医用口罩数量为多少个
(2)药店第一次购进口罩后,先以每个4元的价格出售,卖出了a个后购进第二批同款口罩,由于进价提高了,药店将口罩的售价也提升至每个4.5元继续销售,卖出了b个后.因当地医院医疗物资紧缺,将其已获得口罩销售收入6 400元和剩余全部的口罩捐赠给了医院.请问药店捐赠口罩至少有多少个 (销售收入=售价×数量)
专项练习(一)分式、一元一次不等式(组)
1. C 2. B 3. A 4. B 5. B 6. B 7. C8. D 9. B10. B11. C 12. C
13. 4 14. 2 15. m≤-2 16. -1且
18. 219. 解:
解不等式 得
∵m是不等式的一个负整数解,. 或 或
∵当 或 时,分式无意义,
当 时,原式
20. 解: 故答案为:
(2)根据题意,得 解得
(3)联立方程组 解得
即 解得
21. 解:(1)原式
(2)由(1)得 当 时, 即 又 即 或 解得 或 .故答案为:7或
22. 解: 即
(2)由题意,得
令 则
解方程组,得
23. 解:(1)设第一次购进医用口罩的数量为x个,则第二次购进医用口罩的数量为( )个,由题意,得 解得 则
答:第一次和第二次分别购进的医用口罩数量为1 000个和800 个.
(2)由(1)可知两次购进口罩共 (个),由题意,得
∴剩余口罩为
即 ∵a,b是整数,
∴b是8的倍数,∴b的最小值是536,
答:药店捐赠口罩至少有267个.
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题4分,共48分)
1. 满足x+2019>0的最小整数解是 ( )
A. -2 020 B. -2 019 C. -2 018 D. 2 020
2. 下列分式 中,最简分式的个数是 ( )
A. 1 B. 2 C. 3 D. 4
3. 下列说法正确的是 ( )
A. x=3.14是不等式2x-5>0的一个解 是一元一次不等式
C. 不等式组 有一个正整数解 D. 不等式-2x+3>0的解集是
4. 解分式方程 时,去分母可得 ( )
A. 1-3(x-2)=4 B. 1-3(x-2)=-4
C. ﹣1﹣3(2﹣x)=﹣4 D. 1-3(2-x)=4
5. 我们定义 例如 若x满足 则整数x的值有 ( )
A. 0个 B. 1个 C. 2个 D. 3 个
6. 若不等式组 的解集中每一个x值均不在2≤x≤5的范围内,则m的取值范围是( )
A. m<1或m>5 B. m≤1或m≥5 C. m>1或m<5 D. m≤1
7. 已知x>y,且xy<0,a为任意实数,则下列式子正确的是 ( )
C. 2a-3x<2a-3y D. a+x>a-y
8. 去分母解关于x的方程 时产生增根,则m的值为 ( )
A. 1 B. ﹣1 C. 3 D. ﹣3
9. 能使得不等式3(x-1)<5x+2与 都成立的正整数x的个数有 ( )
A. 3个 B. 4个 C. 5个 D. 6个
10. 如图,设 k= (a>b>0),则有 ( )
A. k>2 B. 1
A. m+n
12. 若关于x的不等式组 有解,则在其解集中,整数的个数不可能是 ( )
A. 1 B. 2 C. 3 D. 4
二、填空题(本大题共6小题,每小题4分,共24分)
13.计算:
14. 已知不等式组 的解集如图所示,则a的值为 .
15. 若关于x,y的二元一次方程组 的解满足x+y≤0,则m的取值范围是 .
16. 对于分式 当x=1时,分式的值为零,则a+b= .
17. 北京大兴国际机场于2019年9月 25 日正式投入运营.小贝和小京分别从草桥和北京站出发赶往机场乘坐飞机,出行方式及所经过的站点与路程如下表所示:
出行方式 途径站点 路程
地铁 草桥—大兴新城—大兴机场 全程约43公里
公交 北京站—蒲黄榆—榴乡桥—大兴机场 全程约54公里
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小贝比小京少用了半小时到达机场.若设公交的平均速度为x公里/时,根据题意可列方程: .
18. 若关于x的不等式组 恰好有三个整数解,则实数a的取值范围是 .
三、解答题(共48分)
19. (6分)已知m是不等式 的一个负整数解,请求出代数式 的值.
20. (10分)已知:x,y满足
(1)用含x的代数式表示y,结果为 .
(2)若y满足 ,求x 的取值范围.
(3)若x,y满足 且 ,求a的取值范围.
21. (10分)(1)化简:
(2)设 为非零常数,对于每一个有意义的x值,都有一个S的值对应,如下表:
x -3 -2 -1 l 3 5 6 7 ...
S 2 2 ...
仔细观察上表,能直接得出方程 的解为 .
22. (10分)例:已知: 求代数式 的值.
解:因为 所以 即 所以
根据材料回答问题:
(1)若 求 的值.
(2)解分式方程组
23. (12分)在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用3 000 元购进医用口罩若干个,第二次又用3000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25 倍,购进的数量比第一次少200个.
(1)求第一次和第二次分别购进的医用口罩数量为多少个
(2)药店第一次购进口罩后,先以每个4元的价格出售,卖出了a个后购进第二批同款口罩,由于进价提高了,药店将口罩的售价也提升至每个4.5元继续销售,卖出了b个后.因当地医院医疗物资紧缺,将其已获得口罩销售收入6 400元和剩余全部的口罩捐赠给了医院.请问药店捐赠口罩至少有多少个 (销售收入=售价×数量)
专项练习(一)分式、一元一次不等式(组)
1. C 2. B 3. A 4. B 5. B 6. B 7. C8. D 9. B10. B11. C 12. C
13. 4 14. 2 15. m≤-2 16. -1且
18. 2
解不等式 得
∵m是不等式的一个负整数解,. 或 或
∵当 或 时,分式无意义,
当 时,原式
20. 解: 故答案为:
(2)根据题意,得 解得
(3)联立方程组 解得
即 解得
21. 解:(1)原式
(2)由(1)得 当 时, 即 又 即 或 解得 或 .故答案为:7或
22. 解: 即
(2)由题意,得
令 则
解方程组,得
23. 解:(1)设第一次购进医用口罩的数量为x个,则第二次购进医用口罩的数量为( )个,由题意,得 解得 则
答:第一次和第二次分别购进的医用口罩数量为1 000个和800 个.
(2)由(1)可知两次购进口罩共 (个),由题意,得
∴剩余口罩为
即 ∵a,b是整数,
∴b是8的倍数,∴b的最小值是536,
答:药店捐赠口罩至少有267个.
同课章节目录
