湘教版数学八年级上册 专项练习(二) 三角形(含答案)
文档属性
| 名称 | 湘教版数学八年级上册 专项练习(二) 三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 886.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 11:26:00 | ||
图片预览


文档简介
专项练习(二)三角形
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题4分,共48分)
1. 在下列长度的三条线段中,不能组成三角形的是 ( )
A. 2cm ,3cm,4 cm B. 3cm,6cm,6cm C. 2cm,2cm,6 cm D. 5cm,6cm,7 cm
2. 下列命题中,是真命题的是 ( )
A. 等腰三角形的角平分线、中线和高重合
B. 若三角形有两个角相等,那么这两个角所对的边也相等
C. 等腰三角形任意两角都相等
D. 等腰三角形一定是锐角三角形
3. 如图,AD是△ABC的外角∠EAC 的平分线,AD∥BC,∠B=32°,则∠C 的度数是 ( )
A. 64° B. 32° C. 30° D. 40°
4. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是 ( )
A.∠A=∠D B. AC=DF C. AB=DE D. BF=EC
5. 如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是 ( )
A. 20° B. 35° C. 40° D. 70°
6. 三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为 ( )
A. 90° B. 60° C. 45° D. 30°
7. 通过如下尺规作图,能确定点D是边BC 中点的是 ( )
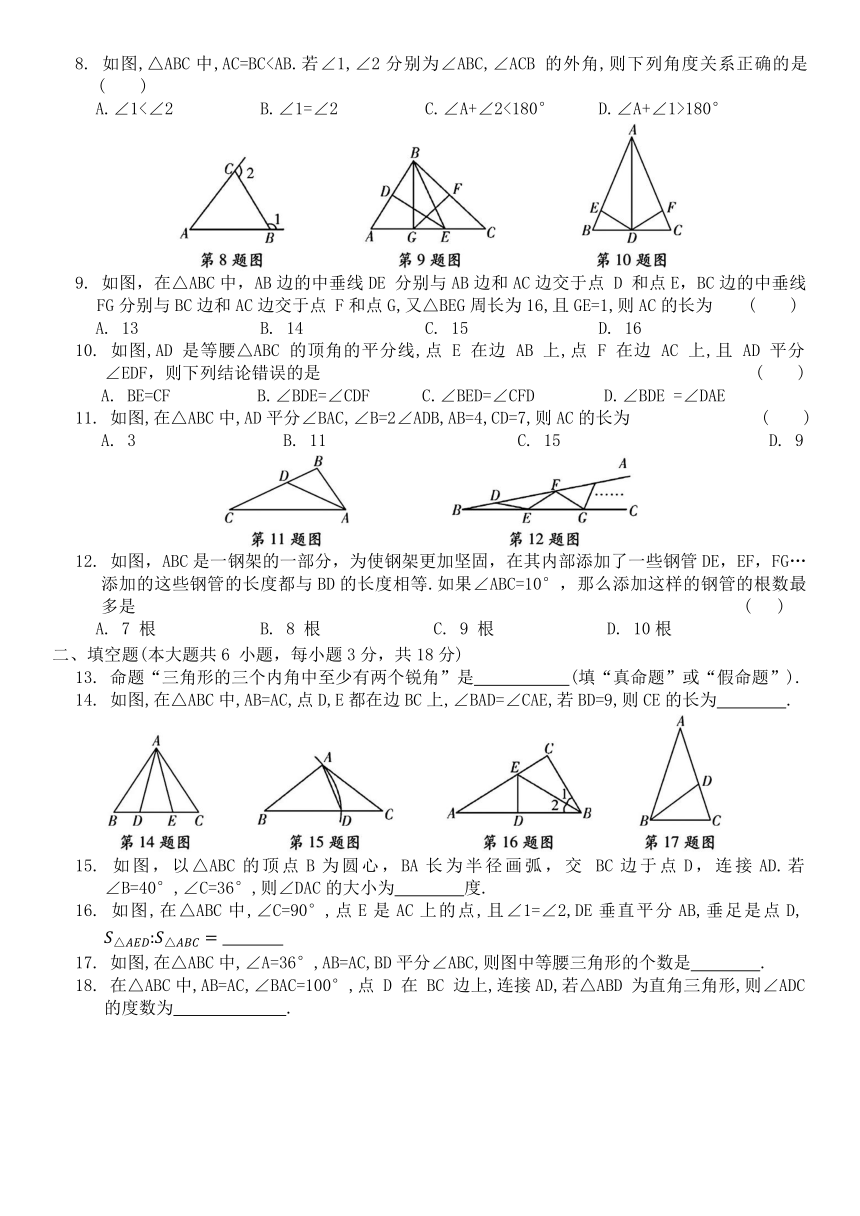
8. 如图,△ABC中,AC=BCA.∠1<∠2 B.∠1=∠2 C.∠A+∠2<180° D.∠A+∠1>180°
9. 如图,在△ABC中,AB边的中垂线DE 分别与AB边和AC边交于点 D 和点E,BC边的中垂线FG分别与BC边和AC边交于点 F和点G,又△BEG周长为16,且GE=1,则AC的长为 ( )
A. 13 B. 14 C. 15 D. 16
10. 如图,AD 是等腰△ABC 的顶角的平分线,点 E 在边 AB 上,点 F 在边 AC 上,且 AD 平分 ∠EDF,则下列结论错误的是 ( )
A. BE=CF B.∠BDE=∠CDF C.∠BED=∠CFD D.∠BDE =∠DAE
11. 如图,在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=4,CD=7,则AC的长为 ( )
A. 3 B. 11 C. 15 D. 9
12. 如图,ABC是一钢架的一部分,为使钢架更加坚固,在其内部添加了一些钢管DE,EF,FG…添加的这些钢管的长度都与BD的长度相等.如果∠ABC=10°,那么添加这样的钢管的根数最多是 ( )
A. 7 根 B. 8 根 C. 9 根 D. 10根
二、填空题(本大题共6 小题,每小题3分,共18分)
13. 命题“三角形的三个内角中至少有两个锐角”是 (填“真命题”或“假命题”).
14. 如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 .
15. 如图,以△ABC的顶点B为圆心,BA长为半径画弧,交 BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 度.
16. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是点D,
17. 如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 .
18. 在△ABC中,AB=AC,∠BAC=100°,点 D 在 BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的度数为 .
三、解答题(共54分)
19. (6分)如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点 C 不经过池塘可以直接到达点A 和B.连接AC 并延长到点 D,使 .连接BC并延长到点E,使 连接DE,那么量出DE的长就是A,B的距离.为什么
20. (8分)如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题
(2)你构造的命题是真命题还是假命题 若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
21. (8分)如图,已知等腰 顶角
(1)在AC上作一点D,使. (要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加墨).
(2)求证: 是等腰三角形.
22. (10分)如图,已知点 D,E分别是 的边 BA 和 BC 延长线上的点,作 的平分线 AF,若
(1)求证: 是等腰三角形.
(2)作. 的平分线交AF于点G,若 求 的度数.
23. (10分)在四边形ABCD中,对角线AC,BD相交于点E,且. 作 ,垂足为点 F, BF 与AC交于点 G,
(1)如图1,求证:
(2)如图2,BH是 的中线,若 ,在不添加任何辅助线的情况下,请直接写出图2 中四个三角形,使写出的每个三角形的面积都等于 面积的2倍.
24. (12 分)(1)小欣遇到这样一个问题:
如图1,在等边. 中, 于点 D,E为AB 上一点,BE的垂直平分线交AD 于点F,交AB于点G,连接EF,FC.求. 的度数.
小欣思考后发现,可以用两种方法解决问题:
方法一:通过运用线段垂直平分线性质定理和三角形内角和定理直接计算可解决问题.
方法二:过F作 于M,构造全等三角形可以解决问题.请你选择以上两种方法中的一种方法完成上述问题.
(2)参考小欣思考问题的方法,解决下列问题:
如图2,在等腰 中, 于点 D,E为BA延长线上一点,BE的垂直平分线交AD 于点F,交AB于点 G,连接EF,FC.猜想. 与 的数量关系,补全图形并加以证明.
专项练习(二)三角形
1. C 2. B 3. B 4. A 5. B 6. B 7. A 8. C 9. B 10. D11. B 12. B
13. 真命题 14. 9 15. 34 16. 1:3 17. 3 18. 130°或
19. 解:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),∴AB=DE.
∴DE的长就是A,B的距离.
20. 解:(1)可以构造3个命题,
命题①,如果AB∥CD,∠B=∠C,那么.
命题②,如果AB∥CD,∠E=∠F,那么.
命题③,如果∠E=∠F,∠B=∠C,那么.
(2)构造的3个命题都是真命题,证明命题①,
21. (1)解:如图,点 D 为所作.
(2)证明:∵ 72°,
∵ DA =DB,∴ ∠ABD=∠A =36°,
∴ ∠BDC =∠A +∠ABD=36°+36°=72°,∴∠BDC=∠C,∴△BCD是等腰三角形.
22. (1)证明:∵AF平分∠DAC,∴∠DAF=∠CAF,
∵AF∥BC,∴∠DAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,∴△ABC是等腰三角形.
(2)解:∵AB=AC,∠B=40°,
∴∠ACB=∠B=40°,∴∠BAC=100°,
∴∠ACE=∠BAC+∠B=140°,
∵ CG平分
∵AF∥BC,
∴∠AGC=180°-∠BCG=180°-40°-70°=70°.
23. 解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF,
∵AC⊥BD,BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF=90°,
∴∠DAE=∠GCF,
∴AD=CD.
(2)设DE=a,则AE=2DE=2a,EG=DE=a,
∵ BH是△ABE的中线,∴AH =HE=a,
∵AD=CD,AC⊥BD,∴CE=AE=2a,
则
在△ADE和△BGE中,
∴△ADE≌△BGE(ASA),∴BE=AE=2a,
,综上,面积等于△ADE面积的2倍的三角形有△ACD,
△ABE,△BCE,△BHG.
24. 解:(1)如图1,连接BF并延长交AC于点H,
∵ FG是BE的垂直平分线,∴FE=FB,
∴∠FEB=∠FBE,∴∠HFE=2∠FBE,
∵ △ABC为等边三角形,AD⊥BC,
∴ FD是BC的垂直平分线,∴FB=FC,
∴∠FBC=∠FCB,∴∠HFC=2∠FBC,
∴∠EFC=∠HFE+∠HFC=2(∠FBE+∠FBC)=2∠ABC=120°.
(2)补全图形如图2所示,连接BF,CE,
∵AB=AC,AD⊥BC,
∴∠ABC=∠ACB,BD=CD,
∴BF=CF,∴∠FBD=∠FCD,
∴∠FBE=∠FCA.又 FG垂直平分 BE,
∴FB=FE,∴∠FEB=∠FBE,∴∠FEB=∠FCA.
∵ ∠FEB + ∠AME + ∠MAE = 180°,∠FCA + ∠FMC +∠EFC=180°,∴∠EAC=∠EFC.∵BF=CF,FB=FE,
∴CF=EF,∴ ∠FEC=∠FCE.∵ ∠BAD+∠CAD+∠EAC=180°,∠FEC +∠FCE +∠EFC =180°,∠BAD =∠CAD,∴∠CAD=∠FCE.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题4分,共48分)
1. 在下列长度的三条线段中,不能组成三角形的是 ( )
A. 2cm ,3cm,4 cm B. 3cm,6cm,6cm C. 2cm,2cm,6 cm D. 5cm,6cm,7 cm
2. 下列命题中,是真命题的是 ( )
A. 等腰三角形的角平分线、中线和高重合
B. 若三角形有两个角相等,那么这两个角所对的边也相等
C. 等腰三角形任意两角都相等
D. 等腰三角形一定是锐角三角形
3. 如图,AD是△ABC的外角∠EAC 的平分线,AD∥BC,∠B=32°,则∠C 的度数是 ( )
A. 64° B. 32° C. 30° D. 40°
4. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是 ( )
A.∠A=∠D B. AC=DF C. AB=DE D. BF=EC
5. 如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是 ( )
A. 20° B. 35° C. 40° D. 70°
6. 三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为 ( )
A. 90° B. 60° C. 45° D. 30°
7. 通过如下尺规作图,能确定点D是边BC 中点的是 ( )
8. 如图,△ABC中,AC=BC
9. 如图,在△ABC中,AB边的中垂线DE 分别与AB边和AC边交于点 D 和点E,BC边的中垂线FG分别与BC边和AC边交于点 F和点G,又△BEG周长为16,且GE=1,则AC的长为 ( )
A. 13 B. 14 C. 15 D. 16
10. 如图,AD 是等腰△ABC 的顶角的平分线,点 E 在边 AB 上,点 F 在边 AC 上,且 AD 平分 ∠EDF,则下列结论错误的是 ( )
A. BE=CF B.∠BDE=∠CDF C.∠BED=∠CFD D.∠BDE =∠DAE
11. 如图,在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=4,CD=7,则AC的长为 ( )
A. 3 B. 11 C. 15 D. 9
12. 如图,ABC是一钢架的一部分,为使钢架更加坚固,在其内部添加了一些钢管DE,EF,FG…添加的这些钢管的长度都与BD的长度相等.如果∠ABC=10°,那么添加这样的钢管的根数最多是 ( )
A. 7 根 B. 8 根 C. 9 根 D. 10根
二、填空题(本大题共6 小题,每小题3分,共18分)
13. 命题“三角形的三个内角中至少有两个锐角”是 (填“真命题”或“假命题”).
14. 如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 .
15. 如图,以△ABC的顶点B为圆心,BA长为半径画弧,交 BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 度.
16. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是点D,
17. 如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 .
18. 在△ABC中,AB=AC,∠BAC=100°,点 D 在 BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的度数为 .
三、解答题(共54分)
19. (6分)如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点 C 不经过池塘可以直接到达点A 和B.连接AC 并延长到点 D,使 .连接BC并延长到点E,使 连接DE,那么量出DE的长就是A,B的距离.为什么
20. (8分)如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题
(2)你构造的命题是真命题还是假命题 若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
21. (8分)如图,已知等腰 顶角
(1)在AC上作一点D,使. (要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加墨).
(2)求证: 是等腰三角形.
22. (10分)如图,已知点 D,E分别是 的边 BA 和 BC 延长线上的点,作 的平分线 AF,若
(1)求证: 是等腰三角形.
(2)作. 的平分线交AF于点G,若 求 的度数.
23. (10分)在四边形ABCD中,对角线AC,BD相交于点E,且. 作 ,垂足为点 F, BF 与AC交于点 G,
(1)如图1,求证:
(2)如图2,BH是 的中线,若 ,在不添加任何辅助线的情况下,请直接写出图2 中四个三角形,使写出的每个三角形的面积都等于 面积的2倍.
24. (12 分)(1)小欣遇到这样一个问题:
如图1,在等边. 中, 于点 D,E为AB 上一点,BE的垂直平分线交AD 于点F,交AB于点G,连接EF,FC.求. 的度数.
小欣思考后发现,可以用两种方法解决问题:
方法一:通过运用线段垂直平分线性质定理和三角形内角和定理直接计算可解决问题.
方法二:过F作 于M,构造全等三角形可以解决问题.请你选择以上两种方法中的一种方法完成上述问题.
(2)参考小欣思考问题的方法,解决下列问题:
如图2,在等腰 中, 于点 D,E为BA延长线上一点,BE的垂直平分线交AD 于点F,交AB于点 G,连接EF,FC.猜想. 与 的数量关系,补全图形并加以证明.
专项练习(二)三角形
1. C 2. B 3. B 4. A 5. B 6. B 7. A 8. C 9. B 10. D11. B 12. B
13. 真命题 14. 9 15. 34 16. 1:3 17. 3 18. 130°或
19. 解:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),∴AB=DE.
∴DE的长就是A,B的距离.
20. 解:(1)可以构造3个命题,
命题①,如果AB∥CD,∠B=∠C,那么.
命题②,如果AB∥CD,∠E=∠F,那么.
命题③,如果∠E=∠F,∠B=∠C,那么.
(2)构造的3个命题都是真命题,证明命题①,
21. (1)解:如图,点 D 为所作.
(2)证明:∵ 72°,
∵ DA =DB,∴ ∠ABD=∠A =36°,
∴ ∠BDC =∠A +∠ABD=36°+36°=72°,∴∠BDC=∠C,∴△BCD是等腰三角形.
22. (1)证明:∵AF平分∠DAC,∴∠DAF=∠CAF,
∵AF∥BC,∴∠DAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,∴△ABC是等腰三角形.
(2)解:∵AB=AC,∠B=40°,
∴∠ACB=∠B=40°,∴∠BAC=100°,
∴∠ACE=∠BAC+∠B=140°,
∵ CG平分
∵AF∥BC,
∴∠AGC=180°-∠BCG=180°-40°-70°=70°.
23. 解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF,
∵AC⊥BD,BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF=90°,
∴∠DAE=∠GCF,
∴AD=CD.
(2)设DE=a,则AE=2DE=2a,EG=DE=a,
∵ BH是△ABE的中线,∴AH =HE=a,
∵AD=CD,AC⊥BD,∴CE=AE=2a,
则
在△ADE和△BGE中,
∴△ADE≌△BGE(ASA),∴BE=AE=2a,
,综上,面积等于△ADE面积的2倍的三角形有△ACD,
△ABE,△BCE,△BHG.
24. 解:(1)如图1,连接BF并延长交AC于点H,
∵ FG是BE的垂直平分线,∴FE=FB,
∴∠FEB=∠FBE,∴∠HFE=2∠FBE,
∵ △ABC为等边三角形,AD⊥BC,
∴ FD是BC的垂直平分线,∴FB=FC,
∴∠FBC=∠FCB,∴∠HFC=2∠FBC,
∴∠EFC=∠HFE+∠HFC=2(∠FBE+∠FBC)=2∠ABC=120°.
(2)补全图形如图2所示,连接BF,CE,
∵AB=AC,AD⊥BC,
∴∠ABC=∠ACB,BD=CD,
∴BF=CF,∴∠FBD=∠FCD,
∴∠FBE=∠FCA.又 FG垂直平分 BE,
∴FB=FE,∴∠FEB=∠FBE,∴∠FEB=∠FCA.
∵ ∠FEB + ∠AME + ∠MAE = 180°,∠FCA + ∠FMC +∠EFC=180°,∴∠EAC=∠EFC.∵BF=CF,FB=FE,
∴CF=EF,∴ ∠FEC=∠FCE.∵ ∠BAD+∠CAD+∠EAC=180°,∠FEC +∠FCE +∠EFC =180°,∠BAD =∠CAD,∴∠CAD=∠FCE.
同课章节目录
