物理人教版(2019)选择性必修第一册2.2简谐运动的描述(共18张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.2简谐运动的描述(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-16 09:15:36 | ||
图片预览




文档简介
(共18张PPT)
人教版物理选择性必修一第二章《机械振动》
第二节 简谐运动的描述
回顾与复习:
1.在高中物理必修一课本中我们曾经用哪些物理量来描述匀变速直线运动?
2.在高中物理必修二课本中我们曾经用哪些物理量来描述匀速圆周运动?
对于简谐运动,我们该用哪些物理量来描述呢?
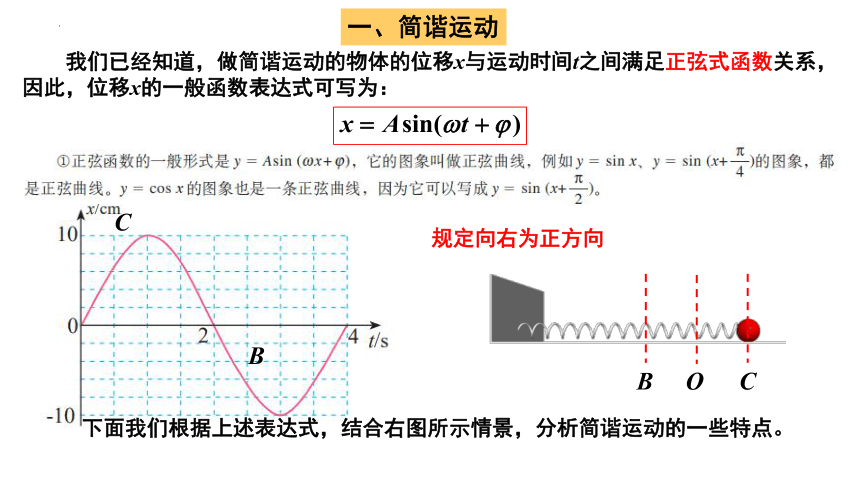
一、简谐运动
下面我们根据上述表达式,结合右图所示情景,分析简谐运动的一些特点。
B
C
C
B
O
规定向右为正方向
我们已经知道,做简谐运动的物体的位移x与运动时间t之间满足正弦式函数关系,因此,位移x的一般函数表达式可写为:
一、简谐运动
描述简谐运动的物理量
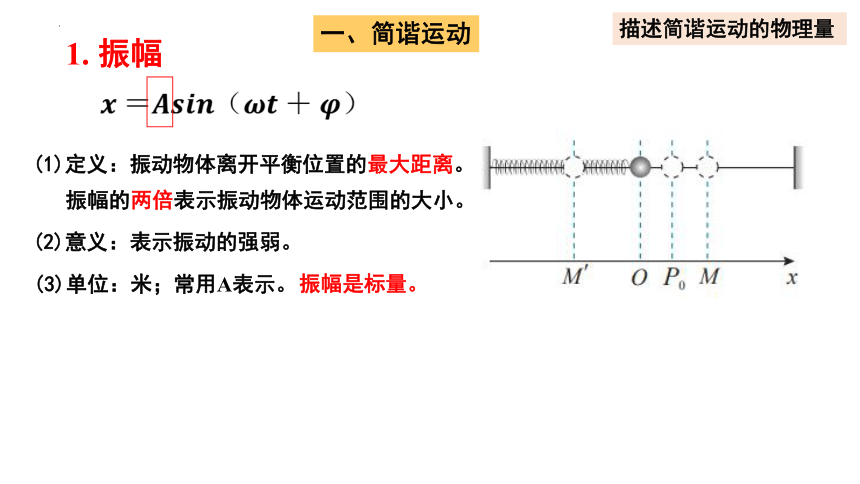
1. 振幅
(1)定义:振动物体离开平衡位置的最大距离。
振幅的两倍表示振动物体运动范围的大小。
(2)意义:表示振动的强弱。
(3)单位:米;常用A表示。
振幅是标量。
简谐运动中的振幅、位移和路程
振幅 位移 路程
意义
矢量标量
变化
联系 振动物体离开平衡位的
最大距离
从平衡位置指向振子所在位置的有向线段
运动轨迹的长度
标量
矢量
标量
不发生变化
大小和方向随时间做周期性变化
随时间增加
振幅等于位移最大值的数值。
二、周期和频率
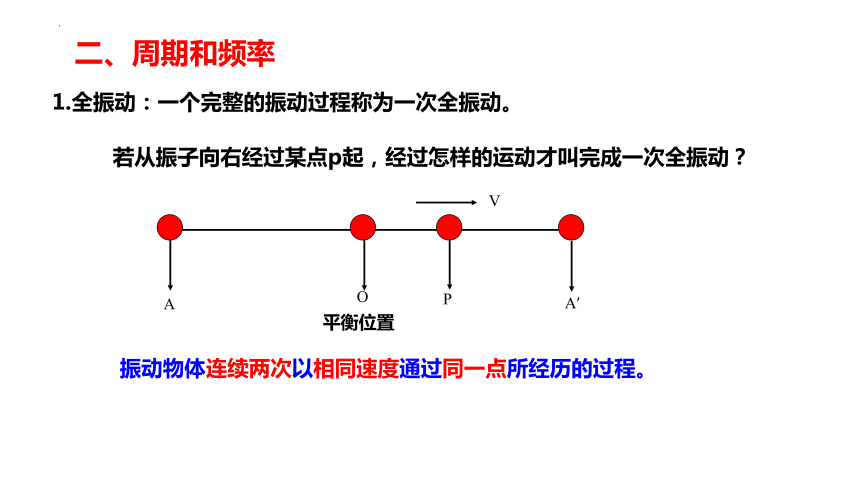
1.全振动:一个完整的振动过程称为一次全振动。
若从振子向右经过某点p起,经过怎样的运动才叫完成一次全振动?
O
A
P
V
平衡位置
A′
振动物体连续两次以相同速度通过同一点所经历的过程。
2.周期:做简谐运动的物体完成一次全振动所需要的时间,称为周期T,单位:s。
二、周期和频率
3.频率:物体完成全振动的次数与所用时间之比叫作频率f,数值等于单位时间内完成的全振动的次数。单位:赫兹(Hz)。1Hz=1s-1。
5.周期和频率的关系:T=1/f。
4.意义:周期和频率都是表示物体振动快慢的物理量,周期越小,频率越大, 表示振动越快。
二、周期和频率
思考与讨论:
对于正弦函数x=Asin(ωt+φ),要使函数值循环变化一次,(ωt+φ)需要增加多少?这一变化过程所需的时间为多少?
于是有:[ω(t+T)+φ]-(ωt+φ)=2π
由此解出:
根据周期与频率的关系,则:ω=2πf
5. ω是一个与周期成反比,与频率成正比的量,叫作简谐运动的“圆频率”。它也表示简谐运动的快慢。
实验:测量小球振动的周期
2.弹簧振子周期和频率由振动系统本身的因素决定。
1.振动周期与振幅大小无关;
实验结论:
拓展:弹簧振子周期公式
思考与讨论:
1.根据正弦函数x=Asin(ωt+φ),当(ωt+φ)确定时,sin(ωt+φ)的值是否确定呢?
2.你认为在物体所做的简谐运动中,(ωt+φ)代表的物理意义是什么?
三、相位
1.定义:物理学中把(ωt+φ)叫作相位。其中φ是t=0时的相位,称作初相位或初相。
2.意义:是表示物体振动步调的物理量,用相位来描述简谐运动在各个时刻所处的不同状态。
3.相位差:实际上经常用到的是两个相同频率的简谐运动的相位差,简称相差。
实验:观察两个小球的振动情况
思考与讨论:
1.若做简谐运动的两个物体,步调始终一致,需要满足什么条件?
同相:相位差为零,一般地为 =2n (n=0,1,2,……)
2.若做简谐运动的两个物体,步调始终相反,需要满足什么条件?
反相:相位差为 ,一般地为 =(2n+1) (n=0,1,2,……)
以x代表质点对于平衡位置的位移,t 代表时间,则:
振幅
圆频率
初相位
四、简谐运动的表达式
相位
【例1】如图 ,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
人教版物理选择性必修一第二章《机械振动》
第二节 简谐运动的描述
回顾与复习:
1.在高中物理必修一课本中我们曾经用哪些物理量来描述匀变速直线运动?
2.在高中物理必修二课本中我们曾经用哪些物理量来描述匀速圆周运动?
对于简谐运动,我们该用哪些物理量来描述呢?
一、简谐运动
下面我们根据上述表达式,结合右图所示情景,分析简谐运动的一些特点。
B
C
C
B
O
规定向右为正方向
我们已经知道,做简谐运动的物体的位移x与运动时间t之间满足正弦式函数关系,因此,位移x的一般函数表达式可写为:
一、简谐运动
描述简谐运动的物理量
1. 振幅
(1)定义:振动物体离开平衡位置的最大距离。
振幅的两倍表示振动物体运动范围的大小。
(2)意义:表示振动的强弱。
(3)单位:米;常用A表示。
振幅是标量。
简谐运动中的振幅、位移和路程
振幅 位移 路程
意义
矢量标量
变化
联系 振动物体离开平衡位的
最大距离
从平衡位置指向振子所在位置的有向线段
运动轨迹的长度
标量
矢量
标量
不发生变化
大小和方向随时间做周期性变化
随时间增加
振幅等于位移最大值的数值。
二、周期和频率
1.全振动:一个完整的振动过程称为一次全振动。
若从振子向右经过某点p起,经过怎样的运动才叫完成一次全振动?
O
A
P
V
平衡位置
A′
振动物体连续两次以相同速度通过同一点所经历的过程。
2.周期:做简谐运动的物体完成一次全振动所需要的时间,称为周期T,单位:s。
二、周期和频率
3.频率:物体完成全振动的次数与所用时间之比叫作频率f,数值等于单位时间内完成的全振动的次数。单位:赫兹(Hz)。1Hz=1s-1。
5.周期和频率的关系:T=1/f。
4.意义:周期和频率都是表示物体振动快慢的物理量,周期越小,频率越大, 表示振动越快。
二、周期和频率
思考与讨论:
对于正弦函数x=Asin(ωt+φ),要使函数值循环变化一次,(ωt+φ)需要增加多少?这一变化过程所需的时间为多少?
于是有:[ω(t+T)+φ]-(ωt+φ)=2π
由此解出:
根据周期与频率的关系,则:ω=2πf
5. ω是一个与周期成反比,与频率成正比的量,叫作简谐运动的“圆频率”。它也表示简谐运动的快慢。
实验:测量小球振动的周期
2.弹簧振子周期和频率由振动系统本身的因素决定。
1.振动周期与振幅大小无关;
实验结论:
拓展:弹簧振子周期公式
思考与讨论:
1.根据正弦函数x=Asin(ωt+φ),当(ωt+φ)确定时,sin(ωt+φ)的值是否确定呢?
2.你认为在物体所做的简谐运动中,(ωt+φ)代表的物理意义是什么?
三、相位
1.定义:物理学中把(ωt+φ)叫作相位。其中φ是t=0时的相位,称作初相位或初相。
2.意义:是表示物体振动步调的物理量,用相位来描述简谐运动在各个时刻所处的不同状态。
3.相位差:实际上经常用到的是两个相同频率的简谐运动的相位差,简称相差。
实验:观察两个小球的振动情况
思考与讨论:
1.若做简谐运动的两个物体,步调始终一致,需要满足什么条件?
同相:相位差为零,一般地为 =2n (n=0,1,2,……)
2.若做简谐运动的两个物体,步调始终相反,需要满足什么条件?
反相:相位差为 ,一般地为 =(2n+1) (n=0,1,2,……)
以x代表质点对于平衡位置的位移,t 代表时间,则:
振幅
圆频率
初相位
四、简谐运动的表达式
相位
【例1】如图 ,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
