人教版数学九年级上册第二十四章圆单元试卷(含答案)
文档属性
| 名称 | 人教版数学九年级上册第二十四章圆单元试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 459.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 14:21:16 | ||
图片预览



文档简介
人教版数学九年级上册 第二十四章圆 单元试卷
一、单选题
1.一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.180° C.240° D.300°
2.以点为圆心画,若的半径,则与轴的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
3.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是( )
A.2 B. C. D.1
4.如图,四边形内接于,若,则( )
A. B. C. D.
5.如图,四边形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O与CD相切于E,与BC相交于F,若AB=8,AD=2,则图中两阴影部分面积之和为( )
A. B. C.3 D.
6.如图,内接于,,则等于( )
A. B. C. D.
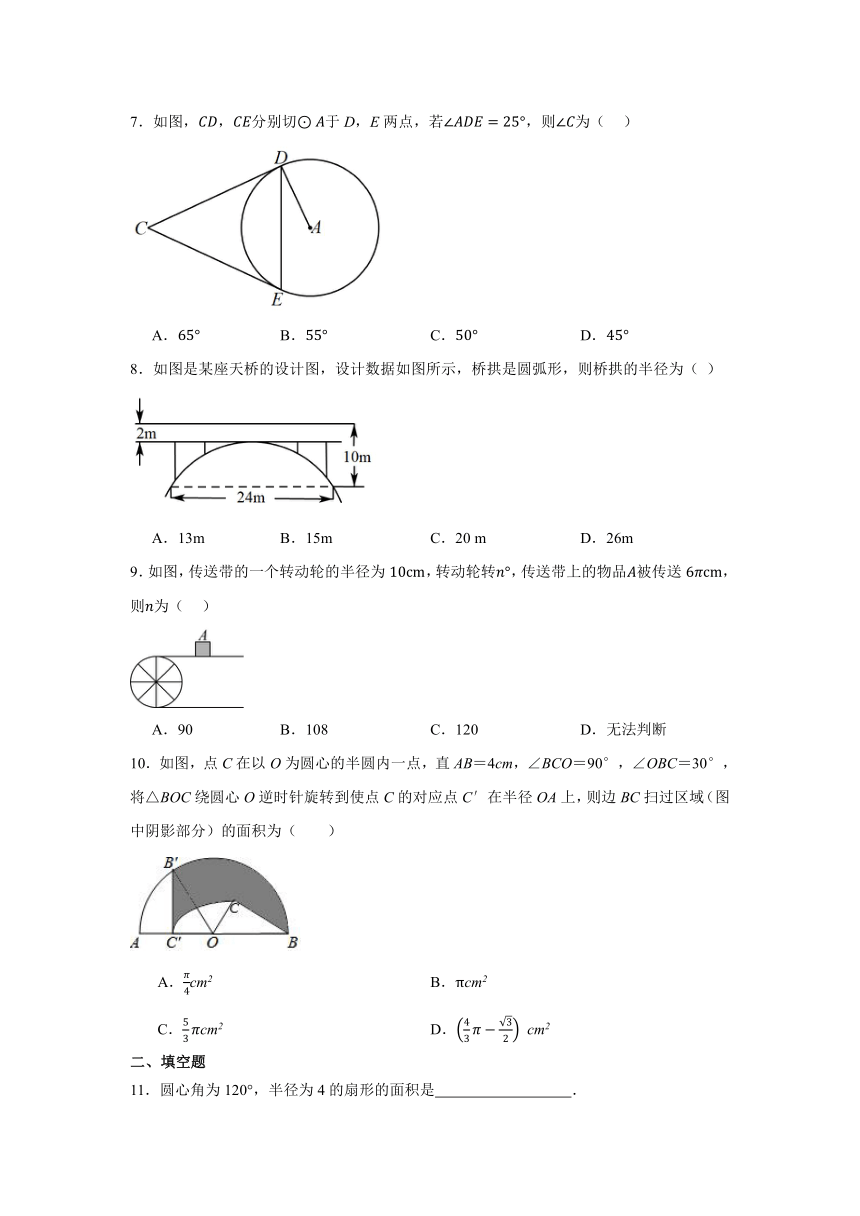
7.如图,,分别切于D,E两点,若,则为( )
A. B. C. D.
8.如图是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
A.13m B.15m C.20 m D.26m
9.如图,传送带的一个转动轮的半径为,转动轮转,传送带上的物品被传送,则为( )
A.90 B.108 C.120 D.无法判断
10.如图,点C在以O为圆心的半圆内一点,直AB=4cm,∠BCO=90°,∠OBC=30°,将△BOC绕圆心O逆时针旋转到使点C的对应点C′在半径OA上,则边BC扫过区域(图中阴影部分)的面积为( )
A.cm2 B.πcm2
C.cm2 D. cm2
二、填空题
11.圆心角为120°,半径为4的扇形的面积是 .
12.边长为,,的三角形,其内心和外心间的距离为 .
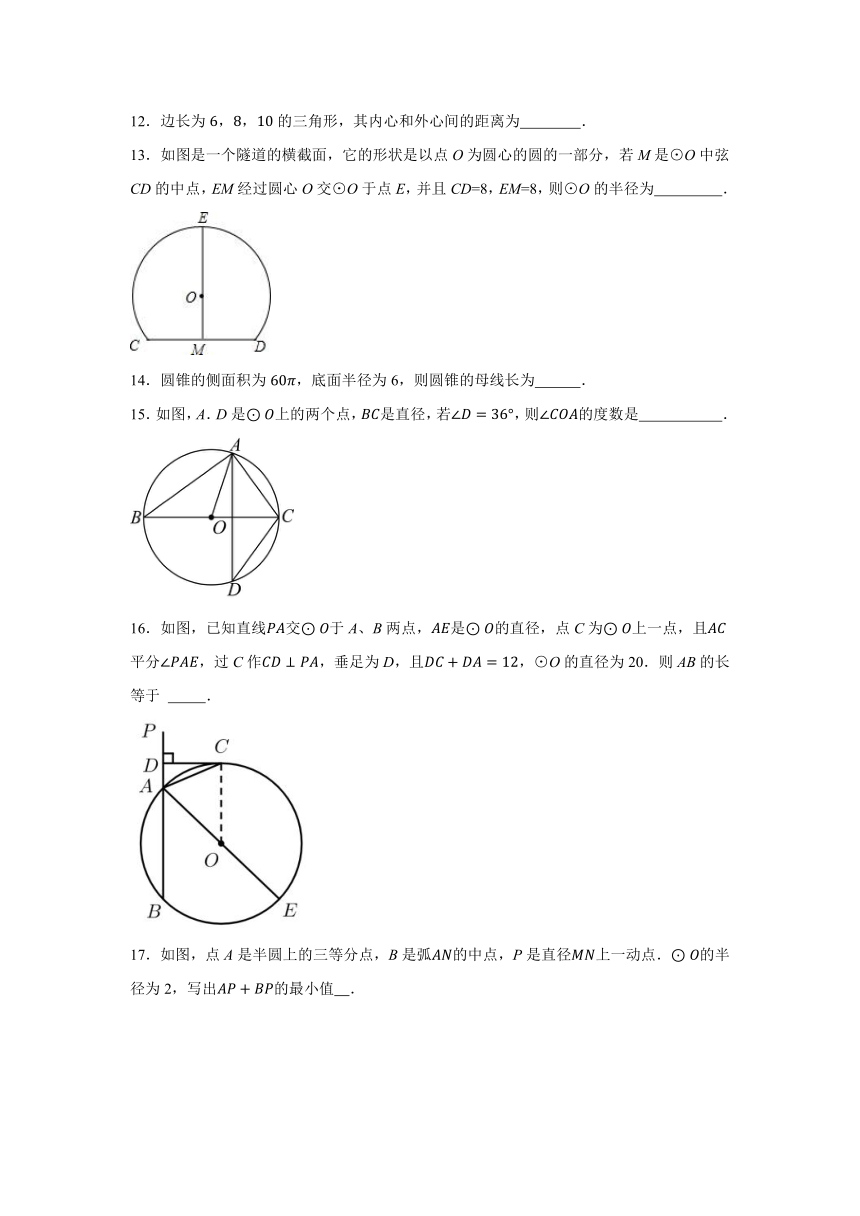
13.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,若M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=8,EM=8,则⊙O的半径为 .
14.圆锥的侧面积为,底面半径为6,则圆锥的母线长为 .
15.如图,A.D是上的两个点,是直径,若,则的度数是 .
16.如图,已知直线交于A、B两点,是的直径,点C为上一点,且平分,过C作,垂足为D,且,⊙O的直径为20.则AB的长等于 .
17.如图,点A是半圆上的三等分点,B是弧的中点,P是直径上一动点.的半径为2,写出的最小值 .
三、解答题
18.如图,的半径为1,点A,B,C是上的三个点,点P在劣弧上,,平分.求证:
(1)是等边三角形;
(2).
19.如图,AB是的直径,弦的平分线交于点D,过点D作交CA的延长线于点E,连接AD,BD.
(1)求证:DE是的切线;
(2)求AB的长.
20.如图,是的一条弦,,垂足为点,交于点,点在上.
(1)若,求的度数;
(2)若,,求的长.
21.如图,在中,点为的中点,弦、互相垂直,垂足为,分别与、相交于点、,连接、.
(1)求证:为的中点.
(2)若的半径为,的度数为,求线段的长.
22.如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为的中点.
(1)求证:AB=BC;
(2)试判断四边形BOCD的形状,并说明理由.
23.如图1,在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A出发沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上).设点D移动的时间为t秒.
(1)试判断四边形DFCE的形状,并说明理由;
(2)当t为何值时,四边形DFCE的面积等于20cm2?
(3)如图2,以点F为圆心,FC的长为半径作⊙F,在运动过程中,当⊙F与四边形DFCE只有1个公共点时,请直接写出t的取值范围.
24.在平面直角坐标系中,点,,若,且A,均不为原点,则称A和互为正交点.比如:,,其中,那么和互为正交点.
(1)点A和互为正交点,A的坐标为.
①如果的坐标为,那么的值为;
②如果的坐标为,求与之间的关系式;
(2)如图,点A和互为正交点,求出的度数;
(3)点A,是以为圆心,半径为的圆上的正交点,以线段为边,构造正方形,原点在正方形的外部,请直接写出线段长度的取值范围.
参考答案:
1.A
2.A
3.A
4.C
5.A
6.C
7.C
8.A
9.B
10.B
11.π
12.
13.5
14.10
15.
16.12
17.
18.(1)证明:∵,平分,
∴,
∵,
∴,
∴,
∴是等边三角形;
(2)证明:在上截取,
∵,
∴为等边三角形,
∴,,
由(1)知为等边三角形,
∴,,
∴,
∴,
∴,
∴.
19.(1)如图,连接,
∵AB为直径,CD平分∠ACB
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∵DE∥AB,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)如图,过点作
∠ACD=45°,
在中,
在中,
20.(1)解:∵是的一条弦,,
∴,
又∵,
∴.
(2)解:∵,
∴,
在中,,
∵是的一条弦,,
∴,
则.
21.(1)∵点为的中点
∴
∴
∵
∴
∴
∵
∴°
在和中
∴
∴
∴点N为BE中点
(2)连接CA,AB,OA,OB,如图所示:
∵点为的中点
∴
在和中
∴
∴,即M为AE中点
∵N为BE中点
∴MN为的中位线
又∵的半径为,的度数为
∴,OA=OB=8
∴
∴
22.解:(1)证明:∵AB是⊙O的切线,
∴∠OBA=90°,∠AOB=90°-30°=60°.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠AOB=30°=∠A,
∴AB=BC.
(2)四边形BOCD为菱形.
理由如下:连接OD交BC于点M.
∵D是弧BC中点
∴OD垂直平分BC.
在Rt△OMC中,
∵∠OCM=30°,
∴OC=2OM=OD,
∴OM=MD,
∴四边形BOCD为菱形.
23.解:(1)∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形;
(2)如图1中,设点D出发t秒后四边形DFCE的面积为20cm2,根据题意得,
DE=AD=2t,BD=12﹣2t,CF=DE=2t,
又∵BD×CF=四边形DFCE的面积,
∴2t(12﹣2t)=20,
t2﹣6t+5=0,
(t﹣1)(t﹣5)=0,
解得t1=1,t2=5;
答:点D出发1秒或5秒后四边形DFCE的面积为20cm2;
(3)如图2中,当点D在⊙F上时,⊙F与四边形DECF有两个公共点,
在Rt△DFB中,∵∠B=90°,AD=DF=CF=2t,BD=BF=12﹣2t,
∴2t=(12﹣2t),
∴t=12﹣6,
由图象可知,当12﹣6<t<6时,⊙F与四边形DFCE有1个公共点.
24.(1)解:①∵A和互为正交点,A的坐标为,的坐标为,
∴,
解得:;
②由题意得:,
与之间的关系式为.
(2)解:设,.
,,
点A和互为正交点,
,
∴,
.
(3)解:如图,连接
由题意得:,
∴是圆的直径,,
∴,
在中,,
∴当O、K、C三点共线时,的值最大,最大值为,
∵原点在正方形的外部,
∴当点C在x轴上时,的值最小,最小值为4,
∴线段长度的取值范围为:.
一、单选题
1.一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.180° C.240° D.300°
2.以点为圆心画,若的半径,则与轴的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
3.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是( )
A.2 B. C. D.1
4.如图,四边形内接于,若,则( )
A. B. C. D.
5.如图,四边形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O与CD相切于E,与BC相交于F,若AB=8,AD=2,则图中两阴影部分面积之和为( )
A. B. C.3 D.
6.如图,内接于,,则等于( )
A. B. C. D.
7.如图,,分别切于D,E两点,若,则为( )
A. B. C. D.
8.如图是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
A.13m B.15m C.20 m D.26m
9.如图,传送带的一个转动轮的半径为,转动轮转,传送带上的物品被传送,则为( )
A.90 B.108 C.120 D.无法判断
10.如图,点C在以O为圆心的半圆内一点,直AB=4cm,∠BCO=90°,∠OBC=30°,将△BOC绕圆心O逆时针旋转到使点C的对应点C′在半径OA上,则边BC扫过区域(图中阴影部分)的面积为( )
A.cm2 B.πcm2
C.cm2 D. cm2
二、填空题
11.圆心角为120°,半径为4的扇形的面积是 .
12.边长为,,的三角形,其内心和外心间的距离为 .
13.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,若M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=8,EM=8,则⊙O的半径为 .
14.圆锥的侧面积为,底面半径为6,则圆锥的母线长为 .
15.如图,A.D是上的两个点,是直径,若,则的度数是 .
16.如图,已知直线交于A、B两点,是的直径,点C为上一点,且平分,过C作,垂足为D,且,⊙O的直径为20.则AB的长等于 .
17.如图,点A是半圆上的三等分点,B是弧的中点,P是直径上一动点.的半径为2,写出的最小值 .
三、解答题
18.如图,的半径为1,点A,B,C是上的三个点,点P在劣弧上,,平分.求证:
(1)是等边三角形;
(2).
19.如图,AB是的直径,弦的平分线交于点D,过点D作交CA的延长线于点E,连接AD,BD.
(1)求证:DE是的切线;
(2)求AB的长.
20.如图,是的一条弦,,垂足为点,交于点,点在上.
(1)若,求的度数;
(2)若,,求的长.
21.如图,在中,点为的中点,弦、互相垂直,垂足为,分别与、相交于点、,连接、.
(1)求证:为的中点.
(2)若的半径为,的度数为,求线段的长.
22.如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为的中点.
(1)求证:AB=BC;
(2)试判断四边形BOCD的形状,并说明理由.
23.如图1,在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A出发沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上).设点D移动的时间为t秒.
(1)试判断四边形DFCE的形状,并说明理由;
(2)当t为何值时,四边形DFCE的面积等于20cm2?
(3)如图2,以点F为圆心,FC的长为半径作⊙F,在运动过程中,当⊙F与四边形DFCE只有1个公共点时,请直接写出t的取值范围.
24.在平面直角坐标系中,点,,若,且A,均不为原点,则称A和互为正交点.比如:,,其中,那么和互为正交点.
(1)点A和互为正交点,A的坐标为.
①如果的坐标为,那么的值为;
②如果的坐标为,求与之间的关系式;
(2)如图,点A和互为正交点,求出的度数;
(3)点A,是以为圆心,半径为的圆上的正交点,以线段为边,构造正方形,原点在正方形的外部,请直接写出线段长度的取值范围.
参考答案:
1.A
2.A
3.A
4.C
5.A
6.C
7.C
8.A
9.B
10.B
11.π
12.
13.5
14.10
15.
16.12
17.
18.(1)证明:∵,平分,
∴,
∵,
∴,
∴,
∴是等边三角形;
(2)证明:在上截取,
∵,
∴为等边三角形,
∴,,
由(1)知为等边三角形,
∴,,
∴,
∴,
∴,
∴.
19.(1)如图,连接,
∵AB为直径,CD平分∠ACB
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∵DE∥AB,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)如图,过点作
∠ACD=45°,
在中,
在中,
20.(1)解:∵是的一条弦,,
∴,
又∵,
∴.
(2)解:∵,
∴,
在中,,
∵是的一条弦,,
∴,
则.
21.(1)∵点为的中点
∴
∴
∵
∴
∴
∵
∴°
在和中
∴
∴
∴点N为BE中点
(2)连接CA,AB,OA,OB,如图所示:
∵点为的中点
∴
在和中
∴
∴,即M为AE中点
∵N为BE中点
∴MN为的中位线
又∵的半径为,的度数为
∴,OA=OB=8
∴
∴
22.解:(1)证明:∵AB是⊙O的切线,
∴∠OBA=90°,∠AOB=90°-30°=60°.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠AOB=30°=∠A,
∴AB=BC.
(2)四边形BOCD为菱形.
理由如下:连接OD交BC于点M.
∵D是弧BC中点
∴OD垂直平分BC.
在Rt△OMC中,
∵∠OCM=30°,
∴OC=2OM=OD,
∴OM=MD,
∴四边形BOCD为菱形.
23.解:(1)∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形;
(2)如图1中,设点D出发t秒后四边形DFCE的面积为20cm2,根据题意得,
DE=AD=2t,BD=12﹣2t,CF=DE=2t,
又∵BD×CF=四边形DFCE的面积,
∴2t(12﹣2t)=20,
t2﹣6t+5=0,
(t﹣1)(t﹣5)=0,
解得t1=1,t2=5;
答:点D出发1秒或5秒后四边形DFCE的面积为20cm2;
(3)如图2中,当点D在⊙F上时,⊙F与四边形DECF有两个公共点,
在Rt△DFB中,∵∠B=90°,AD=DF=CF=2t,BD=BF=12﹣2t,
∴2t=(12﹣2t),
∴t=12﹣6,
由图象可知,当12﹣6<t<6时,⊙F与四边形DFCE有1个公共点.
24.(1)解:①∵A和互为正交点,A的坐标为,的坐标为,
∴,
解得:;
②由题意得:,
与之间的关系式为.
(2)解:设,.
,,
点A和互为正交点,
,
∴,
.
(3)解:如图,连接
由题意得:,
∴是圆的直径,,
∴,
在中,,
∴当O、K、C三点共线时,的值最大,最大值为,
∵原点在正方形的外部,
∴当点C在x轴上时,的值最小,最小值为4,
∴线段长度的取值范围为:.
同课章节目录
