第十一章 三角形 单元练习(含答案) 2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 单元练习(含答案) 2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 521.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-16 22:16:48 | ||
图片预览


文档简介
第十一章 三角形 单元练习 2024-2025学年人教版数学八年级上册
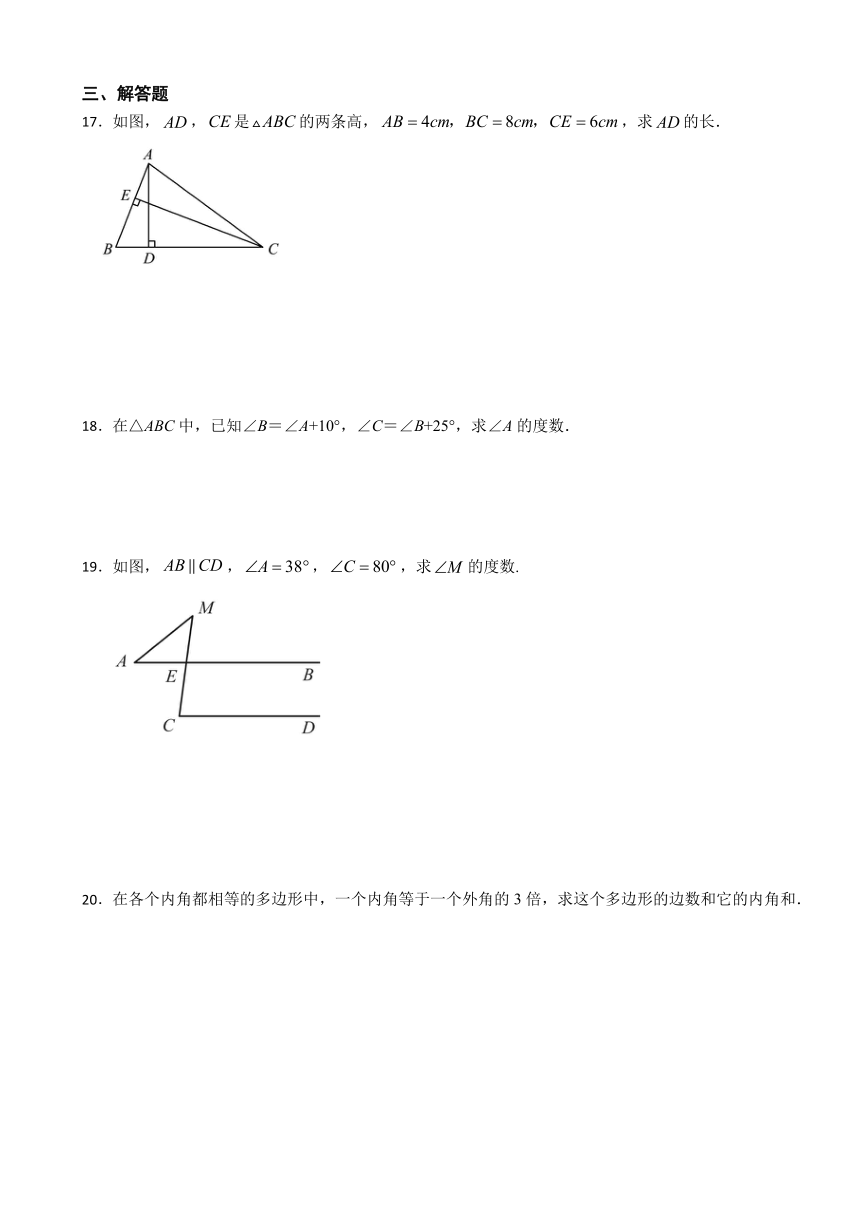
一、单选题
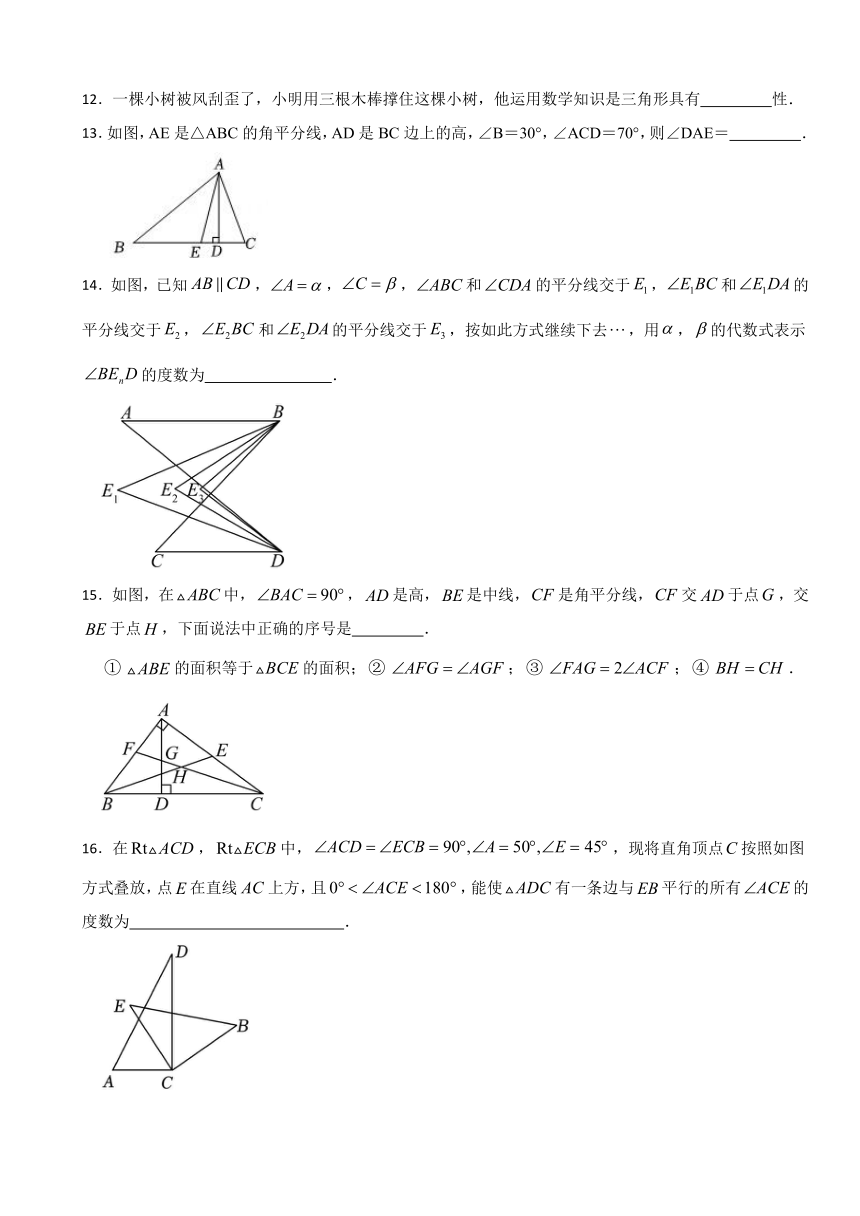
1.下列四个图中,正确画出中边上的高是( )
A. B.
C. D.
2.如图,一棵树生长在的山坡上,树干垂直于水平线,则的度数为( )
A. B. C. D.
3.已知三角形的两条边长分别为和,则其第三边长可能为( )
A. B. C. D.
4.将一个三角尺按如图所示的方式放置,∠ACB=90°,∠ABC=60°,点B,C分别在直线PQ,MN 上.若 PQ∥MN,∠ACM=44°,则∠PBC的度数为( )
A.46° B.44° C.22° D.20°
5.如图,中,是边上的中线,,,那么和的周长的差是( )
A. B. C. D.
6.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.DE是△ABC的中线
7.如图,△ABC的中线AD、BE相交于点F.若△ABF的面积是4,则四边形FDCE的面积是( )
A.4 B.4.5 C.3.5 D.5
8.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值( )
A.7 B.8 C.14 D.15
二、填空题
9.正十二边形的外角和为 .
10.设a,b,c为△ABC的三边,化简|a﹣b+c|﹣|a+b﹣c|﹣|a﹣b﹣c|= .
11.如图,三角形ABC的面积为1,BD:DC=1:3,E是AC的中点,AD与BE相交于点P,那么四边形EPDC的面积为 .
12.一棵小树被风刮歪了,小明用三根木棒撑住这棵小树,他运用数学知识是三角形具有 性.
13.如图,AE是△ABC的角平分线,AD是BC边上的高,∠B=30°,∠ACD=70°,则∠DAE= .
14.如图,已知,,,和的平分线交于,和的平分线交于,和的平分线交于,按如此方式继续下去,用,的代数式表示的度数为 .
15.如图,在中,,是高,是中线,是角平分线,交于点,交于点,下面说法中正确的序号是 .
的面积等于的面积;;;.
16.在,中,,现将直角顶点按照如图方式叠放,点在直线上方,且,能使有一条边与平行的所有的度数为 .
三、解答题
17.如图,,是的两条高,,求的长.
18.在△ABC中,已知∠B=∠A+10°,∠C=∠B+25°,求∠A的度数.
19.如图,,,,求的度数.
20.在各个内角都相等的多边形中,一个内角等于一个外角的3倍,求这个多边形的边数和它的内角和.
21. 如图,将△ABC向左平移6个单位长度,再向下平移4个单位长度,可以得到△A1B1C1,画出平移后的△A1B1C1
①直接写出△A1B1C1各个顶点的坐标;
②写出S△ABC= ▲ .
22.如图,△ABC中,∠ABC的角平分线与外角∠ACD的平分线交于A1.
(1)如图1,若∠A=70°,则∠A1= .
(2)如图2,四边形ABCD中,∠ABC的角平分线及外角∠DCE的角平分线相交于点F, 若∠A+∠D=230°, 求∠F的度数.
(3)如图3,△ABC中,∠ABC的角平分线与外角∠ACD的角平分线交于A1,若E为BA延长线上一动点,连接EC,∠AEC与∠ACE的角平分线交于点Q ,当E滑动时有下面两个结论:
①∠Q+∠A1的值为定值;
②∠Q-∠A1的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】A
8.【答案】C
9.【答案】360°
10.【答案】a﹣3b+c
11.【答案】
12.【答案】稳定
13.【答案】20°
14.【答案】
15.【答案】
16.【答案】或或
17.【答案】
18.【答案】解:∵∠B=∠A+10°,∠C=∠B+25°,
∴∠C=∠B+25° ,
∵
∴
解得
19.【答案】解:∵,,
∴,
∵,,
∴
20.【答案】解:∵在这个正多边形中,一个内角等于与它相邻的一个外角的3倍,则可设这个内角为x则与它相邻的外角度数为:,
由题意可知:,
解得x=135°,
则与它相邻的外角度数为 45°,
∵360°÷45°=8,
∴这个多边形的边数为8,其内角和为8×135°=1080°.
21.【答案】解:①A(-2,1)B(-3,-3)C(-5,-2);
②
22.【答案】(1)35°
(2)解:如图:
∵BF平分∠ABC,CF平分∠DCE,
∴∠FBC=∠ABC,∠FCE=∠DCE
∴∠F=∠FCE-∠FBC=(∠DCE-∠ABC),
∵∠A+∠D=230°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=130°,
∴∠ABC+(180°-∠DCE)=130°,
∴∠DCE-∠ABC=50°,
∴∠F=(∠DCE-∠ABC)=25°;
(3)解:正确的结论是①,理由如下:
如图:
同(1)可得∠A1=∠BAC,
∵EQ平分∠AEC,CQ平分∠ACE,
∴∠QEC=∠AEC,∠QCE=∠ACE,
∵∠Q=180°-(∠QEC+∠QCE),
∴∠Q=180°-(∠AEC+∠ACE),
∵∠BAC=∠AEC+∠ACE,
∴∠Q=180°-∠BAC,
而∠A1=∠BAC,
∴∠Q+∠A1=180°-∠BAC+∠BAC=180°,
∴∠Q+∠A1的值为定值,①正确,其值是180°.
一、单选题
1.下列四个图中,正确画出中边上的高是( )
A. B.
C. D.
2.如图,一棵树生长在的山坡上,树干垂直于水平线,则的度数为( )
A. B. C. D.
3.已知三角形的两条边长分别为和,则其第三边长可能为( )
A. B. C. D.
4.将一个三角尺按如图所示的方式放置,∠ACB=90°,∠ABC=60°,点B,C分别在直线PQ,MN 上.若 PQ∥MN,∠ACM=44°,则∠PBC的度数为( )
A.46° B.44° C.22° D.20°
5.如图,中,是边上的中线,,,那么和的周长的差是( )
A. B. C. D.
6.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.DE是△ABC的中线
7.如图,△ABC的中线AD、BE相交于点F.若△ABF的面积是4,则四边形FDCE的面积是( )
A.4 B.4.5 C.3.5 D.5
8.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值( )
A.7 B.8 C.14 D.15
二、填空题
9.正十二边形的外角和为 .
10.设a,b,c为△ABC的三边,化简|a﹣b+c|﹣|a+b﹣c|﹣|a﹣b﹣c|= .
11.如图,三角形ABC的面积为1,BD:DC=1:3,E是AC的中点,AD与BE相交于点P,那么四边形EPDC的面积为 .
12.一棵小树被风刮歪了,小明用三根木棒撑住这棵小树,他运用数学知识是三角形具有 性.
13.如图,AE是△ABC的角平分线,AD是BC边上的高,∠B=30°,∠ACD=70°,则∠DAE= .
14.如图,已知,,,和的平分线交于,和的平分线交于,和的平分线交于,按如此方式继续下去,用,的代数式表示的度数为 .
15.如图,在中,,是高,是中线,是角平分线,交于点,交于点,下面说法中正确的序号是 .
的面积等于的面积;;;.
16.在,中,,现将直角顶点按照如图方式叠放,点在直线上方,且,能使有一条边与平行的所有的度数为 .
三、解答题
17.如图,,是的两条高,,求的长.
18.在△ABC中,已知∠B=∠A+10°,∠C=∠B+25°,求∠A的度数.
19.如图,,,,求的度数.
20.在各个内角都相等的多边形中,一个内角等于一个外角的3倍,求这个多边形的边数和它的内角和.
21. 如图,将△ABC向左平移6个单位长度,再向下平移4个单位长度,可以得到△A1B1C1,画出平移后的△A1B1C1
①直接写出△A1B1C1各个顶点的坐标;
②写出S△ABC= ▲ .
22.如图,△ABC中,∠ABC的角平分线与外角∠ACD的平分线交于A1.
(1)如图1,若∠A=70°,则∠A1= .
(2)如图2,四边形ABCD中,∠ABC的角平分线及外角∠DCE的角平分线相交于点F, 若∠A+∠D=230°, 求∠F的度数.
(3)如图3,△ABC中,∠ABC的角平分线与外角∠ACD的角平分线交于A1,若E为BA延长线上一动点,连接EC,∠AEC与∠ACE的角平分线交于点Q ,当E滑动时有下面两个结论:
①∠Q+∠A1的值为定值;
②∠Q-∠A1的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】A
8.【答案】C
9.【答案】360°
10.【答案】a﹣3b+c
11.【答案】
12.【答案】稳定
13.【答案】20°
14.【答案】
15.【答案】
16.【答案】或或
17.【答案】
18.【答案】解:∵∠B=∠A+10°,∠C=∠B+25°,
∴∠C=∠B+25° ,
∵
∴
解得
19.【答案】解:∵,,
∴,
∵,,
∴
20.【答案】解:∵在这个正多边形中,一个内角等于与它相邻的一个外角的3倍,则可设这个内角为x则与它相邻的外角度数为:,
由题意可知:,
解得x=135°,
则与它相邻的外角度数为 45°,
∵360°÷45°=8,
∴这个多边形的边数为8,其内角和为8×135°=1080°.
21.【答案】解:①A(-2,1)B(-3,-3)C(-5,-2);
②
22.【答案】(1)35°
(2)解:如图:
∵BF平分∠ABC,CF平分∠DCE,
∴∠FBC=∠ABC,∠FCE=∠DCE
∴∠F=∠FCE-∠FBC=(∠DCE-∠ABC),
∵∠A+∠D=230°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=130°,
∴∠ABC+(180°-∠DCE)=130°,
∴∠DCE-∠ABC=50°,
∴∠F=(∠DCE-∠ABC)=25°;
(3)解:正确的结论是①,理由如下:
如图:
同(1)可得∠A1=∠BAC,
∵EQ平分∠AEC,CQ平分∠ACE,
∴∠QEC=∠AEC,∠QCE=∠ACE,
∵∠Q=180°-(∠QEC+∠QCE),
∴∠Q=180°-(∠AEC+∠ACE),
∵∠BAC=∠AEC+∠ACE,
∴∠Q=180°-∠BAC,
而∠A1=∠BAC,
∴∠Q+∠A1=180°-∠BAC+∠BAC=180°,
∴∠Q+∠A1的值为定值,①正确,其值是180°.
