初中数学人教版八年级上册 第十一章 三角形 单元测试(含答案)
文档属性
| 名称 | 初中数学人教版八年级上册 第十一章 三角形 单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 402.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 00:00:00 | ||
图片预览





文档简介
第十一章 三角形
一、单选题
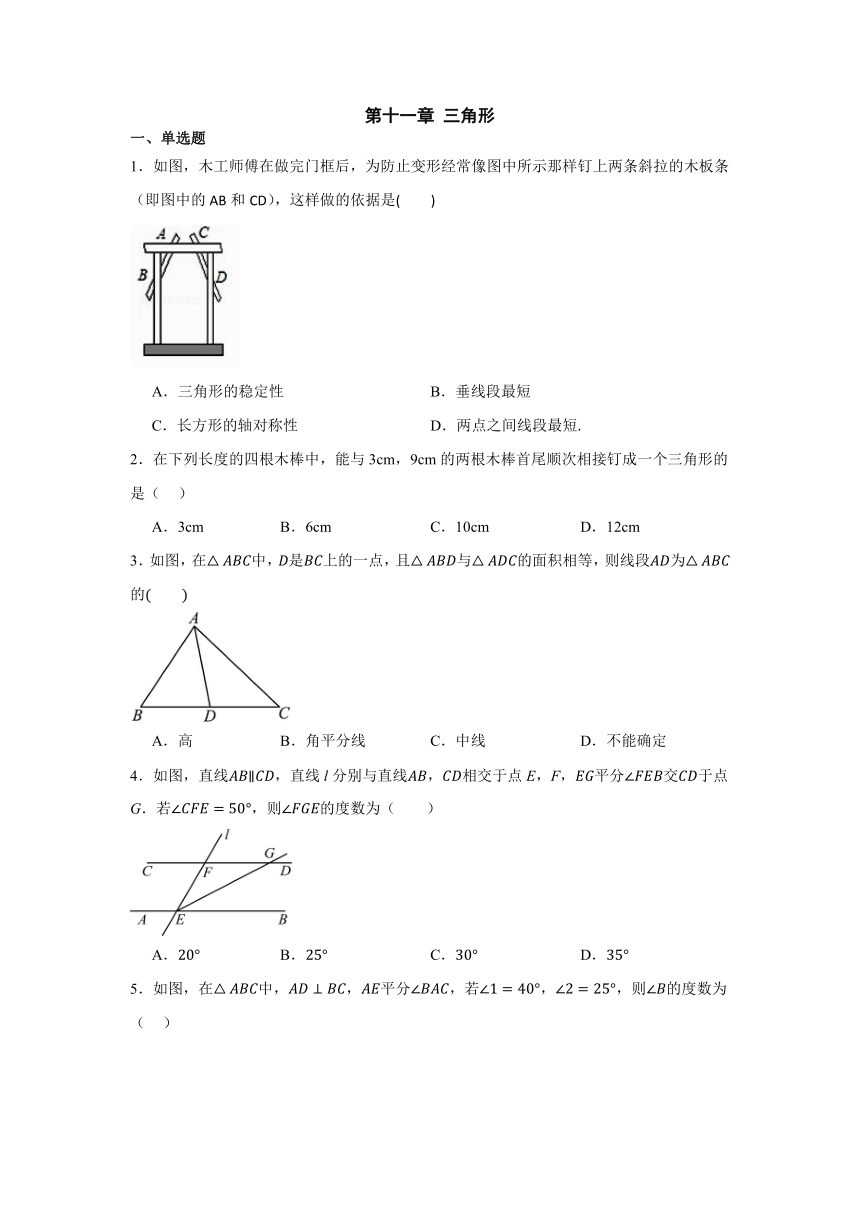
1.如图,木工师傅在做完门框后,为防止变形经常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的依据是( )
A.三角形的稳定性 B.垂线段最短
C.长方形的轴对称性 D.两点之间线段最短.
2.在下列长度的四根木棒中,能与3cm,9cm的两根木棒首尾顺次相接钉成一个三角形的是( )
A.3cm B.6cm C.10cm D.12cm
3.如图,在中,是上的一点,且与的面积相等,则线段为的
A.高 B.角平分线 C.中线 D.不能确定
4.如图,直线,直线l分别与直线相交于点E,F,平分交于点G.若,则的度数为( )
A. B. C. D.
5.如图,在中,,平分,若,,则的度数为( )
A. B. C. D.
6.将一块三角板和一把直尺按如图所示摆放,若,则的度数为( )
A.149° B.139° C.131° D.492°
7.一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是( )
A.17 B.16 C.15 D.16或15或17
8.如图所示,七边形中,的延长线相交于点O,若图中的和为,则的度数为( )
A. B. C. D.
9.如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F,若△ABC的面积为10,则△ADF与△CEF的面积之差是( )
A.5 B.4 C.3.5 D.3
10.如图,的高、相交于点O,下列说法中错误的是( )
A. B.
C. D.
二、填空题
11.△ABC两边a=3,b=6,则第三边c的取值范围为 .
12.在中,,,则 .
13.一个多边形剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为 .
14.如图,含30°角的直角三角板的直角顶点C落在直尺下边沿上,60°角的顶点A落在直尺上边沿,直角边CD与直尺上边沿交于点B.若∠1=33°,则∠2= .
15.如图,是的中线,,若的周长比的周长大,则的长为 .
16.如图是螳螂的示意图,已知,,,则的度数为 .
17.如图,△ABC中,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=120°,∠BGC=102°,则∠A的度数为
18.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1= ;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为 .
三、解答题
19.已知的两边长为,
(1)求的取值范围;
(2)若的周长为偶数,求的长;
20.已知一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半,求这个多边形的内角和.
21.如图,在中,是高,是角平分线,若,,求的度数.
22.如图,在中,,的外角的平分线交的延长线于点E.
(1)补全图形;
(2)求的度数;
(3)已知F为延长线上一点,连接,若,请判断与的位置关系为________.
23.旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相部的两个外角的和之间存在怎样的数量关系呢?
(1)尝试探究:如(图),与分别为的两个外角,试探究与之间存在怎样的数量关系?为什么?
(2)初步应用:如(图),在纸片中剪去得到四边形,,则______;
(3)初步应用:小明联想到了曾经解决的一个问题:如图,在中,、分别平分外角、,与有何数量关系直接写出结论.
参考答案:
1.A
2.C
3.C
4.B
5.B
6.C
7.D
8.D
9.D
10.D
11.
12.30°
13.15,16或17
14.63°
15.
16.
17.42°
18. 32 6
19.(1)解:∵的两边长为,
∴,即;
(2)解:由(1)可得,,
∵的值为7、8、9,
∴(舍),
,
(舍),
∴.
20.设外角为a,则内角为,
∴,
解得:,
∴这个多边形的边数为:,
∴内角和为:.
∴这个多边形的内角和为
21.解: 为高,,
,
,
,
是角平分线,
,
,
的度数为.
22.解:(1)根据题意作图如下:
(2)在中,,,
,
.
是的平分线,
;
(3),理由如下;
,,
.
又,
,
.
23.(1)解:如图中,
;
(2)解:如图中,
,
,
.
(3)解:如图中,
,分别是外角,的平分线,
,
在中,.
一、单选题
1.如图,木工师傅在做完门框后,为防止变形经常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的依据是( )
A.三角形的稳定性 B.垂线段最短
C.长方形的轴对称性 D.两点之间线段最短.
2.在下列长度的四根木棒中,能与3cm,9cm的两根木棒首尾顺次相接钉成一个三角形的是( )
A.3cm B.6cm C.10cm D.12cm
3.如图,在中,是上的一点,且与的面积相等,则线段为的
A.高 B.角平分线 C.中线 D.不能确定
4.如图,直线,直线l分别与直线相交于点E,F,平分交于点G.若,则的度数为( )
A. B. C. D.
5.如图,在中,,平分,若,,则的度数为( )
A. B. C. D.
6.将一块三角板和一把直尺按如图所示摆放,若,则的度数为( )
A.149° B.139° C.131° D.492°
7.一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是( )
A.17 B.16 C.15 D.16或15或17
8.如图所示,七边形中,的延长线相交于点O,若图中的和为,则的度数为( )
A. B. C. D.
9.如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F,若△ABC的面积为10,则△ADF与△CEF的面积之差是( )
A.5 B.4 C.3.5 D.3
10.如图,的高、相交于点O,下列说法中错误的是( )
A. B.
C. D.
二、填空题
11.△ABC两边a=3,b=6,则第三边c的取值范围为 .
12.在中,,,则 .
13.一个多边形剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为 .
14.如图,含30°角的直角三角板的直角顶点C落在直尺下边沿上,60°角的顶点A落在直尺上边沿,直角边CD与直尺上边沿交于点B.若∠1=33°,则∠2= .
15.如图,是的中线,,若的周长比的周长大,则的长为 .
16.如图是螳螂的示意图,已知,,,则的度数为 .
17.如图,△ABC中,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=120°,∠BGC=102°,则∠A的度数为
18.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1= ;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为 .
三、解答题
19.已知的两边长为,
(1)求的取值范围;
(2)若的周长为偶数,求的长;
20.已知一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半,求这个多边形的内角和.
21.如图,在中,是高,是角平分线,若,,求的度数.
22.如图,在中,,的外角的平分线交的延长线于点E.
(1)补全图形;
(2)求的度数;
(3)已知F为延长线上一点,连接,若,请判断与的位置关系为________.
23.旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相部的两个外角的和之间存在怎样的数量关系呢?
(1)尝试探究:如(图),与分别为的两个外角,试探究与之间存在怎样的数量关系?为什么?
(2)初步应用:如(图),在纸片中剪去得到四边形,,则______;
(3)初步应用:小明联想到了曾经解决的一个问题:如图,在中,、分别平分外角、,与有何数量关系直接写出结论.
参考答案:
1.A
2.C
3.C
4.B
5.B
6.C
7.D
8.D
9.D
10.D
11.
12.30°
13.15,16或17
14.63°
15.
16.
17.42°
18. 32 6
19.(1)解:∵的两边长为,
∴,即;
(2)解:由(1)可得,,
∵的值为7、8、9,
∴(舍),
,
(舍),
∴.
20.设外角为a,则内角为,
∴,
解得:,
∴这个多边形的边数为:,
∴内角和为:.
∴这个多边形的内角和为
21.解: 为高,,
,
,
,
是角平分线,
,
,
的度数为.
22.解:(1)根据题意作图如下:
(2)在中,,,
,
.
是的平分线,
;
(3),理由如下;
,,
.
又,
,
.
23.(1)解:如图中,
;
(2)解:如图中,
,
,
.
(3)解:如图中,
,分别是外角,的平分线,
,
在中,.
