初中数学人教版八年级上册 第十三章 轴对称单元测试(含答案)
文档属性
| 名称 | 初中数学人教版八年级上册 第十三章 轴对称单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 520.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 15:15:35 | ||
图片预览




文档简介
第十三章 轴对称
一、单选题
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.若点A(a,-1)与点B(-5,b)关于x轴对称,则a+b=( )
A.5 B.﹣5 C.﹣4 D.4
3.如图,在的边BC所在直线上找一点P,使得为等腰三角形,则满足条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
4.等腰三角形有两条边的长分别为3和4,则该三角形的周长为( )
A.10 B.10或11 C.11 D.7或11
5.如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
6.如图,在中,,点D在上,且,则的度数是( )
A.36° B.45° C.54° D.72°
7.如图,在中,,,点,分别是图中所作直线和射线与,的交点.根据图中尺规作图的痕迹推断,以下结论错误的是( )
A. B.
C. D.
8.如图,为等边三角形,且与相交于点,则( ).
A.等于 B.等于 C.等于 D.大小不确定
9.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.5 B.6 C.7 D.8
10.如图,已知,平分,,在上,在上,在上.当取最小值时,此时的度数为( )
A. B. C. D.
二、填空题
11.已知点A(x,-4)与点B(6,y)关于x轴对称,那么x+y的值为 .
12.如图,这是小明在平面镜里看到的背后墙上电子钟显示的时间,则此刻的实际时间应该是 .
13.等腰三角形两腰上的高所在直线相交所成的锐角为80°,则顶角的度数为 .
14.如图,将△ABC纸片沿DE折叠,使点A落在四边形BCED外点A1的位置,若∠1+∠2=240°,则∠A= °.
15.在边长为3的等边△ABC的AB边上任取一点D,作DF⊥AC交AC于F,在BC的延长线上截取CE=AD,连接DE交AC于G,则FG的值为 .
16.如图所示,已知BO平分∠CBA,CO平分∠ACB,过O点的直线MN∥BC,若AB=12,AC=14,BC=15,则△AMN的周长为 .
17.如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB的平分线,且交AD于P点.如果AP=2,则AB的长为 .
18.如图,等边△ABC的边长为6,AD是高,F是边AB上一动点,E是AD上一动点,则BE+EF的最小值为 .
三、解答题
19.如图,在等腰△ABC中,两条腰上的高BD和CE相交于O,问:△BOC是等腰三角形吗 为什么
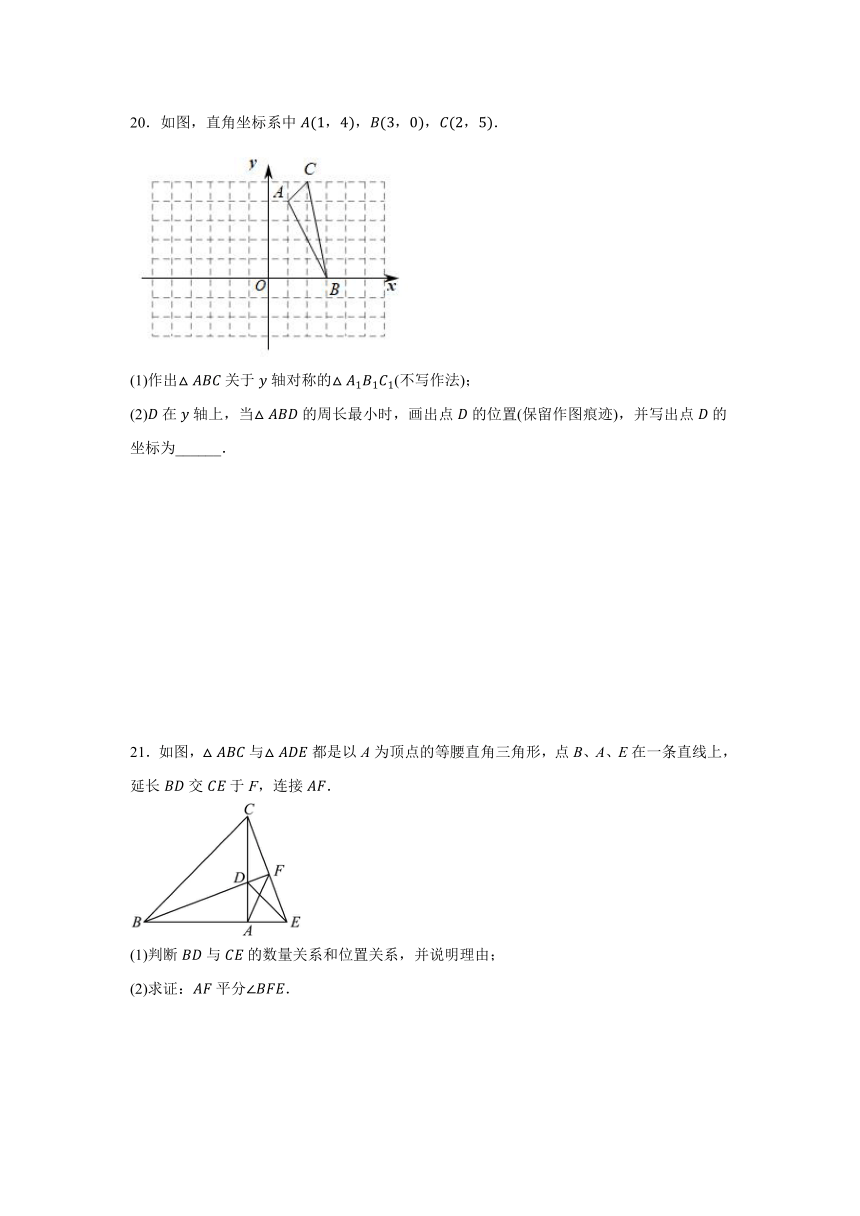
20.如图,直角坐标系中.
(1)作出关于轴对称的(不写作法);
(2)在轴上,当的周长最小时,画出点的位置(保留作图痕迹),并写出点的坐标为______.
21.如图,与都是以A为顶点的等腰直角三角形,点B、A、E在一条直线上,延长交于F,连接.
(1)判断与的数量关系和位置关系,并说明理由;
(2)求证:平分.
22.如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,AE平分∠BAD,交BC于E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使得BM=2DE,连接ME
①求证:ME⊥BC;
②求∠EMC的度数.
23.探究等边三角形“手拉手”问题.
(1)如图1,已如△ABC,△ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE,试判断CE与BA的位置关系,并说明理由;
(2)如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,则∠ADB+∠ADE=________度;
(3)如图3,已知点E在等边三角形△ABC外,点E、点B位于线段AC的异侧,连接BE、CE.若∠BEC=60°,猜想线段BE、AE、CE三者之间的数量关系,并说明理由.
24.如图,在边长为12cm的等边中,P、Q两点分别从点A、点B同时出发,沿三角形的边顺时针方向运动,已知点P的速度为1cm/s,点Q的速度为2cm/s.当点Q第一次到达A点时,P、Q同时停止运动.设运动时间为t秒.求:
(1)用含t的代数式表示_______.
(2)是否存在t,使得为等边三角形.若存在,请求出t的值;若不存在,请说明理由.
(3)是否存在t,使得为直角三角形.若存在,请求出t的值;若不存在,请说明理由.(提示:在直角三角形中,30°角所对的直角边为斜边的一半)
参考答案:
1.B
2.C
3.C
4.B
5.B
6.A
7.D
8.B
9.A
10.D
11.10
12.
13.100°或80°.
14.30
15.
16.26
17.6
18.
19.△OBC是等腰三角形,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
又∵BD⊥AC,CE⊥AB,
∴∠BDC=∠BEC=90°,
∴∠ABC+∠BCE=90°,∠ACB+∠DBC=90°,
∴∠BCE=∠DBC,
即∠OBC=∠OCB,
∴△OBC是等腰三角形.
20.(1)如图所示,即为所求;
(2)如图所示,点即为所求,
∵,
当且仅当三点共线时,的周长最小,
观察坐标系,可知.
21.(1)解:,,理由如下:
在与中,
,
∴,
∴ ,
∵,
∴,
∴,即;
(2)证明:作于G,作于H,如图,
∵,
∴,
∴平分.
22.(1)证明:∵△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵FC⊥BC,
∴∠ACF+∠ACB=90°,
∴∠ACF=45°=∠ABE.
∵∠BAC=90°,FA⊥AE,
∴∠BAE+∠EAC=90°=∠CAF+∠EAC,
∴∠BAE=∠CAF.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
∴BE=CF.
(2)①证明:过点E作EQ⊥AB于点Q,如图所示.
∵AE平分∠BAD,
∴∠QAE=∠DAE,
在△AEQ和△AED中,
,
∴△AEQ≌△AED(AAS),
∴QE=DE.
∵∠BQE=90°,∠QBE=45°,
∴∠BEQ=45°,
∴BQ=QE,
又∵BM=2DE=QE,
∴QM=QE,
∴∠QEM=∠QME==45°,
∴∠BEM=∠BEQ+∠QEM=90°,
∴ME⊥BC.
②设DE=a,则BM=2a.
∵△BEM为等腰直角三角形,
∴BE=EM=BM=a,
∴BD=BE+DE=(+1)a.
∵△ABC为等腰直角三角形,AD⊥BC,
∴AB=BD=×(+1)a=(2+)a,
∵BM=2a,
∴AM=(2+)a-2a=a,
∴AM=EM.
在Rt△MAC和Rt△MEC中,
,
∴Rt△MAC≌Rt△MEC(HL),
∴∠EMC=∠AMC,
又∵∠BME=45°,
∴∠EMC=(180°-45°)=67.5°
23.(1)解:结论:CE//AB.
理由:如图1中,∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE=60°,
∴∠BAC=∠ACE=60°,
∴AB//CE.
(2)证明:如图2中,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC,
∵△ADE是等边三角形,
∴∠AED=∠ADE=60°,
∵∠BEC=60°,
∴∠AEC=∠AED+∠BEC=120°,
∴∠ADB=∠AEC=120°,
∴∠ADB+∠ADE=120°+60°=180°,
(2)结论:BE=AE+EC.
理由:在线段BE上取一点H,使得BH=CE,设AC交BE于点O.
∵△ABC是等边三角形,
∴AB=BC,∠BAC=60°,
∵∠BEC=60°,
∴∠BAO=∠OEC=60°,
∵∠AOB=∠EOC,
∴∠ABH=∠ACE,
∵BA=CA,BH=CE,
∴△ABH≌△ACE(SAS)
∴∠BAH=∠CAE,AH=AE,
∴∠HAE=∠BAC=60°,
∴△AEH是等边三角形,
∴AE=EH,
∴BE=BH+EH=EC+AE,
即BE=AE+EC.
24.(1)解:点Q的速度为2cm/s, ,
故答案为:
(2)是等边三角形,
当时,是等边三角
解得
(3)①当时,如图,
即
解得
②当时候,如图
即
解得
综上所述,当或时,为直角三角形
一、单选题
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.若点A(a,-1)与点B(-5,b)关于x轴对称,则a+b=( )
A.5 B.﹣5 C.﹣4 D.4
3.如图,在的边BC所在直线上找一点P,使得为等腰三角形,则满足条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
4.等腰三角形有两条边的长分别为3和4,则该三角形的周长为( )
A.10 B.10或11 C.11 D.7或11
5.如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
6.如图,在中,,点D在上,且,则的度数是( )
A.36° B.45° C.54° D.72°
7.如图,在中,,,点,分别是图中所作直线和射线与,的交点.根据图中尺规作图的痕迹推断,以下结论错误的是( )
A. B.
C. D.
8.如图,为等边三角形,且与相交于点,则( ).
A.等于 B.等于 C.等于 D.大小不确定
9.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.5 B.6 C.7 D.8
10.如图,已知,平分,,在上,在上,在上.当取最小值时,此时的度数为( )
A. B. C. D.
二、填空题
11.已知点A(x,-4)与点B(6,y)关于x轴对称,那么x+y的值为 .
12.如图,这是小明在平面镜里看到的背后墙上电子钟显示的时间,则此刻的实际时间应该是 .
13.等腰三角形两腰上的高所在直线相交所成的锐角为80°,则顶角的度数为 .
14.如图,将△ABC纸片沿DE折叠,使点A落在四边形BCED外点A1的位置,若∠1+∠2=240°,则∠A= °.
15.在边长为3的等边△ABC的AB边上任取一点D,作DF⊥AC交AC于F,在BC的延长线上截取CE=AD,连接DE交AC于G,则FG的值为 .
16.如图所示,已知BO平分∠CBA,CO平分∠ACB,过O点的直线MN∥BC,若AB=12,AC=14,BC=15,则△AMN的周长为 .
17.如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB的平分线,且交AD于P点.如果AP=2,则AB的长为 .
18.如图,等边△ABC的边长为6,AD是高,F是边AB上一动点,E是AD上一动点,则BE+EF的最小值为 .
三、解答题
19.如图,在等腰△ABC中,两条腰上的高BD和CE相交于O,问:△BOC是等腰三角形吗 为什么
20.如图,直角坐标系中.
(1)作出关于轴对称的(不写作法);
(2)在轴上,当的周长最小时,画出点的位置(保留作图痕迹),并写出点的坐标为______.
21.如图,与都是以A为顶点的等腰直角三角形,点B、A、E在一条直线上,延长交于F,连接.
(1)判断与的数量关系和位置关系,并说明理由;
(2)求证:平分.
22.如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,AE平分∠BAD,交BC于E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使得BM=2DE,连接ME
①求证:ME⊥BC;
②求∠EMC的度数.
23.探究等边三角形“手拉手”问题.
(1)如图1,已如△ABC,△ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE,试判断CE与BA的位置关系,并说明理由;
(2)如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,则∠ADB+∠ADE=________度;
(3)如图3,已知点E在等边三角形△ABC外,点E、点B位于线段AC的异侧,连接BE、CE.若∠BEC=60°,猜想线段BE、AE、CE三者之间的数量关系,并说明理由.
24.如图,在边长为12cm的等边中,P、Q两点分别从点A、点B同时出发,沿三角形的边顺时针方向运动,已知点P的速度为1cm/s,点Q的速度为2cm/s.当点Q第一次到达A点时,P、Q同时停止运动.设运动时间为t秒.求:
(1)用含t的代数式表示_______.
(2)是否存在t,使得为等边三角形.若存在,请求出t的值;若不存在,请说明理由.
(3)是否存在t,使得为直角三角形.若存在,请求出t的值;若不存在,请说明理由.(提示:在直角三角形中,30°角所对的直角边为斜边的一半)
参考答案:
1.B
2.C
3.C
4.B
5.B
6.A
7.D
8.B
9.A
10.D
11.10
12.
13.100°或80°.
14.30
15.
16.26
17.6
18.
19.△OBC是等腰三角形,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
又∵BD⊥AC,CE⊥AB,
∴∠BDC=∠BEC=90°,
∴∠ABC+∠BCE=90°,∠ACB+∠DBC=90°,
∴∠BCE=∠DBC,
即∠OBC=∠OCB,
∴△OBC是等腰三角形.
20.(1)如图所示,即为所求;
(2)如图所示,点即为所求,
∵,
当且仅当三点共线时,的周长最小,
观察坐标系,可知.
21.(1)解:,,理由如下:
在与中,
,
∴,
∴ ,
∵,
∴,
∴,即;
(2)证明:作于G,作于H,如图,
∵,
∴,
∴平分.
22.(1)证明:∵△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵FC⊥BC,
∴∠ACF+∠ACB=90°,
∴∠ACF=45°=∠ABE.
∵∠BAC=90°,FA⊥AE,
∴∠BAE+∠EAC=90°=∠CAF+∠EAC,
∴∠BAE=∠CAF.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
∴BE=CF.
(2)①证明:过点E作EQ⊥AB于点Q,如图所示.
∵AE平分∠BAD,
∴∠QAE=∠DAE,
在△AEQ和△AED中,
,
∴△AEQ≌△AED(AAS),
∴QE=DE.
∵∠BQE=90°,∠QBE=45°,
∴∠BEQ=45°,
∴BQ=QE,
又∵BM=2DE=QE,
∴QM=QE,
∴∠QEM=∠QME==45°,
∴∠BEM=∠BEQ+∠QEM=90°,
∴ME⊥BC.
②设DE=a,则BM=2a.
∵△BEM为等腰直角三角形,
∴BE=EM=BM=a,
∴BD=BE+DE=(+1)a.
∵△ABC为等腰直角三角形,AD⊥BC,
∴AB=BD=×(+1)a=(2+)a,
∵BM=2a,
∴AM=(2+)a-2a=a,
∴AM=EM.
在Rt△MAC和Rt△MEC中,
,
∴Rt△MAC≌Rt△MEC(HL),
∴∠EMC=∠AMC,
又∵∠BME=45°,
∴∠EMC=(180°-45°)=67.5°
23.(1)解:结论:CE//AB.
理由:如图1中,∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE=60°,
∴∠BAC=∠ACE=60°,
∴AB//CE.
(2)证明:如图2中,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC,
∵△ADE是等边三角形,
∴∠AED=∠ADE=60°,
∵∠BEC=60°,
∴∠AEC=∠AED+∠BEC=120°,
∴∠ADB=∠AEC=120°,
∴∠ADB+∠ADE=120°+60°=180°,
(2)结论:BE=AE+EC.
理由:在线段BE上取一点H,使得BH=CE,设AC交BE于点O.
∵△ABC是等边三角形,
∴AB=BC,∠BAC=60°,
∵∠BEC=60°,
∴∠BAO=∠OEC=60°,
∵∠AOB=∠EOC,
∴∠ABH=∠ACE,
∵BA=CA,BH=CE,
∴△ABH≌△ACE(SAS)
∴∠BAH=∠CAE,AH=AE,
∴∠HAE=∠BAC=60°,
∴△AEH是等边三角形,
∴AE=EH,
∴BE=BH+EH=EC+AE,
即BE=AE+EC.
24.(1)解:点Q的速度为2cm/s, ,
故答案为:
(2)是等边三角形,
当时,是等边三角
解得
(3)①当时,如图,
即
解得
②当时候,如图
即
解得
综上所述,当或时,为直角三角形
